Transport of H2S and HS− across the human red blood cell membrane: rapid H2S diffusion and AE1-mediated Cl−/HS− exchange (original) (raw)

Abstract

The rates of H2S and HS− transport across the human erythrocyte membrane were estimated by measuring rates of dissipation of pH gradients in media containing 250 μM H2S/HS−. Net acid efflux is caused by H2S/HS− acting analogously to CO2/HCO3− in the Jacobs-Stewart cycle. The steps are as follows: 1) H2S efflux through the lipid bilayer and/or a gas channel, 2) extracellular H2S deprotonation, 3) HS− influx in exchange for Cl−, catalyzed by the anion exchange protein AE1, and 4) intracellular HS− protonation. Net acid transport by the Cl−/HS−/H2S cycle is more efficient than by the Cl−/HCO3−/CO2 cycle because of the rapid H2S-HS− interconversion in cells and medium. The rates of acid transport were analyzed by solving the mass flow equations for the cycle to produce estimates of the HS− and H2S transport rates. The data indicate that HS− is a very good substrate for AE1; the Cl−/HS− exchange rate is about one-third as rapid as Cl−/HCO3− exchange. The H2S permeability coefficient must also be high (>10−2 cm/s, half time <0.003 s) to account for the pH equilibration data. The results imply that H2S and HS− enter erythrocytes very rapidly in the microcirculation of H2S-producing tissues, thereby acting as a sink for H2S and lowering the local extracellular concentration, and the fact that HS− is a substrate for a Cl−/HCO3− exchanger indicates that some effects of exogenous H2S/HS− may not result from a regulatory role of H2S but, rather, from net acid flux by H2S and HS− transport in a Jacobs-Stewart cycle.

Keywords: hydrogen sulfide, sulfide anion, AE1, transport, erythrocyte

there is considerable evidence for the importance of H2S as a signaling molecule, especially in the cardiovascular and nervous systems. Mammalian cells undoubtedly can produce H2S (40, 67), and it is equally clear that exogenous H2S/HS− has effects on a variety of biological systems (1, 25, 41, 54, 68, 75). However, there are very wide variations in estimates of circulating H2S levels in mammals (56, 71), and much remains to be learned about the conditions under which endogenously produced H2S has significant physiological effects (50).

An understanding of the cellular physiology of H2S requires quantitative information on the transport of H2S, as well as HS−, which, at neutral or alkaline pH, is present at a higher concentration than H2S [p_K_a = 6.76 at 37°C (26)]. Two recent studies have provided strong evidence for rapid H2S diffusion through lipid bilayers. Mathai et al. (46) measured pH changes associated with H2S diffusion across planar lipid bilayers and found that the permeability coefficient for H2S is ≥0.5 cm/s. Cuevasanta et al. (7) showed that the lipid-water partition coefficient of H2S is ∼2, which is consistent with a bilayer permeability coefficient of 3 cm/s. The time course of H2S transport in liposomes is too fast to measure with stopped flow, indicating that the permeability coefficient is >1 cm/s (7). The permeability of lipid bilayers to HS− has not been measured but is undoubtedly orders of magnitude lower than that of H2S, as is true of other weak acids and their respective anions (58).

Although it is clear that the H2S permeability of lipid bilayers is quite high, there have been relatively few measurements of H2S and/or HS− transport in biological systems; these are summarized briefly below.

In 1936, Jacques (28) measured the influx of H2S in the alga Valonia macrophysa and found that the half time for influx was ∼5 min. If V. macrophysa is modeled as a sphere of 1-cm radius, the influx half time corresponds to a permeability coefficient of 8 × 10−4 cm/s. This permeability is orders of magnitude lower than the above estimates for lipid bilayers, but influx in these very large cells could be limited in part by unstirred layers.

Julian and Arp (33) determined the H2S and HS− permeabilities of the body wall and hindgut of the marine worm Urechis caupo and found that the H2S permeability is only moderately higher than that of HS−. The highest permeability coefficient was for H2S permeation of stretched hindgut (5 × 10−4 cm/s). Again, this permeability coefficient is orders of magnitude lower than that of lipid bilayers; as in Valonia, diffusional barriers other than cell membranes may contribute to the low permeability.

The hydrothermal vent tubeworm Riftia pachyptila takes up H2S/HS− from the environment for the purpose of supplying H2S for oxidation by symbiotic intracellular bacteria. Goffredi et al. (17) found that, surprisingly, H2S diffusion into R. pachyptila is slower than expected and that HS− influx is the more important mechanism of H2S acquisition. Another tubeworm, Lammelibrachia, acquires H2S through its root; the permeability coefficient for H2S/HS− transport through the root tube wall of this species is ∼10−3 cm/s for the thinnest walls (34). There is no significant effect of pH on influx, indicating that H2S and HS− have roughly equal permeabilities. In contrast, the pH dependence of the toxicity of H2S/HS− in the shrimp Crangon crangon indicates that H2S is the main species that enters the organism (66).

Czyzewski and Wang (8) recently identified a protein in Clostridium difficile that transports HS−. The protein is a member of the formate/NO2− transporter family. The transport of HS− through this protein was not measured directly, but formate transport measurements showed that the influx of formate is inhibited by low (<1 mM) concentrations of HS−. Moreover, HS− increases the thermostability of the detergent-solubilized protein, indicating that HS− binds to the transporter with higher affinity than formate, Cl−, or NO2−.

In summary, published information on H2S and HS− transport is limited to lipid bilayers, bacteria, algae, and marine invertebrates. The experiments described here use the human erythrocyte as a system for obtaining quantitative information on the rates of H2S and HS− transport in a mammalian cell at physiological pH and temperature. The results show that H2S and HS− can mediate the transport of acid equivalents across the erythrocyte membrane by a process analogous to the Jacobs-Stewart cycle for Cl−, HCO3−, and CO2 (27). In fact, H2S and HS− are even more efficient than CO2 and HCO3− in the Jacobs-Stewart cycle, because the p_K_a of H2S is close to neutrality, and H2S/HS− protonation and deprotonation do not require hydration and dehydration. The data indicate that H2S and HS− are transported very rapidly. The H2S permeability coefficient at 37°C is ≥0.01 cm/s. In addition, HS− is a very good substrate for the anion exchange protein AE1. The only anions that can exchange with Cl− more rapidly than HS− are Cl−, HCO3−, and NO3−. The implications of these findings for the interpretation of exogenous H2S experiments and for the disposition of endogenous H2S are discussed.

MATERIALS AND METHODS

Materials

The study was approved by the Institutional Review Board of the University of Arkansas for Medical Sciences, and written informed consent was obtained from the study participants. Human blood was obtained from hematologically healthy donors in the laboratory of Jerry Ware (Department of Physiology and Biophysics). Blood was drawn by venipuncture into heparin and stored as packed cells in plasma for ≤6 days at 4°C. H2DIDS was synthesized from 4,4′-diaminostilbene-2,2′-disulfonate (Eastman Chemicals), as described previously (31). Ethoxzolamide was purchased from Sigma-Aldrich and added to cell suspensions from a 10 mM stock solution in ethanol. All salts and buffers were obtained from Thermo-Fisher or Sigma-Aldrich.

Methods

Cells were washed three times in unbuffered 160 mM KCl and resuspended at 8% hematocrit in 160 mM KCl buffered with 1 mM glycylglycine and 0.5 mM HEPES hemisodium. The suspension (20 ml) was stirred at 37°C in a 40-ml tube exposed to room air, unless otherwise indicated. The extracellular pH (pHo) of the suspension was measured continuously with a glass combination electrode (catalog no. 13-620-285, Fisher) and a pH meter (Fisher). The analog output of the pH meter was digitized at a rate of 4 s−1 with an AEMC data logger (CAS Data Loggers, Chesterland, OH) and stored as an Excel file. NaHCO3 was added to bring the solution close to equilibrium with atmospheric CO2 (currently 400 ppm; http://www.esrl.noaa.gov/gmd/ccgg/trends/), resulting in ∼9.3 μM dissolved CO2 and ∼186 μM dissolved HCO3− at pH 7.4 and 37°C. For experiments at equilibrium pHo >7.4, the suspensions were titrated to the desired pHo by addition of aliquots of NaOH and Na2CO3.

Extracellular buffer power (μeq/pH) was determined by measuring the change in pHo caused by addition of 1-μmol aliquots of HCl or NaOH to the suspension in the presence of H2DIDS, which inhibits pH equilibration across the red cell membrane. The extracellular buffer power was about one-eighth of the intracellular buffer power (see below). Addition of 5 μmol of NaOH raised the equilibrium pHo of the suspension by ∼0.05 unit. Since the extracellular buffer power was only a small fraction of the total buffer power, pHo initially increased by ∼0.35 unit and then decreased to the new equilibrium pHo as acid exited the cells. For small departures from the final equilibrium pH, the time course of approach to equilibrium was not distinguishable from a single exponential. The rate constant for pH equilibration (_k_pH, min−1) was determined from nonlinear regression of pH vs. time curves over the pH range 0.07–0.02 from the final value using Sigma Plot 12 (Systat Software) with the default settings. The _r_2 values for the regressions were always >0.99.

Intracellular buffer power was estimated as follows. The change in equilibrium pHo resulting from addition of 5 μmol of HCl or NaOH was measured. The change in equilibrium intracellular pH (pHi) is ∼80% of the change in pHo in the range close to pH 7.4 (61). From the change in pHi and the known amount of acid or base that entered the cells, an intracellular buffer power of 65–69 μeq/ml cells-pH (n = 3) was estimated at pHo 7.4. This value is ∼20% higher than that estimated by Harris and Maizels (24) on erythrocyte lysates and 20% lower than the recent estimate by Swietach et al. (61) on intact cells using ammonium pulses. The uncertainty in the absolute value of the buffer power of red cell cytosol does not have a significant effect on the interpretation of these experiments, because the rate of change of pHo depends mainly on the extracellular buffer power.

Modeling

The Jacobs-Stewart cycle consists of the following four steps for net acid efflux (Fig. 1). The total net mass flow (nmol/s) for each of the steps can be expressed in terms of the ion concentrations, intracellular and extracellular water volumes, and rate parameters for transport and protonation/deprotonation.

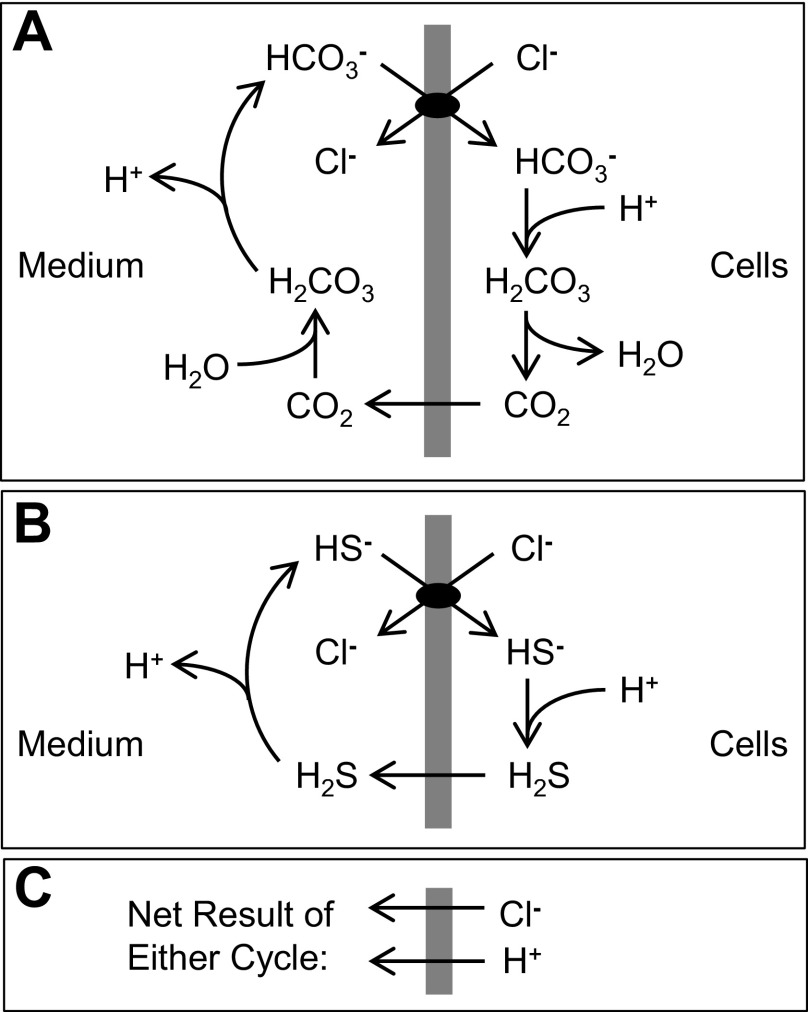
Fig. 1.

Fig. 1.

A: Jacobs-Stewart cycle for net efflux of acid. Starting at the top and going clockwise, the steps are as follows: 1) Cl−/HCO3− exchange, 2) intracellular HCO3− protonation and dehydration, 3) CO2 efflux, and 4) extracellular CO2 hydration and deprotonation. B: Jacobs-Stewart cycle for net efflux of acid mediated by Cl−/HS− exchange, intracellular HS− protonation, H2S efflux, and extracellular H2S deprotonation. C: net result of 1 cycle.

Step 1: exchange of extracellular anionic base (HCO3− or HS−) for intracellular Cl−.

net mass flow=Vckex(rCl[B−]o−[B−]i) (1)

where Vc is the volume of cell water (ml), _k_ex is the unimolecular rate constant (s−1) for Cl−/B− exchange (where B− is anionic base), [B−]o and [B−]i are extracellular and intracellular B− concentrations (μM), respectively, and rCl is the Donnan ratio ([Cl−]i/[Cl−]o) for the final equilibrium state (where [Cl−]i and [Cl−]o represent intracellular and extracellular Cl− concentration, respectively). The rate constant for exchange, _k_ex, is a lumped parameter that depends on the number of copies of AE1 per cell, the cell surface-to-volume ratio, the substrate ion concentrations, substrate binding affinities, and the translocation rate constants, which are in general asymmetric (14, 37). Even though the values of the true affinities and translocation rate constants are not known accurately, a reasonable empirical estimate for _k_ex for Cl−/HCO3− exchange is ∼8 s−1 at pH 7.4 and 37°C (5, 72). The _k_ex for Cl−/HS− exchange is unknown and is estimated below (see discussion).

Step 2: protonation of intracellular base B− (HCO3− or HS−) to acid HB (CO2 or H2S).

net mass flow=Vc(koni[B−]i[H+]i−koffi[HB]i) (2)

All concentration units are μM, and the units of the forward rate constant (_k_oni) are μM−1·s−1. The rate of protonation of HS− in water is very likely diffusion-limited; _k_oni is assumed to be 1010 M−1·s−1, or 104 μM−1·s−1 (10, 57). With this association rate constant and the p_K_a of 6.76 at 37°C (26), the H2S dissociation rate constant (_k_offi) is 1,738 s−1.

For HCO3−/CO2, in the absence of catalyst, the effective H+ dissociation rate constant is the unimolecular rate constant for the reaction CO2 + H2O → HCO3− + H+, which is 0.15/s at 37°C (43). The rate constant for the reverse reaction, HCO3− + H+ → CO2 + H2O, is 1.89 × 105 M−1·s−1 = 0.189 μM−1·s−1 (43). In erythrocyte cytosol, which has very high carbonic anhydrase activity, the forward and reverse rate constants are assumed to be 20,000-fold higher than the rate constants without catalyst (13, 44, 45, 73).

Step 3: efflux of acid (CO2 or H2S) driven by the concentration gradient.

net mass flow=VcPA(Ac/Vc)([HB]i−[HB]o) (3)

where _P_A (cm/s) is the permeability coefficient for the acid (CO2 or H2S), Vc is total cell water volume (ml), _A_c/Vc is the cell surface area-to-water volume ratio (2.22 × 104 cm−1), and the concentration units are μM (nmol/ml). _P_A for CO2 is assumed to be 0.12 cm/s (13). (For estimates of _P_A for H2S, see discussion.)

Step 4: deprotonation of extracellular acid.

net mass flow=Vo(koffo[HB]o−kono[B−]o[H+]o) (4)

where Vo is the volume (ml) of extracellular medium, _k_offo is the unimolecular rate constant (s−1) for deprotonation of extracellular HB, and _k_ono (μM−1·s−1) is the bimolecular rate constant for protonation of extracellular B−. The rate constants for protonation/deprotonation of HS−/H2S are assumed to be the same as the intracellular rate constants (step 2).

For the reaction CO2 + H2O ↔ HCO3− + H+, the forward and reverse rates are assumed to be the uncatalyzed rates (see above) plus the rate catalyzed by carbonic anhydrase IV on the extracellular surface, which is ∼0.2% of the activity of the whole cell (74), plus cytosolic carbonic anhydrase released from lysed cells. The fractional lysis during the measurement of CO2/HCO3−-mediated pH equilibration in Fig. 2 was ∼0.2%, estimated from hemoglobin absorbance of supernatants. In an 8% suspension of erythrocytes, 0.2% lysis plus the 0.2% carbonic anhydrase IV cell surface activity would increase the rate of extracellular CO2/HCO3− hydration/dehydration by 0.004 × 0.08 × 20,000 = 6.4 times the uncatalyzed rate. Therefore, for CO2/HCO3−, the extracellular off and on rate constants are assumed to be ∼7.4 times the uncatalyzed rate constants: _k_offo is assumed to be 0.15 × 7.4 s−1 = 1.11 s−1, and _k_ono is 0.189 × 7.4 = 1.40 μM−1·s−1.

Fig. 2.

Fig. 2.

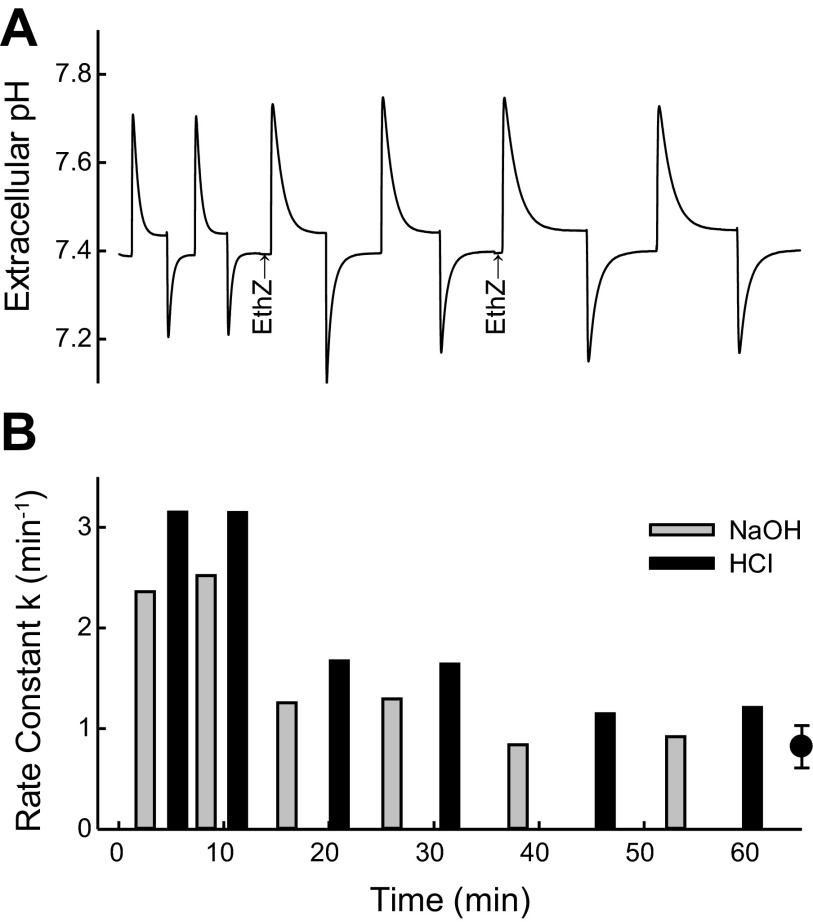
Effect of ethoxzolamide on rate of pH equilibration in human erythrocytes at 37°C and atmospheric CO2. Washed erythrocytes (1.75 ml) were suspended in 160 mM KCl buffered with 1 mM glycylglycine and 0.5 mM HEPES. Extracellular buffer power was 14 μmol/pH, and intracellular buffer power was 115 μmol/pH. A: pH vs. time. Each upstroke of the pH trace represents addition of 5 μmol of NaOH, and each downstroke represents addition of 5 μmol of HCl. Ethoxzolamide (EthZ, 10 μM) was added from a 10 mM stock solution in ethanol at each arrow. Final ethanol concentration was 0.2%. B: rate constants for pH equilibration calculated from pH transients over the range 0.07–0.02 unit from the final value. Point with error bars at right represents mean and range of rates of CO2-independent pH equilibration at pH 7.3–7.5 previously published (29) corrected to 37°C and the extracellular buffer power in the present experiment. Rate of pH equilibration in the presence of 20 μM ethoxzolamide is approximately equal to the CO2-independent rate.

As cells and medium approach a new Donnan equilibrium pH following addition of NaOH or HCl to the medium, the Jacobs-Stewart cycle at any given instant is assumed to be in a steady state, with equal mass flow for all four steps. The equality of mass flow for any two of the above steps can be expressed as three independent equations:

Vckex(rCl[B−]o−[B−]i)=Vc(koni[B−]i[H+]i−koffi[HB]i) (5)
Vc(koni[B−]i[H+]i−koffi[HB]i)=VcPA(Ac/Vc)([HB]i−[HB]o) (6)
VcPA(Ac/Vc)([HB]i−[HB]o)=Vo(koffo[HB]o−kono[B−]o[H+]o) (7)

A fourth equation is conservation of mass (total S or total CO2)

Vc[HB]i+Vc[B−]i+Vo[HB]o+Vo[B−]o=T(nmol) (8)

where T is the total number of nanomoles of B− + HB in the suspension. CO2 and H2S can diffuse between the suspension and atmosphere, but within the relatively short time course of a single pH equilibration transient, T is assumed to be constant.

Equations 5–8 constitute a set of linear equations that can be solved for the four unknown concentrations [HB]i, [B−]i, [HB]o, and [B−]o if the values of all the other parameters are specified. The equations were set up as an augmented matrix in Excel and solved by Gauss-Jordan reduction. Once the values of [HB]i, [B−]i, [HB]o, and [B−]o were solved in terms of pHo, pHi, and values of the other parameters, the net mass flow (nmol/s) was calculated at pHo 0.05 unit above (base pulse) or below (acid pulse) the new equilibrium value. This mass flow was converted to a rate of change of pHo using the measured extracellular buffer power (nmol/pH). From the rate of change of pHo and the difference between pHo and the equilibrium pHo, predicted unimolecular rate constants for pH equilibration (_k_pH, min−1) were calculated for various values of the transport parameters (_k_ex and _P_A) and compared with the measured rate constants (see discussion).

RESULTS

Jacobs-Stewart Cycle in the Presence of Atmospheric CO2

It has been known for many years (9, 15, 24, 65, 69) that mammalian red blood cells and extracellular medium are in general at Gibbs-Donnan equilibrium with respect to Cl−, HCO3−, H+, and OH−:

[Cl−]i/[Cl−]o=[HCO3−]i/[HCO3−]o=[OH−]i/[OH−]o=[H+]o/[H+]i (9)

At 37°C and pHo 7.4 in an isotonic medium (150 mM Cl−), rCl is ∼0.66 (15); as the equilibrium pHo and pHi are raised, the net negative charge on hemoglobin and other impermeant cellular anions increases, and rCl decreases. The intracellular and extracellular concentrations of CO2 are equal, and the Cl−, HCO3−, and H+ concentrations conform to Eq. 9. The cells and medium are normally at Donnan equilibrium because the membrane has a very high rate of Cl−/HCO3− exchange mediated by the anion exchange protein AE1 (36, 53), as well as a high rate of CO2 transport by a combination of diffusion through the lipid bilayer and transport through gas channels (6, 13, 21, 48).

If pHo is suddenly increased by addition of a pulse of NaOH, the equilibrium represented by Eq. 9 is disrupted in two ways: the increased [HCO3−]o creates a driving force for net influx of HCO3− in exchange for Cl−, and the decreased [CO2]o creates a driving force for diffusional CO2 efflux. The combination of HCO3− influx and CO2 efflux results in net acid efflux, which, over time, brings the system to a new Donnan equilibrium.

In the experiments described here, the HCO3− and CO2 concentrations are relatively low, and the intracellular buffer power is ∼67 μeq/ml cells-pH (see Methods). At ∼185 μM HCO3− (equilibrium with atmospheric CO2 at pH 7.4), the number of moles of HCO3− transported in order for AE1-mediated Cl−/HCO3− exchange to reach equilibrium is not, by itself, enough to change pHo or pHi substantially. Instead, the system reaches a new Donnan equilibrium by a repeated cycle (Fig. 1_A_) consisting of HCO3− influx in exchange for Cl−, intracellular HCO3− protonation/dehydration, CO2 efflux, and extracellular CO2 hydration/deprotonation to regenerate HCO3−. One complete cycle results in the net efflux of 1 Cl− and 1 H+. There is also an influx of 1 water molecule per cycle because of extracellular hydration and intracellular dehydration, but this water is more than compensated by osmotic water efflux that follows the net Cl− efflux. Water fluxes are ignored in the analysis of the experiments described here, because the amount of net water transport associated with pH equilibration within a single pH transient is <1% of the total cell water.

The cycle in Fig. 1_A_ was originally described in 1942 by Jacobs and Stewart (27) in connection with net transport of ammonium salts, and the cycle is a general way to transport acid equivalents by transporting CO2 and HCO3− in opposite directions. As illustrated in Fig. 1_B_, H2S and HS− can, in principle, act by analogy to CO2 and HCO3− in the Jacobs-Stewart cycle if H2S and HS− are transported rapidly. Jacobs and Stewart in fact mentioned the possibility of sulfide cycling in their original paper (27).

Before investigating possible H2S/HS− transport, the rate of pH equilibration by the conventional Jacobs-Stewart cycle was measured in the presence of atmospheric CO2. Figure 2_A_ shows the results of acid and base pulses applied to an 8% suspension of human erythrocytes in 160 mM KCl buffered weakly with glycylglycine and HEPES. The total intracellular buffer power was about eight times the extracellular buffer power. Starting at Donnan equilibrium, pHo 7.38, a pulse of NaOH (5 μmol) transiently raised pHo ∼0.3 unit. The pH transient dissipated over the next 2 min with a _k_pH of 2.5 min−1 and final equilibrium pHo ∼0.05 unit higher than initially. A pulse of 5 μmol of HCl returned pHo to ∼7.38 after a transient extracellular acidification. As expected, a second pair of NaOH and HCl pulses resulted in pH transients that dissipated with rates that are very similar to the first. The rate constants for decay of the pH transients are plotted in Fig. 2_B_.

At the time indicated in Fig. 2_A_, the membrane-permeant carbonic anhydrase inhibitor ethoxzolamide (44, 45) was added, and alternating NaOH and HCl pulses were applied. In the presence of 10 μM ethoxzolamide, the pH transients decay with a slower time course. After another addition of 10 μM ethoxzolamide, _k_pH was reduced further to ∼0.8/min. This rate constant is consistent with previously published data on CO2-independent, AE1-mediated pH equilibration, which has the characteristics of H+-Cl− cotransport, rather than Cl−/OH− exchange (29). For the CO2-independent process, _k_pH is slightly higher after an acid pulse than after a base pulse (see discussion). These data confirm that, under these conditions (atmospheric CO2), the Jacobs-Stewart cycle mediates a moderately rapid pH equilibration in human red blood cells; the ethoxzolamide-sensitive _k_pH = 1.5–2 min−1.

H2S/HS− Accelerates pH Equilibration More Than CO2/HCO3− at Similar Concentration

The pH trace in Fig. 3_A_ represents a continuation of that in Fig. 2_A_, beginning with the last pair of base and acid pulses in Fig. 2_A_ (continued presence of atmospheric CO2 and 20 μM ethoxzolamide). Addition of 5 μmol of Na2S (250 μM final) caused immediate alkalinization of the medium, because S2− is an extremely strong base (26) and is rapidly protonated to HS−. Therefore, addition of 5 μmol of Na2S is the equivalent of addition of 5 μmol each of NaOH and NaHS (or 10 μmol of NaOH and 5 μmol of H2S). The pH transient following addition of Na2S decayed much more rapidly than that following NaOH in the absence of H2S/S−, indicating that the cycling of H2S and HS− produces a more rapid rate of pH equilibration than that of CO2/HCO3− under these conditions. The sulfide-dependent _k_pH is ∼4 min−1 (Fig. 3_B_), which is over twice the ethoxzolamide-sensitive rate (Fig. 2), under conditions of approximately equal total amounts of CO2/HCO3− (195 μM) vs. H2S/HS− (250 μM).

Fig. 3.

Fig. 3.

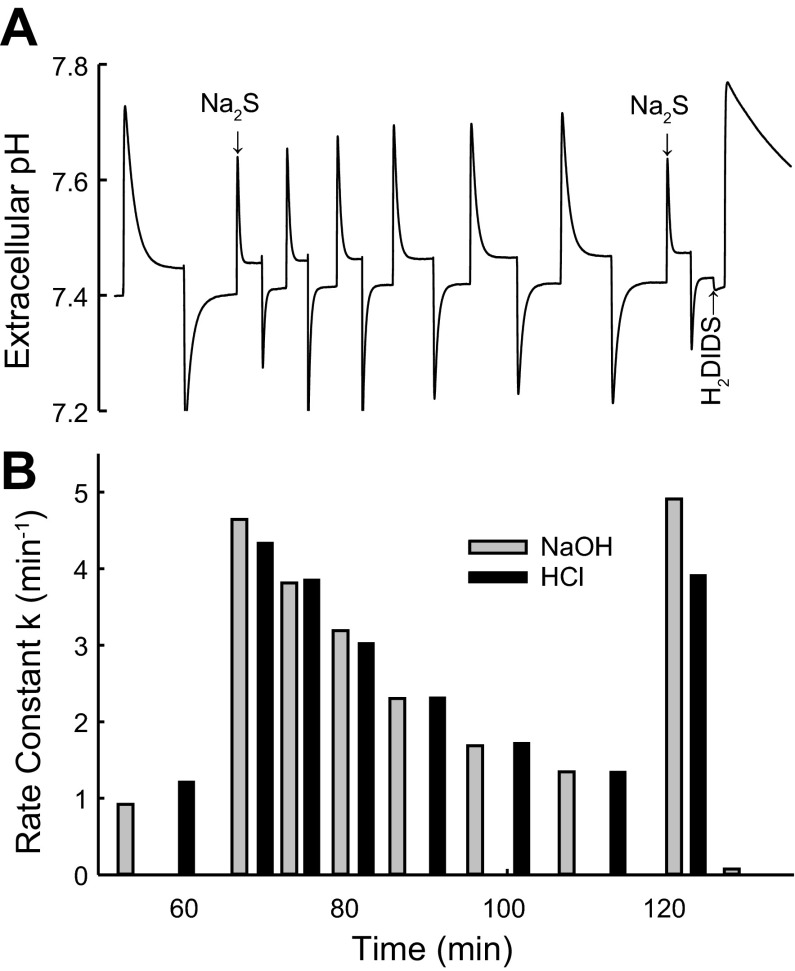
Stimulation of pH equilibration by addition of Na2S. Continuation of the experiment in Fig. 2. A: pH vs. time, with the last acid and base pulse in Fig. 2 repeated. Two upstrokes labeled Na2S represent addition of 5 μmol of Na2S from a 0.1 M stock solution that had been frozen until use. Other upstrokes and downstrokes represent additions of 5 μmol of NaOH and HCl, respectively. H2DIDS was added from a 5 mM stock solution to a final concentration of 10 μM. B: rate constants for pH equilibration calculated from the pH transients as described in Fig. 2 legend. In 4 experiments performed at equilibrium pH 7.35–7.45, the mean Na2S-stimulated rate constant for pH equilibration was 4.5 min−1 (range 3.9–5.5), measured immediately after the Na2S pulse.

After the initial addition of Na2S, pulses of HCl and NaOH were given alternately, and _k_pH decreased progressively over the next 30 min toward the baseline rate that existed before addition of Na2S (Fig. 3). The decrease in _k_pH was a consequence of loss of H2S, rather than irreversible H2S toxicity or rundown of the system, because a second addition of Na2S was followed by the same rapid pH equilibration as the first addition (Fig. 3). Finally, the AE1 inhibitor H2DIDS was added; _k_pH after a subsequent NaOH pulse was extremely small, indicating that the H2S/HS−-dependent pH equilibration requires a functioning anion exchanger. Rapid H2S/HS−-dependent, H2DIDS-inhibited pH equilibration was confirmed in each of nine separate experiments.

H2S/HS− Cycling at High pH

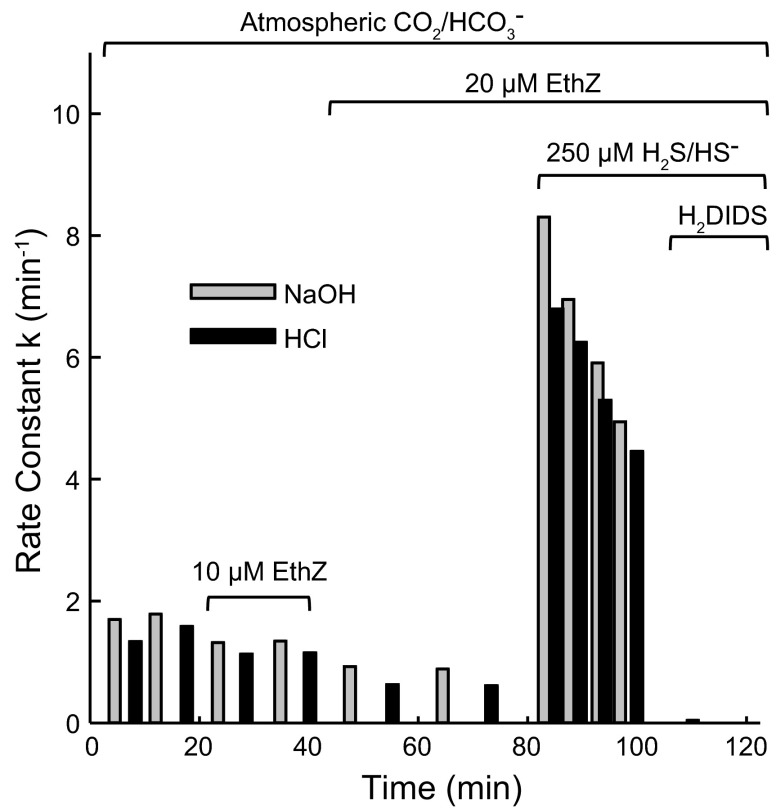
To determine whether the H2S transport limb of the cycle may be rate-limiting for acid/base transport by H2S/HS− cycling, experiments similar to that in Figs. 2 and 3 were conducted at equilibrium pHo 8.4, where the H2S concentration is much lower than the HS− concentration. As described previously, cells were suspended in weakly buffered 160 mM KCl as in Figs. 2 and 3, except NaOH and Na2CO3 were added to raise the equilibrium pHo. Once a stable pHo of 8.4 was reached, NaOH and HCl pulses were applied as in Figs. 2 and 3. The rate constants for decay of the pH transients are plotted in Fig. 4. The results are very similar to those at pH 7.4. Ethoxzolamide inhibits the CO2/HCO3− Jacobs-Stewart cycle, and the addition of Na2S causes a large increase in _k_pH. After Na2S addition, the pH equilibration rate declines somewhat more slowly than at pH 7.4, but the rate of decline is still substantial. The H2S/HS−-dependent acid/base fluxes at high pH are completely inhibited by H2DIDS, as was true at pH 7.4.

Fig. 4.

Fig. 4.

Rate constants for pH equilibration following NaOH or HCl pulses at equilibrium pH 8.4–8.45, 37°C, and atmospheric CO2 and with 160 mM KCl buffered with 1 mM glycylglycine and 0.5 mM HEPES. The first gray bar following the bracket labeled 250 μM H2S/HS− is the rate constant following a pulse of 5 μmol of Na2S rather than NaOH.

H2S evaporation will take place in any HS−-containing solution that is near neutral pH and open to the atmosphere (11), and an attempt was made to minimize the rate of H2S loss by sealing the tube around the pH electrode and minimizing head space. This raised the half time for loss of H2S (as measured by the decline in _k_pH at equilibrium pH ∼7.4) from ∼13 min in an open tube to ∼25–30 min in a sealed tube. A detailed investigation of the rate of H2S loss was not conducted, but at least part of the decline in _k_pH is clearly the result of H2S evaporation (see discussion).

Lack of Acceleration of pH Equilibration by SO2/HSO3−, HF/F−, or H3BO3/H4BO4−

Experiments similar to those with H2S/HS− were performed to determine whether other inorganic weak acid/anion pairs can transport acid by a Jacobs-Stewart cycle. In aqueous solution, SO2 hydration results in the production of HSO3− and H+: SO2 + H2O ↔ HSO3− + H+. The forward hydration reaction is rapid in the absence of catalyst (12), with a rate constant of 3.4 × 106 s−1; the reverse rate constant is 200 × 108 M−1·s−1. The permeability of the red cell membrane to HSO3− is higher than it is to SO42− but still much lower than to Cl− (38); the permeability to SO2 is not known but should be reasonably high. Despite the known rapid interconversion of SO2 and HSO3− and the fact that both are membrane-permeant, addition of Na2SO3 had no detectable effect on red cell pH equilibration; the same concentration of Na2S caused a major increase (Fig. 5). As described previously, the medium contained 160 mM NaCl.

Fig. 5.

Fig. 5.

Lack of stimulation of pH equilibration by Na2SO3. Cells were suspended in weakly buffered 160 mM KCl as described previously, and 20 μM ethoxzolamide was added to inhibit CO2-dependent pH equilibration. The number adjacent to each pH transient is the rate constant (min−1) for relaxation of the transient. Each arrow represents addition of 5 μmol of the indicated acid, base, or salt. Na2SO3 does not cause as large a pH transient as Na2S, because SO32− is not as strong a base as S2−. Rate constant for relaxation of the transient could nonetheless be measured and is not detectably different from the rate constant following NaOH. As described previously, Na2S stimulates the rate of pH equilibration by ∼5 min−1, with the rate decaying with subsequent acid and base additions.

F− was also examined to determine whether it can act with HF in a Jacobs-Stewart cycle. HF is a weak acid (p_K_ = 3.2) compared with other mineral acids, and there will be a small amount of HF in solution at pH 7.4. Addition of 250 μM NaF to the NaCl medium had no detectable effect on the rate of pH equilibration at pH 7.4 in the presence of 20 μM ethoxzolamide.

AE1 homologs in Arabidopsis (63) and Saccharomyces cerevisiae (32, 62) can transport boric acid. The human SLC4 member BTR1 (52) is believed to be a borate transporter (51). It is therefore possible that AE1 transports H4BO4− and that boric acid/borate can act in a Jacobs-Stewart cycle. However, as was true of HSO3− and F−, addition of 250 μM H3BO3 had no effect on _k_pH equilibration. The experiment was conducted at pH 8 to increase the concentration of H4BO4− (p_K_a 9.3).

DISCUSSION

HS− Is a Very Good Substrate for AE1

The data presented here represent the first published estimates of the rates of H2S and HS− transport across a mammalian cell membrane. The results show that H2S and HS− can act in a Jacobs-Stewart cycle to transport acid equivalents across the human erythrocyte membrane. This finding indicates that not only is H2S highly permeant, but HS− is a very good substrate for the anion exchanger AE1. The half times for HS− and H2S transport are <1 s (see below). It was possible to estimate these rapid rates from the slower rates of pH equilibration (half time ∼9 s), because HS− and H2S recycle many times as the cells and medium approach a new Donnan equilibrium after an acid or base pulse; accordingly, the half time for pH equilibration is much longer than the individual half times for transport of HS− and H2S.

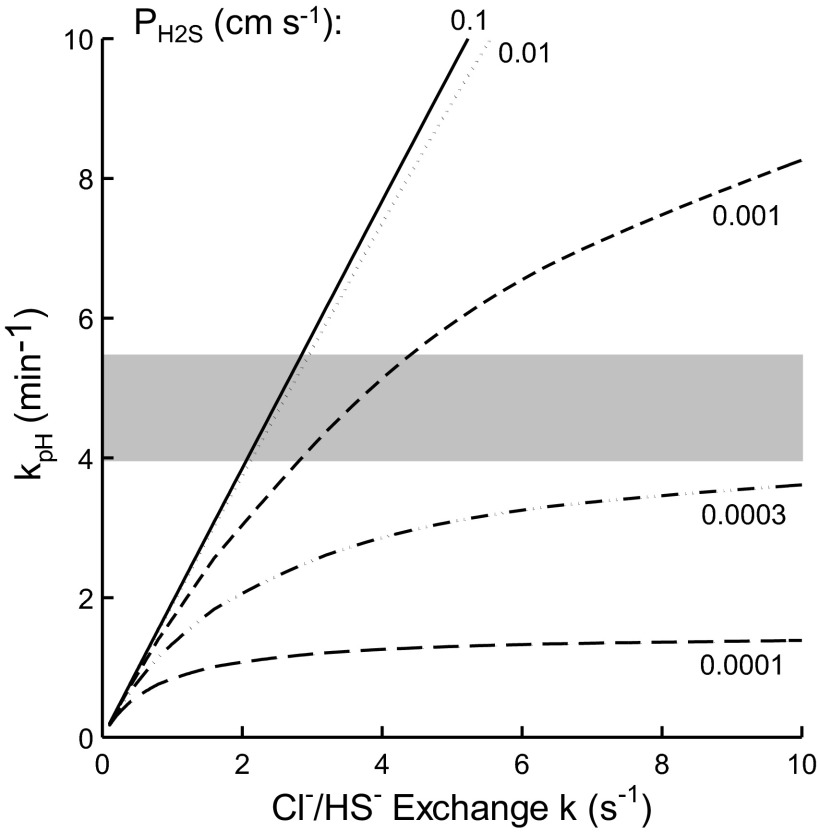
The values of _k_pH predicted from the Jacobs-Stewart cycle for these conditions (see Modeling) are plotted in Fig. 6 as a function of the unimolecular rate constant _k_ex (s−1) for Cl−/HS− exchange for various values of _P_H2S. The model predicts that if _P_H2S is larger than ∼0.01 cm/s, the cycle is limited mainly by Cl−/HS− exchange, and the _k_pH of 4.5 min−1 (range 3.9–5.5 in 4 experiments at pH 7.4) corresponds to a Cl−/HS− exchange rate constant _k_ex of ∼2.5 s−1. This rate is ∼30% of the rate constant for Cl−/HCO3− exchange at this pH and temperature (5, 72). If _P_H2S = 10−3 cm/s, the Cl−/HCO3− exchange rate would need to be slightly higher (∼3.5 s−1) to account for the observed _k_pH (Fig. 6).

Fig. 6.

Fig. 6.

Rate constant (min−1) for sulfide-dependent pH equilibration predicted by the Jacobs-Stewart cycle plotted vs. rate constant _k_ex (s−1) for Cl−/HS− exchange for various values of the H2S permeability coefficient _P_H2S (cm/s). Predicted value of _k_pH was calculated as described in Modeling, with extracellular buffer power one-eighth of intracellular buffer power. Gray zone represents range of values of sulfide-dependent _k_pH at equilibrium pH 7.3–7.5 for the same buffer conditions (_k_pH = 3.9–5.5 min−1, 4 experiments). If _P_H2S is >0.001 cm/s, the observed rate is mainly limited by Cl−/HS− exchange and requires a Cl−/HS− exchange rate constant ≥2.5 s−1. If _P_H2S is <0.0003 cm/s, even a very high Cl−/HS− exchange rate could not explain the _k_pH at pH 7.4, because the cycle would be limited by H2S transport.

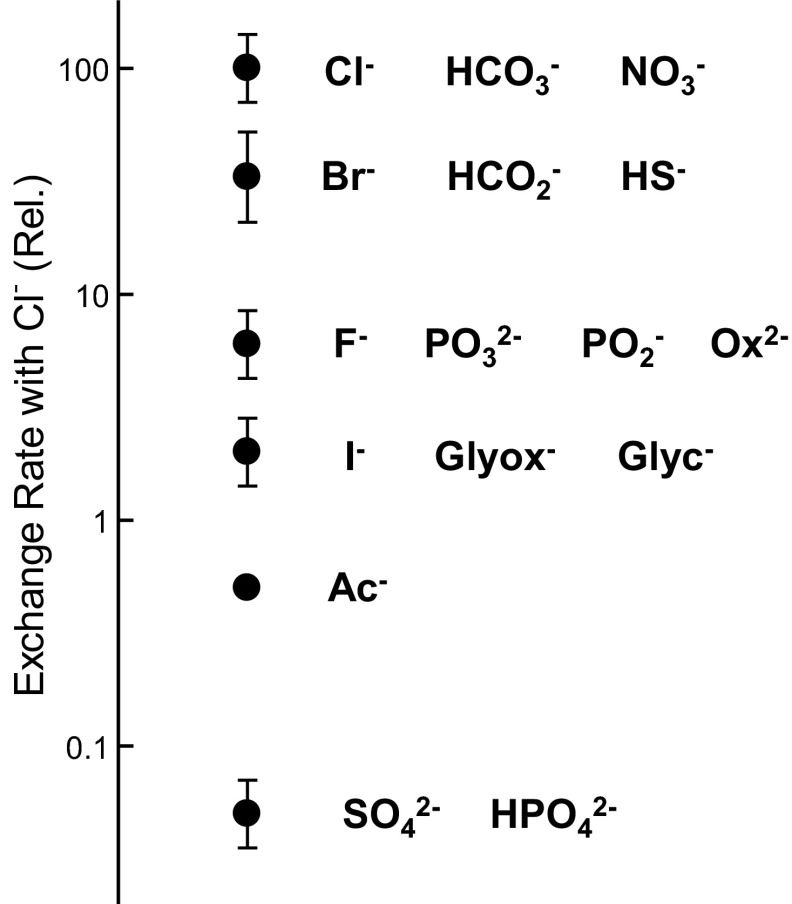
To provide a context for the Cl−/HS− exchange rate inferred from the _k_pH data, the relative rates of exchange of Cl− for various anions in human erythrocytes are summarized in Fig. 7. The comparisons are only semiquantitative, because the measurements were done at different temperatures, but the rank order of the anions should be reasonably accurate. The only anions that are transported more rapidly than HS− in exchange for Cl− are Cl− itself, HCO3−, and NO3−. The rates of Cl−/Br−, Cl−/HCO2−, and Cl−/HS− exchange are all roughly one-third of those of the fastest anions. Many other known AE1 substrates exchange for Cl− more slowly and, in most cases, orders of magnitude more slowly, as summarized in Fig. 7.

Fig. 7.

Fig. 7.

Relative Cl−/X− exchange rates for various inorganic and organic anions via mammalian AE1. Present data indicate that the Cl−/HS− exchange rate is about one-third that of Cl− and HCO3− and is comparable to that of Cl−/Br− exchange (19, 20, 64) and Cl−/formate exchange (23, 30). F−, I− (64), oxalate (Ox2−), glycolate (Glyc−), glyoxalate (Glyox−) (30), phosphate, phosphite, hypophosphite (16), acetate (Ac−) (18, 20), and sulfate (47) exchange for Cl− much more slowly.

Estimate of the Lower Limit of PH2S

The pH equilibration experiments also place a lower limit on _P_H2S. As indicated above, the experiments at pH 7.4 imply that _P_H2S is >10−3 cm/s (Fig. 6). Experiments at higher pH place a further restriction on _P_H2S, because H2S represents a smaller fraction of total S at higher pH. In two experiments at equilibrium pH 8.4, including that in Fig. 4, the sulfide-dependent _k_pH was ∼6.6 min−1 (the same extracellular buffer power noted previously). To account for this _k_pH, _P_H2S must be ≥0.01 cm/s and could very easily be in the range estimated for lipid bilayers, i.e., >0.5 cm/s (46). With a cell water volume-to-surface area ratio of 0.45 × 10−4 cm, _P_H2S of 0.01 cm/s corresponds to a unimolecular rate constant of 222 s−1, or a half time of 0.003 s. Equilibration of H2S across the erythrocyte membrane therefore takes place over times that are very short compared with capillary transit times.

Half-Life of H2S/HS− in a Suspension of Human Erythrocytes

In our experiments, after addition of 250 μM Na2S, _k_pH increased immediately but then decayed with a half time of 10–15 min in a tube exposed to the atmosphere (Fig. 3). The suspensions were stirred but not bubbled with gas, and the rate of H2S loss was consistent with the evaporative H2S loss rates in stirred solutions measured by DeLeon et al. (11); strict comparison of rates is impossible, because the surface area-to-volume ratios in the vessels were likely different in the two studies.

In a capped tube, the decay of the rate of pH equilibration after Na2S addition is slower than in an open tube (half time ∼25 min; data not shown). There could have been some leakage of H2S from the capped tube, but it is also very likely that some of the H2S loss is by mechanisms other than evaporation. Whitfield et al. (71) showed that, following addition of 10 μM Na2S to whole blood of several different mammals, the total sulfide concentration decays more rapidly (half time 1–2 min) than in the present experiments. This rapid disappearance of H2S/HS− cannot be explained by evaporation. Therefore, erythrocytes and plasma consume H2S. The reason for the slower rates of H2S loss in the present study than in the study of Whitfield et al. could be that an 8% suspension of washed cells, instead of whole blood, was used here, and the initial concentration of Na2S was 25-fold higher in the present experiments.

At an 8% hematocrit, there is a molar excess of hemoglobin relative to 250 μM S. Although many nonmammalian hemoglobins bind sulfide (49) and mammalian hemoglobins can form sulfhemoglobin under some conditions, mammalian oxyhemoglobin in the presence of H2S does not form sulfhemoglobin (4). Instead, some other process results in the consumption of H2S by erythrocytes; the mechanism of H2S loss is not known. It is worth pointing out that H2S consumption by blood, although it takes place at a very appreciable rate (71), is still slow compared with the transport of H2S and HS− in erythrocytes, each of which has a half time of well under 1 s. H2S and HS− can therefore enter and exit the erythrocyte many times before they are converted to some other compound.

Implications Regarding the Disposition of Tissue-Produced H2S

The high H2S permeability of the erythrocyte membrane inferred from the present experiments is consistent with the finding that lipid bilayers, even those with high cholesterol, have a very high H2S permeability (46). Pathways for H2S transport in human erythrocytes may include aquaporin and/or other channels in addition to diffusion through the bilayer; the present work does not distinguish among different pathways for H2S transport. The high erythrocyte H2S permeability implies that tissue-produced H2S will equilibrate with erythrocyte cytosol very quickly in the microcirculation. The next generation of diffusional models for the disposition of tissue-produced H2S (7) will need to take into account the rapid erythrocyte transport of H2S and HS−, which will result in a reduction of the concentration of H2S in the extracellular fluid surrounding H2S-producing cells.

Physiologically, the H2S/HS− cycling observed here should not be sufficient to change red cell acid-base status, because the blood concentrations of H2S/HS− are undoubtedly much lower than those used here (71). Also, in whole blood the HCO3− concentration is 100-fold higher than in the present experiments, and CO2/HCO3− will dominate acid/base fluxes across the erythrocyte membrane.

Does net H+ transport by cycling of endogenous H2S/HS− have a physiological or pathophysiological role in any cell? Perhaps it does, but the requirements are relatively stringent. The membrane must have a relatively high rate of HS−/Cl− exchange as well as high H2S permeability, and there must be sufficient H2S and HS− to generate significant mass flow through the cycle to drive pH toward Donnan equilibrium with Cl−. It is not known whether these requirements are met in any mammalian cell, but certainly in most cells, Jacobs-Stewart H2S/HS− cycling is very unlikely to affect pHi under physiological conditions.

Implications Regarding Experiments Involving Additions of Na2S or NaHS to Biological Systems

The experiments described here strictly apply only to AE1, which is expressed at high levels mainly in erythrocytes and the α intercalated cells of the kidney collecting duct (2, 59). However, given the sequence similarities in the membrane domains of AE1 and the Cl−/HCO3− exchangers AE2 and AE3 (2), it is likely that HS− is a reasonably good substrate for these transporters as well. HS− could also be a substrate for other Cl− transporters such as members of SLC26 (3, 60) and possibly the Cl−-coupled cation cotransporters of the SLC12 family (22, 55). Therefore, in any experiment with exogenously applied H2S/HS−, it is possible that the observed effects are at least in part a consequence of HS− acting as a substrate for an anion transporter.

For example, 0.01–1 mM NaHS causes a DIDS-sensitive decrease in pHi and also increases the rate of apparent Cl−/HCO3− exchange in A7r5 vascular smooth muscle cells (39). These effects could, in principle, be the result of Cl−/HS− exchange and H2S transport in a Jacobs-Stewart cycle as described above, rather than a regulatory effect of H2S on a transporter. There are other examples of DIDS blocking effects of H2S/HS− (35, 42, 70); these effects could be partially related to the role of HS− as a substrate for an anion exchanger. The erythrocyte has a far higher capacity for Cl− exchange than most other cells, but any cell with an anion exchanger that can transport HS− will in principle carry out an acid-transporting cycle in the presence of H2S/HS−.

Comparison of the Jacobs-Stewart Cycle for CO2/HCO3−, H2S/HS−, and Other Weak Inorganic Acids

The finding that the Jacobs-Stewart cycle is more efficient with H2S/HS− than CO2/HCO3− may seem surprising initially but can be explained very easily by the fact that H2S-HS− interconversion is very fast in both cells and medium, whereas extracellular CO2/HCO3− hydration/dehydration is normally relatively slow, as pointed out in the original work of Jacobs and Stewart (27). Steady-state modeling of the Jacobs-Stewart cycle for CO2/HCO3−, using parameters from the literature for all the rate processes (see Modeling), results in a predicted CO2-dependent _k_pH of ∼1.6 min−1 at pH 7.4 with atmospheric CO2 and the extracellular buffer power used in these experiments. This is remarkably close to the ethoxzolamide-inhibitable rate observed in Fig. 2; therefore, with no adjustable parameters, the model predicts the CO2/HCO3−-dependent pH equilibration rate very well.

It is noteworthy that, at pHo 8.4, the H2S/HS−-stimulated _k_pH is much higher than the ethoxzolamide-sensitive rate (Fig. 4), despite the fact that, at this pH (and atmospheric CO2), the HCO3− concentration is much higher than the HS− concentration. The reason for this is that even though the H2S concentration is relatively low at pH 8.4, the rate of H2S transport and H2S/HS− interconversion are both very rapid, and the cycle is limited by Cl−/HS− exchange. The cycle for CO2/HCO3−, in contrast, is limited largely by extracellular hydration/dehydration.

It is difficult to identify an anion exchange partner for Cl− that is better suited for the Jacobs-Stewart cycle than HS−. The anion exchange rate, acid permeation rate, and the protonation-deprotonation reactions are rapid, and, importantly, the p_K_a is neutral. By comparison, the other inorganic anions tested (F−, HSO3−, and H4BO4−) do not detectably accelerate pH equilibration when tested at the same concentration as H2S/S−. For F−, the exchange rate with Cl− is reasonably fast (64), but the p_K_a for HF is 3.17, and the cycle is limited by the low concentration of free HF at neutral pH. The same is true of SO2/HSO3− (effective p_K_a 1.8). For H3BO3/H4BO4−, the experiments were conducted at a pH reasonably close to the p_K_a, but there was still no acceleration of pH equilibration. It is not clear whether the anion exchange or the free acid permeation limb of the cycle is slow, but one or both must be.

CO2- and H2S-Independent pH Equilibration

In the presence of 20 μM ethoxzolamide (and before addition of Na2S), the rate constant for pH equilibration at pH ∼7.4 is slightly higher after HCl addition than after NaOH addition (Fig. 2 and 2 additional experiments). This finding is consistent with the idea that, as proposed previously (29), the main pathway for CO2-independent pH equilibration is AE1-mediated H+-Cl− cotransport, rather than Cl−/OH− exchange. The reasoning is as follows. After the HCl pulse, the rate of equilibration was measured over a lower pHo range than after the NaOH pulse, and the absolute value of the driving force for H+-Cl− cotransport ([H+]o[Cl−]o − [H+]i[Cl−]i) is larger after the HCl pulse than after the NaOH pulse. Interestingly, at pH 8.4, the rate constant is slightly higher after NaOH addition than after HCl addition (Fig. 4 and 1 additional experiment). This finding is consistent with the idea that CO2-independent pH equilibration results from AE1-mediated Cl−/OH− exchange at high pH; this range of pH was not examined in our previous work (29).

Summary

In summary, HS−, which is the predominant form of H2S at physiological pH, is a remarkably good substrate for the erythrocyte anion exchange protein AE1. HS− exchange with Cl− is as rapid as that of any Cl− exchange partner other than Cl− itself, HCO3−, and NO3−. The acid-base pair H2S/HS− can carry out acid transport by the Jacobs-Stewart cycle more efficiently than CO2/HCO3−, because the H2S p_K_a is close to 7 and the protonation reactions for sulfide do not require a hydration step. The rapid transport of H2S and HS− implies that erythrocytes should be a very efficient sink for endogenous H2S in the microcirculation. In any experiment in which exogenous Na2S or NaHS is added to cells that have an inorganic anion exchange protein, the effect of HS− could in principle be a consequence of the fact that Cl−/HS− exchange, in combination with rapid H2S diffusion, can carry out net acid transport by the Jacobs-Stewart cycle.

GRANTS

This work was supported in part by National Institute of General Medical Sciences Grant R01 GM-026861.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author.

AUTHOR CONTRIBUTIONS

M.L.J. is responsible for conception and design of the research; M.L.J. performed the experiments; M.L.J. analyzed the data; M.L.J. interpreted the results of the experiments; M.L.J. prepared the figures; M.L.J. drafted the manuscript; M.L.J. edited and revised the manuscript; M.L.J. approved the final version of the manuscript.

ACKNOWLEDGMENTS

The author is grateful to K. David Straub for helpful discussions. The author thanks Judy Dent and Jerry Ware for providing the human red blood cells.

REFERENCES