Definitions, methods, and applications in interpretable machine learning (original) (raw)

Significance

The recent surge in interpretability research has led to confusion on numerous fronts. In particular, it is unclear what it means to be interpretable and how to select, evaluate, or even discuss methods for producing interpretations of machine-learning models. We aim to clarify these concerns by defining interpretable machine learning and constructing a unifying framework for existing methods which highlights the underappreciated role played by human audiences. Within this framework, methods are organized into 2 classes: model based and post hoc. To provide guidance in selecting and evaluating interpretation methods, we introduce 3 desiderata: predictive accuracy, descriptive accuracy, and relevancy. Using our framework, we review existing work, grounded in real-world studies which exemplify our desiderata, and suggest directions for future work.

Keywords: interpretability, machine learning, explainability, relevancy

Abstract

Machine-learning models have demonstrated great success in learning complex patterns that enable them to make predictions about unobserved data. In addition to using models for prediction, the ability to interpret what a model has learned is receiving an increasing amount of attention. However, this increased focus has led to considerable confusion about the notion of interpretability. In particular, it is unclear how the wide array of proposed interpretation methods are related and what common concepts can be used to evaluate them. We aim to address these concerns by defining interpretability in the context of machine learning and introducing the predictive, descriptive, relevant (PDR) framework for discussing interpretations. The PDR framework provides 3 overarching desiderata for evaluation: predictive accuracy, descriptive accuracy, and relevancy, with relevancy judged relative to a human audience. Moreover, to help manage the deluge of interpretation methods, we introduce a categorization of existing techniques into model-based and post hoc categories, with subgroups including sparsity, modularity, and simulatability. To demonstrate how practitioners can use the PDR framework to evaluate and understand interpretations, we provide numerous real-world examples. These examples highlight the often underappreciated role played by human audiences in discussions of interpretability. Finally, based on our framework, we discuss limitations of existing methods and directions for future work. We hope that this work will provide a common vocabulary that will make it easier for both practitioners and researchers to discuss and choose from the full range of interpretation methods.

Machine learning (ML) has recently received considerable attention for its ability to accurately predict a wide variety of complex phenomena. However, there is a growing realization that, in addition to predictions, ML models are capable of producing knowledge about domain relationships contained in data, often referred to as interpretations. These interpretations have found uses in their own right, e.g., medicine (1), policymaking (2), and science (3, 4), as well as in auditing the predictions themselves in response to issues such as regulatory pressure (5) and fairness (6). In these domains, interpretations have been shown to help with evaluating a learned model, providing information to repair a model (if needed), and building trust with domain experts (7).

In the absence of a well-formed definition of interpretability, a broad range of methods with a correspondingly broad range of outputs (e.g., visualizations, natural language, mathematical equations) have been labeled as interpretation. This has led to considerable confusion about the notion of interpretability. In particular, it is unclear what it means to interpret something, what common threads exist among disparate methods, and how to select an interpretation method for a particular problem/audience.

In this paper, we attempt to address these concerns. To do so, we first define interpretability in the context of machine learning and place it within a generic data science life cycle. This allows us to distinguish between 2 main classes of interpretation methods: model based* and post hoc. We then introduce the predictive, descriptive, relevant (PDR) framework, consisting of 3 desiderata for evaluating and constructing interpretations: predictive accuracy, descriptive accuracy, and relevancy, where relevancy is judged by a human audience. Using these terms, we categorize a broad range of existing methods, all grounded in real-world examples.† In doing so, we provide a common vocabulary for researchers and practitioners to use in evaluating and selecting interpretation methods. We then show how our work enables a clearer discussion of open problems for future research.

1. Defining Interpretable Machine Learning

On its own, interpretability is a broad, poorly defined concept. Taken to its full generality, to interpret data means to extract information (of some form) from them. The set of methods falling under this umbrella spans everything from designing an initial experiment to visualizing final results. In this overly general form, interpretability is not substantially different from the established concepts of data science and applied statistics.

Instead of general interpretability, we focus on the use of interpretations to produce insight from ML models as part of the larger data–science life cycle. We define interpretable machine learning as the extraction of relevant knowledge from a machine-learning model concerning relationships either contained in data or learned by the model. Here, we view knowledge as being relevant if it provides insight for a particular audience into a chosen problem. These insights are often used to guide communication, actions, and discovery. They can be produced in formats such as visualizations, natural language, or mathematical equations, depending on the context and audience. For instance, a doctor who must diagnose a single patient will want qualitatively different information than an engineer determining whether an image classifier is discriminating by race. What we define as interpretable ML is sometimes referred to as explainable ML, intelligible ML, or transparent ML. We include these headings under our definition.

2. Background

Interpretability is a quickly growing field in machine learning, and there have been multiple works examining various aspects of interpretations (sometimes under the heading, explainable AI). One line of work focuses on providing an overview of different interpretation methods with a strong emphasis on post hoc interpretations of deep learning models (8, 9), sometimes pointing out similarities between various methods (10, 11). Other work has focused on the narrower problem of evaluating interpretations (12, 13) and what properties they should satisfy (14). These previous works touch on different subsets of interpretability, but do not address interpretable machine learning as a whole, and give limited guidance on how interpretability can actually be used in data–science life cycles. We aim to do so by providing a framework and vocabulary to fully capture interpretable machine learning, its benefits, and its applications to concrete data problems.

Interpretability also plays a role in other research areas. For example, interpretability is a major topic when considering bias and fairness in ML models (15–17). In psychology, the general notions of interpretability and explanations have been studied at a more abstract level (18, 19), providing relevant conceptual perspectives. Additionally, we comment on 2 related areas that are distinct but closely related to interpretability: causal inference and stability.

Causal Inference.

Causal inference (20) is a subject from statistics which is related, but distinct, from interpretable machine learning. According to a prevalent view, causal inference methods focus solely on extracting causal relationships from data, i.e., statements that altering one variable will cause a change in another. In contrast, interpretable ML, and most other statistical techniques, is used to describe general relationships. Whether or not these relationships are causal cannot be verified through interpretable ML techniques, as they are not designed to distinguish between causal and noncausal effects.

In some instances, researchers use both interpretable machine learning and causal inference in a single analysis (21). One form of this is where the noncausal relationships extracted by interpretable ML are used to suggest potential causal relationships. These relationships can then be further analyzed using causal inference methods and fully validated through experimental studies.

Stability.

Stability, as a generalization of robustness in statistics, is a concept that applies throughout the entire data–science life cycle, including interpretable ML. The stability principle requires that each step in the life cycle is stable with respect to appropriate perturbations, such as small changes in the model or data. Recently, stability has been shown to be important in applied statistical problems, for example when trying to make conclusions about a scientific problem (22) and in more general settings (23). Stability can be helpful in evaluating interpretation methods and is a prerequisite for trustworthy interpretations. That is, one should not interpret parts of a model which are not stable to appropriate perturbations to the model and data. This is demonstrated through examples in the text (21, 24, 25).

3. Interpretation in the Data–Science Life Cycle

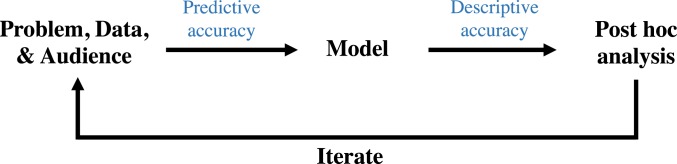
Before discussing interpretation methods, we first place the process of interpretable ML within the broader data–science life cycle. Fig. 1 presents a deliberately general description of this process, intended to capture most data-science problems. What is generally referred to as interpretation largely occurs in the modeling and post hoc analysis stages, with the problem, data, and audience providing the context required to choose appropriate methods.

Fig. 1.

Fig. 1.

Overview of different stages (black text) in a data–science life cycle where interpretability is important. Main stages are discussed in Section 3 and accuracy (blue text) is described in Section 4.

Problem, Data, and Audience.

At the beginning of the cycle, a data–science practitioner defines a domain problem that the practitioner wishes to understand using data. This problem can take many forms. In a scientific setting, the practitioner may be interested in relationships contained in the data, such as how brain cells in a particular area of the visual system relate to visual stimuli (26). In industrial settings, the problem often concerns the predictive performance or other qualities of a model, such as how to assign credit scores with high accuracy (27) or do so fairly with respect to gender and race (17). The nature of the problem plays a role in interpretability, as the relevant context and audience are essential in determining what methods to use.

After choosing a domain problem, the practitioner collects data to study it. Aspects of the data-collection process can affect the interpretation pipeline. Notably, biases in the data (i.e., mismatches between the collected data and the population of interest) will manifest themselves in the model, restricting one’s ability to generalize interpretations generated from the data to the population of interest.

Model.

Based on the chosen problem and collected data, the practitioner then constructs a predictive model. At this stage, the practitioner processes, cleans, and visualizes data; extracts features; selects a model (or several models); and fits it. Interpretability considerations often come into play in this step related to the choice between simpler, easier to interpret models and more complex, black-box models, which may fit the data better. The model’s ability to fit the data is measured through predictive accuracy.

Post Hoc Analysis.

Having fitted a model (or models), the practitioner then analyzes it for answers to the original question. The process of analyzing the model often involves using interpretability methods to extract various (stable) forms of information from the model. The extracted information can then be analyzed and displayed using standard data analysis methods, such as scatter plots and histograms. The ability of the interpretations to properly describe what the model has learned is denoted by descriptive accuracy.

Iterate.

If sufficient answers are uncovered after the post hoc analysis stage, the practitioner finishes. Otherwise, the practitioner updates something in the chain (problem, data, and/or model) and the iterate (28). Note that the practitioner can terminate the loop at any stage, depending on the context of the problem.

Interpretation Methods within the PDR Framework.

In the framework described above, our definition of interpretable ML focuses on methods in either the modeling or post hoc analysis stages. We call interpretability in the modeling stage model-based interpretability (Section 5). This part of interpretability is focused upon the construction of models that readily provide insight into the relationships they have learned. To provide this insight, model-based interpretability techniques must generally use simpler models, which can result in lower predictive accuracy. Consequently, model-based interpretability is best used when the underlying relationship is sufficiently simple that model-based techniques can achieve reasonable predictive accuracy or when predictive accuracy is not a concern.

We call interpretability in the post hoc analysis stage post hoc interpretability (Section 6). In contrast to model-based interpretability, which alters the model to allow for interpretation, post hoc interpretation methods take a trained model as input and extract information about what relationships the model has learned. They are most helpful when the data are especially complex, and practitioners need to train a black-box model to achieve reasonable predictive accuracy.

After discussing desiderata for interpretation methods, we investigate these 2 forms of interpretations in detail and discuss associated methods.

4. The PDR Desiderata for Interpretations

In general, it is unclear how to select and evaluate interpretation methods for a particular problem and audience. To help guide this process, we introduce the PDR framework, consisting of 3 desiderata that should be used to select interpretation methods for a particular problem: predictive accuracy, descriptive accuracy, and relevancy.

A. Accuracy.

The information produced by an interpretation method should be faithful to the underlying process the practitioner is trying to understand. In the context of ML, there are 2 areas where errors can arise: when approximating the underlying data relationships with a model (predictive accuracy) and when approximating what the model has learned using an interpretation method (descriptive accuracy). For an interpretation to be trustworthy, one should try to maximize both of the accuracies. In cases where either accuracy is not very high, the resulting interpretations may still be useful. However, it is especially important to check their trustworthiness through external validation, such as running an additional experiment.

A.1. Predictive accuracy.

The first source of error occurs during the model stage, when an ML model is constructed. If the model learns a poor approximation of the underlying relationships in the data, any information extracted from the model is unlikely to be accurate. Evaluating the quality of a model’s fit has been well studied in standard supervised ML frameworks, through measures such as test-set accuracy. In the context of interpretation, we describe this error as predictive accuracy.

Note that in problems involving interpretability, one must appropriately measure predictive accuracy. In particular, the data used to check for predictive accuracy must resemble the population of interest. For instance, evaluating on patients from one hospital may not generalize to others. Moreover, problems often require a notion of predictive accuracy that goes beyond just average accuracy. The distribution of predictions matters. For instance, it could be problematic if the prediction error is much higher for a particular class. Finally, the predictive accuracy should be stable with respect to reasonable data and model perturbations. One should not trust interpretations from a model which changes dramatically when trained on a slightly smaller subset of the data.

A.2. Descriptive accuracy.

The second source of error occurs during the post hoc analysis stage, when interpretation methods are used to analyze a fitted model. Oftentimes, interpretations provide an imperfect representation of the relationships learned by a model. This is especially challenging for complex black-box models such as neural networks, which store nonlinear relationships between variables in nonobvious forms.

Definition:

We define descriptive accuracy, in the context of interpretation, as the degree to which an interpretation method objectively captures the relationships learned by machine-learning models.

A.3. A common conflict: predictive vs. descriptive accuracy.

In selecting what model to use, practitioners are sometimes faced with a trade-off between predictive and descriptive accuracy. On the one hand, the simplicity of model-based interpretation methods yields consistently high descriptive accuracy, but can sometimes result in lower predictive accuracy on complex datasets. On the other hand, in complex settings such as image analysis, complicated models can provide high predictive accuracy, but are harder to analyze, resulting in a lower descriptive accuracy.

B. Relevancy.

When selecting an interpretation method, it is not enough for the method to have high accuracy—the extracted information must also be relevant. For example, in the context of genomics, a patient, doctor, biologist, and statistician may each want different (yet consistent) interpretations from the same model. The context provided by the problem and data stages in Fig. 1 guides what kinds of relationships a practitioner is interested in learning about and by extension the methods that should be used.

Definition:

We define an interpretation to be relevant if it provides insight for a particular audience into a chosen domain problem.

Relevancy often plays a key role in determining the trade-off between predictive and descriptive accuracy. Depending on the context of the problem at hand, a practitioner may choose to focus on one over the other. For instance, when interpretability is used to audit a model’s predictions, such as to enforce fairness, descriptive accuracy can be more important. In contrast, interpretability can also be used solely as a tool to increase the predictive accuracy of a model, for instance, through improved feature engineering.

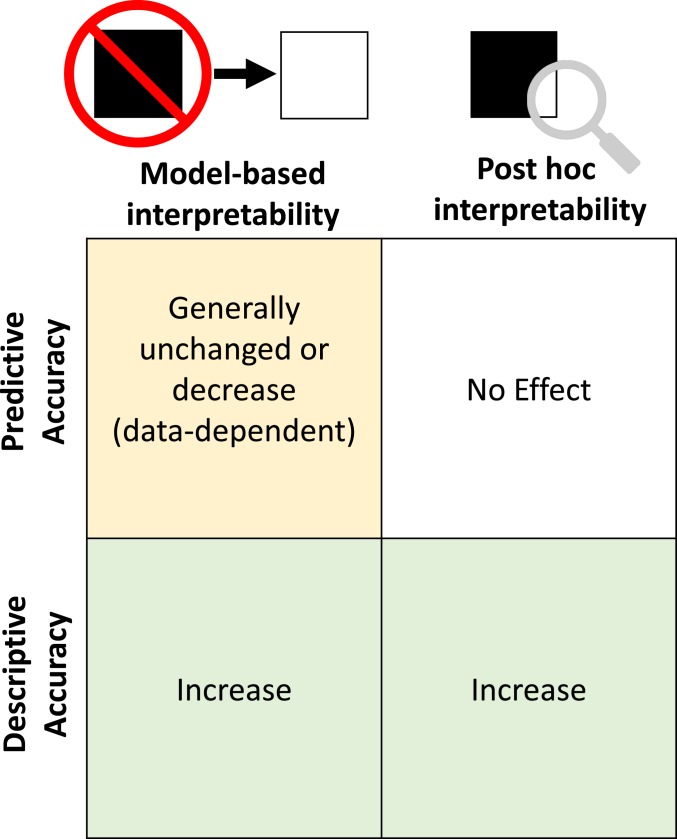
Having outlined the main desiderata for interpretation methods, we now discuss how they link to interpretation in the modeling and post hoc analysis stages in the data–science life cycle. Fig. 2 draws parallels between our desiderata for interpretation techniques introduced in Section 4 and our categorization of methods in Sections 5 and 6. In particular, both post hoc and model-based methods aim to increase descriptive accuracy, but only the model-based method affects the predictive accuracy. Not shown is relevancy, which determines what type of output is helpful for a particular problem and audience.

Fig. 2.

Fig. 2.

Impact of interpretability methods on descriptive and predictive accuracies. Model-based interpretability (Section 5) involves using a simpler model to fit the data which can negatively affect predictive accuracy, but yields higher descriptive accuracy. Post hoc interpretability (Section 6) involves using methods to extract information from a trained model (with no effect on predictive accuracy). These correspond to the model and post hoc stages in Fig. 1.

5. Model-Based Interpretability

We now discuss how interpretability considerations come into play in the modeling stage of the data–science life cycle (Fig. 1). At this stage, the practitioner constructs an ML model from the collected data. We define model-based interpretability as the construction of models that readily provide insight into the relationships they have learned. Different model-based interpretability methods provide different ways of increasing descriptive accuracy by constructing models which are easier to understand, sometimes resulting in lower predictive accuracy. The main challenge of model-based interpretability is to come up with models that are simple enough to be easily understood by the audience, while maintaining high predictive accuracy.

In selecting a model to solve a domain problem, the practitioner must consider the entirety of the PDR framework. The first desideratum to consider is predictive accuracy. If the constructed model does not accurately represent the underlying problem, any subsequent analysis will be suspect (29, 30). Second, the main purpose of model-based interpretation methods is to increase descriptive accuracy. Finally, the relevancy of a model’s output must be considered and is determined by the context of the problem, data, and audience. We now discuss some common types of model-based interpretability methods.

A. Sparsity.

When the practitioner believes that the underlying relationship in question is based upon a sparse set of signals, the practitioner can impose sparsity on the model by limiting the number of nonzero parameters. In this section, we focus on linear models, but sparsity can be helpful more generally. When the number of nonzero parameters is sufficiently small, a practitioner can interpret the variables corresponding to those parameters as being meaningfully related to the outcome in question and can also interpret the magnitude and direction of the parameters. However, before one can interpret a sparse parameter set, one should check for stability of the parameters. For example, if the signs/magnitudes of parameters or the predictions change due to small perturbations in the dataset, the coefficients should not be interpreted (31).

When the practitioner is able to correctly incorporate sparsity into the model, it can improve all 3 interpretation desiderata. By reducing the number of parameters to analyze, sparse models can be easier to understand, yielding higher descriptive accuracy. Moreover, incorporating prior information in the form of sparsity into a sparse problem can help a model achieve higher predictive accuracy and yield more relevant insights. Note that incorporating sparsity can often be quite difficult, as it requires understanding the data-specific structure of the sparsity and how it can be modeled.

Methods for obtaining sparsity often utilize a penalty on a loss function, such as LASSO (32) and sparse coding (33), or on model selection criteria such as AIC or BIC (34, 35). Many search-based methods have been developed to find sparse solutions. These methods search through the space of nonzero coefficients using classical subset-selection methods [e.g., orthogonal matching pursuit (36)]. Model sparsity is often useful for high-dimensional problems, where the goal is to identify key features for further analysis. For instance, sparsity penalties have been incorporated into random forests to identify a sparse subset of important features (37).

In the following example from genomics, sparsity is used to increase the relevancy of an interpretation by reducing the number of potential interactions to a manageable level.

Example (Ex):

Identifying interactions among regulatory factors or biomolecules is an important question in genomics. Typical genomic datasets include thousands or even millions of features, many of which are active in specific cellular or developmental contexts. The massive scale of such datasets makes interpretation a considerable challenge. Sparsity penalties are frequently used to make the data manageable for statisticians and their collaborating biologists to discuss and identify promising candidates for further experiments.

For instance, one recent study (24) uses a biclustering approach based on sparse canonical correlation analysis (SCCA) to identify interactions among genomic expression features in Drosophila melanogaster (fruit flies) and Caenorhabditis elegans (roundworms). Sparsity penalties enable key interactions among features to be summarized in heatmaps which contain few enough variables for a human to analyze. The authors of this study also perform stability analysis, finding their model to be robust to different initializations and perturbations to hyperparameters.

B. Simulatability.

A model is said to be simulatable if a human (for whom the interpretation is intended) is able to internally simulate and reason about its entire decision-making process (i.e., how a trained model produces an output for an arbitrary input). This is a very strong constraint to place on a model and can generally be done only when the number of features is low and the underlying relationship is simple. Decision trees (38) are often cited as a simulatable model, due to their hierarchical decision-making process. Another example is lists of rules (39, 40), which can easily be simulated. However, it is important to note that these models cease to be simulatable when they become large. In particular, as the complexity of the model increases (number of nodes in a decision tree or the number of rules in a list), it becomes increasingly difficult for a human to internally simulate.

Due to their simplicity, simulatable models have very high descriptive accuracy. When they can also provide reasonable predictive accuracy, they can be very effective. In the following example, a simulatable model is able to produce high predictive accuracy, while maintaining the high levels of descriptive accuracy and relevancy normally attained by small-scale rules-based models.

Ex:

In medical practice, when a patient has been diagnosed with atrial fibrillation, caregivers often want to predict the risk that the particular patient will have a stroke in the next year. Given the potential ramifications of medical decisions, it is important that these predictions are not only accurate, but interpretable to both the caregivers and patients.

To make the prediction, ref. 40 uses data from 12,586 patients detailing their age, gender, history of drugs and conditions, and whether they had a stroke within 1 y of diagnosis. To construct a model that has high predictive and descriptive accuracy, ref. 40 introduces a method for learning lists of if–then rules that are predictive of 1-y stroke risk. The resulting classifier, displayed in SI Appendix, Fig. S1, requires only 7 if–then statements to achieve competitive accuracy and is easy for even nontechnical practitioners to quickly understand.

Although this model is able to achieve high predictive and descriptive accuracy, it is important to note that the lack of stability in these types of models can limit their uses. If the practitioner’s intent is to simply understand a model that is ultimately used for predictions, these types of models can be very effective. However, if the practitioner wants to produce knowledge about the underlying dataset, the fact that the learned rules can change significantly when the model is retrained limits their generalizability.

C. Modularity.

We define an ML model to be modular if a meaningful portion(s) of its prediction-making process can be interpreted independently. A wide array of models satisfies modularity to different degrees. Generalized additive models (41) force the relationship between variables in the model to be additive. In deep learning, specific methods such as attention (42) and modular network architectures (43) provide limited insight into a network’s inner workings. Probabilistic models can enforce modularity by specifying a conditional independence structure which makes it easier to reason about different parts of a model independently (44).

The following example uses modularity to produce relevant interpretations for use in diagnosing biases in training data.

Ex:

When prioritizing patient care for patients with pneumonia in a hospital, one possible method is to predict the likelihood of death within 60 d and focus on the patients with a higher mortality risk. Given the potential life and death consequences, being able to explain the reasons for hospitalizing a patient or not is very important.

A recent study (7) uses a dataset of 14,199 patients with pneumonia, with 46 features including demographics (e.g., age and gender), simple physical measurements (e.g., heart rate, blood pressure), and laboratory tests (e.g., white blood cell count, blood urea nitrogen). To predict mortality risk, the researchers use a generalized additive model with pairwise interactions, displayed below. The univariate and pairwise terms (fj(xj) and fij(xi,xj)) can be individually interpreted in the form of curves and heatmaps, respectively:

g(E[y])=β0+∑jfj(xj)+∑i≠jfij(xi,xj). [1]

By inspecting the individual modules, the researchers found a number of counterintuitive properties of their model. For instance, the fitted model learned that having asthma is associated with a lower risk of dying from pneumonia. In reality, the opposite is true—patients with asthma are known to have a higher risk of death from pneumonia. Because of this, in the collected data all patients with asthma received aggressive care, which was fortunately effective at reducing their risk of mortality relative to the general population.

In this instance, if the model were used without having been interpreted, pneumonia patients with asthma would have been deprioritized for hospitalization. Consequently, the use of ML would increase their likelihood of dying. Fortunately, the use of an interpretable model enabled the researchers to identify and correct errors like this one, better ensuring that the model could be trusted in the real world.

D. Domain-Based Feature Engineering.

While the type of model is important in producing a useful interpretation, so are the features that are used as inputs to the model. Having more informative features makes the relationship that needs to be learned by the model simpler, allowing one to use other model-based interpretability methods. Moreover, when the features have more meaning to a particular audience, they become easier to interpret.

In many individual domains, expert knowledge can be useful in constructing feature sets that are useful for building predictive models. The particular algorithms used to extract features are generally domain specific, relying both on the practitioner’s existing domain expertise and on insights drawn from the data through exploratory data analysis. For example, in natural language processing, documents are embedded into vectors using tf-idf (45). Moreover, using ratios, such as the body mass index (BMI), instead of raw features can greatly simplify the relationship a model learns, resulting in improved interpretations. In the example below, domain knowledge about cloud coverage is exploited to design 3 simple features that increase predictive accuracy while maintaining the high descriptive accuracy of a simple predictive model.

Ex:

When modeling global climate patterns, an important quantity is the amount and location of arctic cloud coverage. Due to the complex, layered nature of climate models, it is beneficial to have simple, easily auditable, cloud coverage models for use by downstream climate scientists.

In ref. 46, the authors use an unlabeled dataset of arctic satellite imagery to build a model predicting whether each pixel in an image contains clouds or not. Given the qualitative similarity between ice and clouds, this is a challenging prediction problem. By conducting exploratory data analysis and using domain knowledge through interactions with climate scientists, the authors identify 3 simple features that are sufficient to cluster whether or not images contain clouds. Using these 3 features as input to quadratic discriminant analysis, they achieve both high predictive accuracy and transparency when compared with expert labels (which were not used in developing the model).

E. Model-Based Feature Engineering.

There are a variety of automatic approaches for constructing interpretable features. Two examples are unsupervised learning and dimensionality reduction. Unsupervised methods, such as clustering, matrix factorization, and dictionary learning, aim to process unlabeled data and output a description of their structure. These structures often shed insight into relationships contained within the data and can be useful in building predictive models. Dimensionality reduction focuses on finding a representation of the data which is lower dimensional than the original data. Methods such as principal components analysis (47), independent components analysis (48), and canonical correlation analysis (49) can often identify a few interpretable dimensions, which can then be used as input to a model or to provide insights in their own right. Using fewer inputs can not only improve descriptive accuracy, but also increase predictive accuracy by reducing the number of parameters to fit. In the following example, unsupervised learning is used to represent images in a low-dimensional, genetically meaningful, space.

Ex:

Heterogeneity is an important consideration in genomic problems and associated data. In many cases, regulatory factors or biomolecules can play a specific role in one context, such as a particular cell type or developmental stage, and have a very different role in other contexts. Thus, it is important to understand the “local” behavior of regulatory factors or biomolecules. A recent study (50) uses unsupervised learning to learn spatial patterns of gene expression in Drosophila (fruit fly) embryos. In particular, it uses stability-driven nonnegative matrix factorization to decompose images of complex spatial gene expression patterns into a library of 21 “principal patterns,” which can be viewed as preorgan regions. This decomposition, which is interpretable to biologists, allows the study of gene–gene interactions in preorgan regions of the developing embryo.

6. Post Hoc Interpretability

We now discuss how interpretability considerations come into play in the post hoc analysis stage of the data–science life cycle. At this stage, the practitioner analyzes a trained model to provide insights into the learned relationships. This is particularly challenging when the model’s parameters do not clearly show what relationships the model has learned. To aid in this process, a variety of post hoc interpretability methods have been developed to provide insight into what a trained model has learned, without changing the underlying model. These methods are particularly important for settings where the collected data are high dimensional and complex, such as with image data. In these settings, interpretation methods must deal with the challenge that individual features are not semantically meaningful, making the problem more challenging than on datasets with more meaningful features. Once the information has been extracted from the fitted model, it can be analyzed using standard, exploratory data analysis techniques, such as scatter plots and histograms.

When conducting post hoc analysis, the model has already been trained, so its predictive accuracy is fixed. Thus, under the PDR framework, a researcher must consider only descriptive accuracy and relevancy (relative to a particular audience). Improving on each of these criteria are areas of active research.

Most widely useful post hoc interpretation methods fall into 2 main categories: prediction-level and dataset-level interpretations, which are sometimes referred to as local and global interpretations, respectively. Prediction-level interpretation methods focus on explaining individual predictions made by models, such as what features and/or interactions led to the particular prediction. Dataset-level approaches focus on the global relationships the model has learned, such as what visual patterns are associated with a predicted response. These 2 categories have much in common (in fact, dataset-level approaches often yield information at the prediction level), but we discuss them separately, as methods at different levels are meaningfully different. Prediction-level insights can provide fine-grained information about individual predictions, but often fail to yield dataset-level insights when it is not feasible to examine a sufficient amount of prediction-level interpretations.

A. Dataset-Level Interpretation.

When practitioners are interested in more general relationships learned by a model, e.g., relationships that are relevant for a particular class of responses, they use dataset-level interpretations. For instance, this form of interpretation can be useful when it is not feasible for a practitioner to look at a large number of local predictions. In addition to the areas below, we note that there are other emerging techniques, such as model distillation (51, 52).

A.1. Interaction and feature importances.

Feature importance scores, at the dataset level, try to capture how much individual features contribute, across a dataset, to a prediction. These scores can provide insights into what features the model has identified as important for which outcomes and their relative importance. Methods have been developed to score individual features in many models including neural networks (53), random forests, (54, 55), and generic classifiers (56).

In addition to feature importances, methods exist to extract important interactions between features. Interactions are important as ML models are often highly nonlinear and learn complex interactions between features. Methods exist to extract interactions from many ML models, including random forests (21, 57, 58) and neural networks (59, 60). In the below example, the descriptive accuracy of random forests is increased by extracting Boolean interactions (a problem-relevant form of interpretation) from a trained model.

Ex:

High-order interactions among regulatory factors or genes play an important role in defining cell type-specific behavior in biological systems. Thus, extracting such interactions from genomic data is an important problem in biology.

A previous line of work considers the problem of searching for biological interactions associated with important biological processes (21, 57). To identify candidate biological interactions, the authors train a series of iteratively reweighted random forests (RFs) and search for stable combinations of features that frequently co-occur along the predictive RF decision paths. This approach takes a step beyond evaluating the importance of individual features in an RF, providing a more complete description of how features influence predicted responses. By interpreting the interactions used in RFs, the researchers identified gene–gene interactions with 80% accuracy in the Drosophila embryo and identify candidate targets for higher-order interactions.

A.2. Statistical feature importances.

In some instances, in addition to the raw value, we can compute statistical measures of confidence as feature importance scores, a standard technique taught in introductory statistics classes. By making assumptions about the underlying data-generating process, models like linear and logistic regression can compute confidence intervals and hypothesis tests for the values, and linear combinations, of their coefficients. These statistics can be helpful in determining the degree to which the observed coefficients are statistically significant. It is important to note that the assumptions of the underlying probabilistic model must be fully verified before using this form of interpretation. Below we present a cautionary example where different assumptions lead to opposing conclusions being drawn from the same dataset.

Ex:

Here, we consider the lawsuit Students for Fair Admissions, Inc. v. Harvard regarding the use of race in undergraduate admissions to Harvard University. Initial reports by Harvard’s Office of Institutional Research used logistic regression to model the probability of admission using different features of an applicant’s profile, including race (61). This analysis found that the coefficient associated with being Asian (and not low income) was −0.418 with a significant P value (<0.001). This negative coefficient suggested that being Asian had a significant negative association with admission probability.

Subsequent analysis from both sides in the lawsuit attempted to analyze the modeling and assumptions to decide on the significance of race in the model’s decision. The plaintiff’s expert report (62) suggested that race was being unfairly used by building on the original report from Harvard’s Office of Institutional Research. It also incorporates analysis on more subjective factors such as “personal ratings” which seem to hurt Asian students’ admission. In contrast, the expert report supporting Harvard University (63) finds that by accounting for certain other variables, the effect of race on Asian students’ acceptance is no longer significant. Significances derived from statistical tests in regression or logistic regression models at best establish association, but not causation. Hence the analyses from both sides are flawed. This example demonstrates the practical and misleading consequences of statistical feature importances when used inappropriately.

A.3. Visualizations.

When dealing with high-dimensional datasets, it can be challenging to quickly understand the complex relationships that a model has learned, making the presentation of the results particularly important. To help deal with this, researchers have developed a number of different visualizations which help to understand what a model has learned. For linear models with regularization, plots of regression coefficient paths show how varying a regularization parameter affects the fitted coefficients. When visualizing convolutional neural networks trained on image data, work has been done on visualizing filters (64, 65), maximally activating responses of individual neurons or classes (66), understanding intraclass variation (67), and grouping different neurons (68). For long short-term memory networks (LSTMs), researchers have focused on analyzing the state vector, identifying individual dimensions that correspond to meaningful features (e.g., position in line, within quotes) (69), and building tools to track the model’s decision process over the course of a sequence (70).

In the following example, relevant interpretations are produced by using maximal activation images for identifying patterns that drive the response of brain cells.

Ex:

A recent study visualizes learned information from deep neural networks to understand individual brain cells (25). In this study, macaque monkeys were shown images while the responses of brain cells in their visual system (area V4) were recorded. Neural networks were trained to predict the responses of brain cells to the images. These neural networks produce accurate fits, but provide little insight into what patterns in the images increase the brain cells’ response without further analysis. To remedy this, the authors introduce DeepTune, a method which provides a visualization, accessible to neuroscientists and others, of the patterns which activate a brain cell. The main intuition behind the method is to optimize the input of a network to maximize the response of a neural network model (which represents a brain cell).

The authors go on to analyze the major problem of instability. When post hoc visualizations attempt to answer scientific questions, the visualizations must be stable to reasonable perturbations; if there are changes in the visualization due to the choice of a model, it is likely not meaningful. The authors address this explicitly by fitting 18 different models to the data and using a stable optimization over all of the models to produce a final consensus DeepTune visualization.

When interpreting the performance of an ML model, it can be helpful to look not just at the average accuracy, but also at the distribution of predictions and errors. For example, residual plots can identify heterogeneity in predictions and suggest particular data points to analyze, such as outliers in the predictions, or examples which had the largest prediction errors. Moreover, these plots can be used to analyze trends across the predictions. For instance, in the example below, influence functions are able to efficiently identify mislabeled data points.

B. Prediction-Level Interpretation.

Prediction-level approaches are useful when a practitioner is interested in understanding how individual predictions are made by a model. Note that prediction-level approaches can sometimes be aggregated to yield dataset-level insights.

B.1. Feature importance scores.

The most popular approach to prediction-level interpretation has involved assigning importance scores to individual features. Intuitively, a variable with a large positive (negative) score made a highly positive (negative) contribution to a particular prediction. In the deep learning literature, a number of different approaches have been proposed to address this problem (71–78), with some methods for other models as well (79). These are often displayed in the form of a heatmap highlighting important features. Note that feature importance scores at the prediction level can offer much more information than feature importance scores at the dataset level. This is a result of heterogeneity in a nonlinear model: The importance of a feature can vary for different examples as a result of interactions with other features.

While this area has seen progress in recent years, concerns have been raised about the descriptive accuracy of these methods. In particular, ref. 80 shows that many popular methods produce similar interpretations for a trained model versus a randomly initialized one and are qualitatively very similar to an edge detector. Moreover, it has been shown that some feature importance scores for CNNs are doing (partial) image recovery which is unrelated to the network decisions (81).

Ex:

When using ML models to predict sensitive outcomes, such as whether a person should receive a loan or a criminal sentence, it is important to verify that the algorithm is not discriminating against people based on protected attributes, such as race or gender. This problem is often described as ensuring ML models are “fair.” In ref. 17, the authors introduce a variable importance measure designed to isolate the contributions of individual variables, such as gender, among a set of correlated variables.

Based on these variable importance scores, the authors construct transparency reports, such as the one displayed in SI Appendix, Fig. S2, which displays the importance of features used to predict that “Mr. Z” is likely to be arrested in the future (an outcome which is often used in predictive policing), with each bar corresponding to a feature provided to the classifier, and the y axis displaying the importance score for that feature. In this instance, the race feature is the largest value, indicating that the classifier is indeed discriminating based on race. Thus, in this instance, prediction-level feature importance scores can identify that a model is unfairly discriminating based on race.

B.2. Alternatives to feature importances.

While feature importance scores can provide useful insights, they also have a number of limitations (80, 82). For instance, they are unable to capture when algorithms learn interactions between variables. There is currently an evolving body of work centered around uncovering and addressing these limitations. These methods focus on explicitly capturing and displaying the interactions learned by a neural network (83, 84), alternative forms of interpretations such as textual explanations (85), influential data points (86), and analyzing nearest neighbors (87, 88).

7. Future Work

Having introduced the PDR framework for defining and discussing interpretable machine learning, we now leverage it to frame what we feel are the field’s most important challenges moving forward. Below, we present open problems tied to each of this paper’s 3 main sections: interpretation desiderata (Section 4), model-based interpretability (Section 5), and post hoc interpretability (Section 6).

A. Measuring Interpretation Desiderata.

Currently, there is no clear consensus in the community around how to evaluate interpretation methods, although some recent works have begun to address it (12–14). As a result, the standard of evaluation varies considerably across different works, making it challenging both for researchers in the field to measure progress and for prospective users to select suitable methods. Within the PDR framework, to constitute an improvement, an interpretation method must improve at least one desideratum (predictive accuracy, descriptive accuracy, or relevancy) without unduly harming the others. While improvements in predictive accuracy are easy to measure, measuring improvements in descriptive accuracy and relevancy remains a challenge.

A.1. Measuring descriptive accuracy.

One way to measure an improvement to an interpretation method is to demonstrate that its output better captures what the ML model has learned, i.e., its descriptive accuracy. However, unlike predictive accuracy, descriptive accuracy is generally very challenging to measure or quantify (82). As a fallback, researchers often show individual, cherry-picked, interpretations which seem “reasonable.” These kinds of evaluations are limited and unfalsifiable. In particular, these results are limited to the few examples shown and not generally applicable to the entire dataset.

While the community has not settled on a standard evaluation protocol, there are some promising directions. In particular, the use of simulation studies presents a partial solution. In this setting, a researcher defines a simple generative process, generates a large amount of data from that process, and trains the ML model on those data. Assuming a proper simulation setup, a sufficiently powerful model to recover the generative process, and sufficiently large training data, the trained model should achieve near-perfect generalization accuracy. To compute an evaluation metric, the researcher can then check whether the interpretations recover aspects of the original generative process. For example, refs. 59 and 89 train neural networks on a suite of generative models with certain built-in interactions and test whether their method successfully recovers them. Here, due to the ML model’s near-perfect generalization accuracy, we know that the model is likely to have recovered some aspects of the generative process, thus providing a ground truth against which to evaluate interpretations. In a related approach, when an underlying scientific problem has been previously studied, prior experimental findings can serve as a partial ground truth to retrospectively validate interpretations (21).

A.2. Demonstrating relevancy to real-world problems.

Another angle for developing improved interpretation methods is to improve the relevancy of interpretations for some audience or problem. This is normally done by introducing a novel form of output, such as feature heatmaps (71), rationales (90), or feature hierarchies (84), or identifying important elements in the training set (86). A common pitfall in the current literature is to focus on the novel output, ignoring what real-world problems it can actually solve. Given the abundance of possible interpretations, it is particularly easy for researchers to propose novel methods which do not actually solve any real-world problems.

There have been 2 dominant approaches for demonstrating improved relevancy. The first, and strongest, is to directly use the introduced method in solving a domain problem. For instance, in one example discussed above (21), the authors evaluated a new interpretation method (iterative random forests) by demonstrating that it could be used to identify meaningful biological Boolean interactions for use in experiments. In instances like this, where the interpretations are used directly to solve a domain problem, their relevancy is indisputable. A second, less direct, approach is the use of human studies, often through services like Amazon’s Mechanical Turk. Here, humans are asked to perform certain tasks, such as evaluating how much they trust a model’s predictions (84). While challenging to properly construct and perform, these studies are vital to demonstrate that new interpretation methods are, in fact, relevant to any potential practitioners. However, one shortcoming of this approach is that it is only possible to use a general audience of AMT crowdsourced workers, rather than a more relevant, domain-specific audience.

B. Model Based.

Now that we have discussed the general problem of evaluating interpretations, we highlight important challenges for the 2 main subfields of interpretable machine learning: model-based and post hoc interpretability. Whenever model-based interpretability can achieve reasonable predictive accuracy and relevancy, by virtue of its high descriptive accuracy it is preferable to fitting a more complex model and relying upon post hoc interpretability. Thus, the main focus for model-based interpretability is increasing its range of possible use cases by increasing its predictive accuracy through more accurate models and transparent feature engineering. It is worth noting that sometimes a combination of model-based and post hoc interpretations is ideal.

B.1. Building accurate and interpretable models.

In many instances, model-based interpretability methods fail to achieve a reasonable predictive accuracy. In these cases, practitioners are forced to abandon model-based interpretations in search of more accurate models. Thus, an effective way of increasing the potential uses for model-based interpretability is to devise new modeling methods which produce higher predictive accuracy while maintaining their high descriptive accuracy and relevance. Promising examples of this work include the previously discussed examples on estimating pneumonia risk from patient data (7) and Bayesian models for generating rule lists to estimate a patient’s risk of stroke (40). Detailed directions for this work are suggested in ref. 91.

B.2. Tools for feature engineering.

When we have more informative and meaningful features, we can use simpler modeling methods to achieve a comparable predictive accuracy. Thus, methods that can produce more useful features broaden the potential uses of model-based interpretations. The first main category of work lies in improved tools for exploratory data analysis. By better enabling researchers to interact with and understand their data, these tools (combined with domain knowledge) provide increased opportunities for them to identify helpful features. Examples include interactive environments (92–94), tools for visualization (95–97), and data exploration tools (98, 99). The second category falls under unsupervised learning, which is often used as a tool for automatically finding relevant structure in data. Improvements in unsupervised techniques such as clustering and matrix factorization could lead to more useful features.

C. Post Hoc.

In contrast to model-based interpretability, much of post hoc interpretability is relatively new, with many foundational concepts still unclear. In particular, we feel that 2 of the most important questions to be answered are what an interpretation of an ML model should look like and how post hoc interpretations can be used to increase a model’s predictive accuracy. It has also been emphasized that in high-stakes decisions practitioners should be very careful when applying post hoc methods with unknown descriptive accuracy (91).

C.1. What an interpretation of a black box should look like.

Given a black-box predictor and real-world problem, it is generally unclear what format, or combination of formats, is best to fully capture a model’s behavior. Researchers have proposed a variety of interpretation forms, including feature heatmaps (71), feature hierarchies (84), and identifying important elements in the training set (86). However, in all instances there is a gap between the simple information provided by these interpretations and what the model has actually learned. Moreover, it is unclear whether any of the current interpretation forms can fully capture a model’s behavior or whether a new format altogether is needed. How to close that gap, while producing outputs relevant to a particular audience/problem, is an open problem.

C.2. Using interpretations to improve predictive accuracy.

In some instances, post hoc interpretations uncover that a model has learned relationships a practitioner knows to be incorrect. For instance, prior interpretation work has shown that a binary husky vs. wolf classifier simply learns to identify whether there is snow in the image, ignoring the animals themselves (77). A natural question to ask is whether it is possible for the practitioner to correct these relationships learned by the model and consequently increase its predictive accuracy. Given the challenges surrounding simply generating post hoc interpretations, research on their uses has been limited (100, 101), particularly in modern deep learning models. However, as the field of post hoc interpretations continues to mature, this could be an exciting avenue for researchers to increase the predictive accuracy of their models by exploiting prior knowledge, independently of any other benefits of interpretations.

Supplementary Material

Supplementary File

Acknowledgments

This research was supported in part by Grants Army Research Office W911NF1710005, Office of Naval Research N00014-16-1-2664, National Science Foundation (NSF) DMS-1613002, and NSF IIS 1741340; an Natural Sciences and Engineering Research Council of Canada Postgraduate Scholarships-Doctoral program fellowship; and an Adobe research award. We thank the Center for Science of Information, a US NSF Science and Technology Center, under Grant CCF-0939370. R.A.-A. thanks the Allen Institute founder, Paul G. Allen, for his vision, encouragement, and support.

Footnotes

The authors declare no competing interest.

*For clarity, throughout this paper we use the term “model” to refer to both machine-learning models and algorithms.

†Examples were selected through a nonexhaustive search of related work.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File