Noise-based switches and amplifiers for gene expression - PubMed (original) (raw)

Noise-based switches and amplifiers for gene expression

J Hasty et al. Proc Natl Acad Sci U S A. 2000.

Abstract

The regulation of cellular function is often controlled at the level of gene transcription. Such genetic regulation usually consists of interacting networks, whereby gene products from a single network can act to control their own expression or the production of protein in another network. Engineered control of cellular function through the design and manipulation of such networks lies within the constraints of current technology. Here we develop a model describing the regulation of gene expression and elucidate the effects of noise on the formulation. We consider a single network derived from bacteriophage lambda and construct a two-parameter deterministic model describing the temporal evolution of the concentration of lambda repressor protein. Bistability in the steady-state protein concentration arises naturally, and we show how the bistable regime is enhanced with the addition of the first operator site in the promotor region. We then show how additive and multiplicative external noise can be used to regulate expression. In the additive case, we demonstrate the utility of such control through the construction of a protein switch, whereby protein production is turned "on" and "off" by using short noise pulses. In the multiplicative case, we show that small deviations in the transcription rate can lead to large fluctuations in the production of protein, and we describe how these fluctuations can be used to amplify protein production significantly. These results suggest that an external noise source could be used as a switch and/or amplifier for gene expression. Such a development could have important implications for gene therapy.

PubMed Disclaimer

Figures

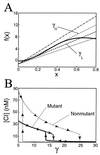
Figure 1

Figure 1

Bifurcation plots for the variable x and concentration of λ repressor. (A) Graphical depiction of the fixed points of Eq. 7, generated by setting ẋ = 0 and plotting α x_2/(1 + 2_x_2 + 5_x_4) and the line γ_x − 1. As the slope γ is increased, the system traverses a region of multistability and returns to a state of monostability. (B) Hysterisis loops for the mutant and nonmutant systems obtained by setting ẋ = 0 in Eqs. 7 and 8. Beginning with concentrations of 35 nM for the mutant system and 85 nM for the nonmutant system, we steadily increase the degradation parameter γ. In both systems, the concentration of repressor slowly decreases until a bifurcation point. In the mutant (nonmutant) system, the repressor concentration abruptly drops to a lower value at γ ∼ 16 (γ ∼ 24). Then, on reversing course and decreasing γ, the repressor concentration increases slowly until γ encounters a second bifurcation point at γ ∼ 14 (γ ∼ 6), whereby the concentration immediately jumps to a value of 15 nM (mutant) or 70 nM (nonmutant). The subsequent hysterisis loop is approximately 10 times larger in the nonmutant case. Parameter values are α = 50, _K_1 = 0.05 nM−1, and _K_2 = 0.026 nM−1 for the mutant system, and _K_2 = 0.033 nM−1 for the nonmutant system (12, 13).

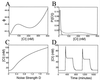
Figure 2

Figure 2

Results for additive noise with parameter values α = 10 and γ = 5.5. (A) The energy landscape. Stable equilibrium concentration values of Eq. 8 correspond to the valleys at [CI] = 10 and 200 nM, with an unstable value at [CI] = 99 nM. (B) Steady-state probability distributions for noise strengths of D = 0.04 (solid line) and D = 0.4 (dotted line). (C) The steady-state equilibrium protein concentration plotted vs. noise strength. The concentration increases as the noise causes the upper state of A to become increasingly populated. (D) Simulation of Eq. 9 demonstrating the utilization of external noise for protein switching. Initially, the concentration begins at a level of [CI] = 10 nM corresponding to a low noise value of D = 0.01. After 6 hr, a large 30-min noise pulse of strength D = 1.0 is used to drive the concentration to 58 nM. After this pulse, the noise is returned to its original value. At 11 hr, a smaller 90-min noise pulse of strength D = 0.04 is used to return the concentration to near its original value. The simulation technique is that of ref. .

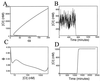
Figure 3

Figure 3

Results for multiplicative noise. (A) Bifurcation plot for the repressor concentration vs. the model parameter α. The steep upper branch implies that modest fluctuations in α will cause large fluctuations around the upper fixed value of repressor concentration, whereas the flat lower branch implies small fluctuations about the lower value. (B) The evolution of the repressor concentration in a single colony, obtained by simulation of Eq. 14. Relatively small random variations of the parameter α (∼6%) induce large fluctuations in the steady-state concentration until around 700 min and small fluctuations thereafter. (C) Energy landscape for parameter values α = 100 and γ = 8.5. (D) Large-scale amplification of the protein concentration obtained by simulation of Eq. 14. At 20 hr, a 60-min noise pulse of strength D = 1.0 is used to quickly increase the protein concentration by over three orders of magnitude. The parameter values are the same as those in C.

Similar articles

Cited by

References

    1. Dickson R, Abelson J, Barnes W. Science. 1975;187:27–35. - PubMed
    1. Yuh C H, Bolouri H, Davidson E H. Science. 1998;279:1896–1902. - PubMed
    1. Lewin B. Genes VI. Oxford: Oxford Univ. Press; 1997.
    1. Harada Y, Funatsu T, Murakami K, Nonoyama Y, Ishihama A, Yarnagida T. Biophys J. 1999;76:709–715. - PMC - PubMed
    1. McAdams H H, Arkin A. Proc Natl Acad Sci USA. 1997;94:814–819. - PMC - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources