Extending unbiased stereology of brain ultrastructure to three-dimensional volumes - PubMed (original) (raw)
Extending unbiased stereology of brain ultrastructure to three-dimensional volumes
J C Fiala et al. J Am Med Inform Assoc. 2001 Jan-Feb.
Abstract
Objective: Analysis of brain ultrastructure is needed to reveal how neurons communicate with one another via synapses and how disease processes alter this communication. In the past, such analyses have usually been based on single or paired sections obtained by electron microscopy. Reconstruction from multiple serial sections provides a much needed, richer representation of the three-dimensional organization of the brain. This paper introduces a new reconstruction system and new methods for analyzing in three dimensions the location and ultrastructure of neuronal components, such as synapses, which are distributed non-randomly throughout the brain.
Design and measurements: Volumes are reconstructed by defining transformations that align the entire area of adjacent sections. Whole-field alignment requires rotation, translation, skew, scaling, and second-order nonlinear deformations. Such transformations are implemented by a linear combination of bivariate polynomials. Computer software for generating transformations based on user input is described. Stereological techniques for assessing structural distributions in reconstructed volumes are the unbiased bricking, disector, unbiased ratio, and per-length counting techniques. A new general method, the fractional counter, is also described. This unbiased technique relies on the counting of fractions of objects contained in a test volume. A volume of brain tissue from stratum radiatum of hippocampal area CA1 is reconstructed and analyzed for synaptic density to demonstrate and compare the techniques.
Results and conclusions: Reconstruction makes practicable volume-oriented analysis of ultrastructure using such techniques as the unbiased bricking and fractional counter methods. These analysis methods are less sensitive to the section-to-section variations in counts and section thickness, factors that contribute to the inaccuracy of other stereological methods. In addition, volume reconstruction facilitates visualization and modeling of structures and analysis of three-dimensional relationships such as synaptic connectivity.
Figures
Figure 1
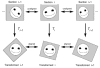
Alignment of serial section images in absolute mode. The original section images (top row) are unaligned. After applying the appropriate transformation (T) to each section image, the resulting transformed section images are all in alignment (bottom row).
Figure 2
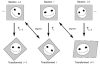
Incremental alignment of serial section images. The original section images (top row) are unaligned. After applying the appropriate transformation (T i) to section i, the resulting transformed image is in alignment with the original image of section i–1. Likewise, the transformed section i+1 is in alignment with the untransformed section i. Since each alignment is independent of alignments between other sections, incremental alignments allow easy modification of alignments. Ultimately, the incremental alignment is converted to an absolute alignment for analysis.
Figure 3
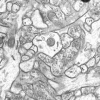
Blended images from two adjacent serial sections. Left, When sections are in good alignment, objects are clear because object boundaries overlie each other. Right, When sections are misaligned, the image is blurry because of the doubling of object boundaries.
Figure 3
Blended images from two adjacent serial sections. Left, When sections are in good alignment, objects are clear because object boundaries overlie each other. Right, When sections are misaligned, the image is blurry because of the doubling of object boundaries.
Figure 4
A sequence (from upper left to lower right) of six serial sections that pass longitudinally through a mitochondrion (M). At the central section, the diameter (d) is measured. Since the mitochondrion is cylindric, the ratio of the diameter to the number of sections spanned by the mitochondrion is an estimate of section thickness. On the first and last section, the mitochondrion may appear as a gray wall at the point where the diameter was measured. In such cases, depending on the darkness of the gray wall, a fractional value of either 0.25, 0.5, or 0.75 is used instead of the full section count. For the case shown, the mitochondrion spans four sections fully and about 0.25 sections at either end, for a thickness estimate of d/4.5.
Figure 5
Two-dimensional sampling from a grid of rectangular frames. Left, A grid of two-dimensional sampling frames is placed over an area (_A_ref, light gray) containing profiles (white) to be counted. A single sampling frame (A f, dark gray) of the grid with its exclusion lines (bold). Profiles contacting the frame are counted (hashed profile) unless the profiles contact an exclusion line. Thus, for the shaded frame, only one profile is counted. Right, Bias due to edging profiles. When the extended exclusion lines are not used, there is bias due the profiles that intersect the boundary of the sampling frame. When all edging profiles are counted (upper curve), there is much more error than when profiles intersecting two edges are excluded (lower curve). Curves were generated from the ratio of sampled to frame areas with the assumption of a square frame and circular profiles. Frame size refers to the width of the frame square. Profile size can be interpreted as the diameter of a circle needed to contain the largest profile in the reference area.
Figure 5
Two-dimensional sampling from a grid of rectangular frames. Left, A grid of two-dimensional sampling frames is placed over an area (_A_ref, light gray) containing profiles (white) to be counted. A single sampling frame (A f, dark gray) of the grid with its exclusion lines (bold). Profiles contacting the frame are counted (hashed profile) unless the profiles contact an exclusion line. Thus, for the shaded frame, only one profile is counted. Right, Bias due to edging profiles. When the extended exclusion lines are not used, there is bias due the profiles that intersect the boundary of the sampling frame. When all edging profiles are counted (upper curve), there is much more error than when profiles intersecting two edges are excluded (lower curve). Curves were generated from the ratio of sampled to frame areas with the assumption of a square frame and circular profiles. Frame size refers to the width of the frame square. Profile size can be interpreted as the diameter of a circle needed to contain the largest profile in the reference area.
Figure 6
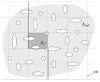
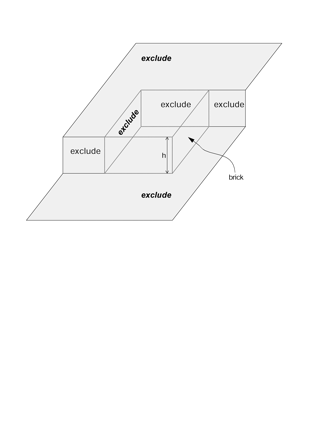
Extension of the sampling frame concept to three dimensions produces a “brick” in the shape of a rectangular prism (dashed outline). The brick is bordered by exclusion planes (labeled “exclude”) on three sides. Objects intersecting the bottom of the brick are excluded, as are objects intersecting the back or left side of the brick. In addition, there are exclusion regions adjacent to the front and top faces of the brick. The top, front, and right side of the brick are inclusion faces. The brick has height h perpendicular to the plane of sectioning.
Figure 7
Each object's profile (O i) has a fraction (α_i_) that lies inside a test frame with area A f. An unbiased estimate of profile density can be computed by counting these fractions.
Figure 8
A serially sectioned object appears as a single profile (bold ellipse) in the sampling frame (solid and dashed lines) placed into one of the sections. The object also has profiles that appear on adjacent sections (light ellipses). In total, the object has profiles that appear on s o number of sections. The object fraction within the section is 1/s o.
Figure 9
Sampling of a dendrite by a series of test regions of length l i. Each spine originating from the dendrite has a synapse (black). The hash marks at the top show that _l_1 is 3, _l_2 is 4, and _l_3 is 5 units long. For segment 2, the exclusion end is indicated by a dark line. The other end is the inclusion end (dashed line). Similar left exclusion ends and right inclusion ends are defined (but not shown) for the other segments. Using the counting rule described in the text, segment 1 has five spine origins, segment 2 has nine spine origins, and segment 3 has eight spine origins, so the number of spines per length (N L) is 22/10. Similarly, segment 1 has five synapses, segment 2 has ten synapses, and segment 3 has nine synapses, so N L is 24/10.
Figure 10
Sample volume reconstruction and analysis. Top, A section of the series showing the sampling frame (blue) and identified synapses (red). The left and top edges of the frame are exclusion edges. A synapse that contacts an exclusion edge is marked with a yellow contour. Bottom, The stack of serial sections for the aligned series is depicted in semi-transparent gray. After alignment, the sections form a volume with an irregular boundary due to the different transformations applied to each section. Inside this irregular volume, a rectangular prism or brick (purple) was defined as a reference volume for making density measurements.
Figure 10
Sample volume reconstruction and analysis. Top, A section of the series showing the sampling frame (blue) and identified synapses (red). The left and top edges of the frame are exclusion edges. A synapse that contacts an exclusion edge is marked with a yellow contour. Bottom, The stack of serial sections for the aligned series is depicted in semi-transparent gray. After alignment, the sections form a volume with an irregular boundary due to the different transformations applied to each section. Inside this irregular volume, a rectangular prism or brick (purple) was defined as a reference volume for making density measurements.
Figure 11
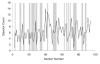
The distribution of disector counts through the reference volume. Each pair of sections in the series represents a disector of one section thickness. The solid line shows the count (_Q_–) obtained for each such disector. The gray bars show the random selection of 33 of the disectors for estimation of synaptic density.
Figure 12
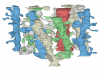
The set of 11 dendrite segments reconstructed from the volume. The dendrites appear in the three-dimensional configuration that they have in the reconstructed volume. They are colored to help distinguish the individual segments and their spines. The red dendrite is a segment from an interneuron as determined by the frequency and clustering of shaft synapses and the lack of mature-looking spines.
Comment in
- Human brain program research progress in bioinformatics/ neuroinformatics.
Wong ST, Koslow SH. Wong ST, et al. J Am Med Inform Assoc. 2001 Jan-Feb;8(1):103-4. doi: 10.1136/jamia.2001.0080103. J Am Med Inform Assoc. 2001. PMID: 11141517 Free PMC article. No abstract available.
Similar articles
- Complementary techniques for unbiased stereology of brain ultrastructure.
Marrone DF, LeBoutillier JC, Petit TL. Marrone DF, et al. J Electron Microsc (Tokyo). 2003;52(4):425-8. doi: 10.1093/jmicro/52.4.425. J Electron Microsc (Tokyo). 2003. PMID: 14599105 Review. - [Three-dimentional organization of synapses and astroglia in the hippocampus of rats and ground squirrels: new structural and functional paradigms of the synapse function].
Popov VI, Medvedev NI, Rogachevskiĭ VV, Ignat'ev DA, Stewart MG, Fesenko EE. Popov VI, et al. Biofizika. 2003 Mar-Apr;48(2):289-308. Biofizika. 2003. PMID: 12723356 Review. Russian. - Three-dimensional organization of cell adhesion junctions at synapses and dendritic spines in area CA1 of the rat hippocampus.
Spacek J, Harris KM. Spacek J, et al. J Comp Neurol. 1998 Mar 30;393(1):58-68. doi: 10.1002/(sici)1096-9861(19980330)393:1<58::aid-cne6>3.0.co;2-p. J Comp Neurol. 1998. PMID: 9520101 - [A computer-aided analysis system for counting the synaptic numerical density based on disector technique].
Shen L, Zhang L, Huang H, Liu H, Nan Y, Shang J, Liao H. Shen L, et al. Sheng Wu Yi Xue Gong Cheng Xue Za Zhi. 2000 Jun;17(2):167-9. Sheng Wu Yi Xue Gong Cheng Xue Za Zhi. 2000. PMID: 12557772 Chinese. - A resource from 3D electron microscopy of hippocampal neuropil for user training and tool development.
Harris KM, Spacek J, Bell ME, Parker PH, Lindsey LF, Baden AD, Vogelstein JT, Burns R. Harris KM, et al. Sci Data. 2015 Sep 1;2:150046. doi: 10.1038/sdata.2015.46. eCollection 2015. Sci Data. 2015. PMID: 26347348 Free PMC article.
Cited by
- Human Brain Program Research Progress in biomedical imaging/neuroscience, 2001.
Wong ST, Koslow SH. Wong ST, et al. J Am Med Inform Assoc. 2001 Sep-Oct;8(5):510-1. doi: 10.1136/jamia.2001.0080510. J Am Med Inform Assoc. 2001. PMID: 11522771 Free PMC article. No abstract available. - Apical organelle discharge by Cryptosporidium parvum is temperature, cytoskeleton, and intracellular calcium dependent and required for host cell invasion.
Chen XM, O'Hara SP, Huang BQ, Nelson JB, Lin JJ, Zhu G, Ward HD, LaRusso NF. Chen XM, et al. Infect Immun. 2004 Dec;72(12):6806-16. doi: 10.1128/IAI.72.12.6806-6816.2004. Infect Immun. 2004. PMID: 15557601 Free PMC article. - Ultrastructural heterogeneity of layer 4 excitatory synaptic boutons in the adult human temporal lobe neocortex.
Yakoubi R, Rollenhagen A, von Lehe M, Miller D, Walkenfort B, Hasenberg M, Sätzler K, Lübke JH. Yakoubi R, et al. Elife. 2019 Nov 20;8:e48373. doi: 10.7554/eLife.48373. Elife. 2019. PMID: 31746736 Free PMC article. - Differential Effects of Sevoflurane Exposure on Long-Term Fear Memory in Neonatal and Adult Rats.
Li C, Liu S, Mei Y, Wang Q, Lu X, Li H, Tao F. Li C, et al. Mol Neurobiol. 2022 May;59(5):2799-2807. doi: 10.1007/s12035-021-02629-x. Epub 2022 Feb 24. Mol Neurobiol. 2022. PMID: 35201592 - Rapid Neuronal Ultrastructure Disruption and Recovery during Spreading Depolarization-Induced Cytotoxic Edema.
Kirov SA, Fomitcheva IV, Sword J. Kirov SA, et al. Cereb Cortex. 2020 Sep 3;30(10):5517-5531. doi: 10.1093/cercor/bhaa134. Cereb Cortex. 2020. PMID: 32483593 Free PMC article.
References
- Jing Z, Sachs F. Alignment of tomographic projections using an incomplete set of fiducial markers. Ultramicroscopy. 1991;35:37–43. - PubMed
- Soto GE, Young SJ, Martone ME, et al. Serial section electron tomography: a method for three-dimensional reconstruction of large structures. Neuroimage. 1994;1:230–43. - PubMed
- Huijsmans DP, Lamers WH, Los JA, Strackee J. Toward computerized morphometric facilities: a review of 58 software packages for computer-aided three-dimensional reconstruction, quantification, and picture generation from parallel serial sections. Anat Rec. 1986;216:449–70. - PubMed
- Stevens JK, Davis TL, Freidman N, Sterling P. A systematic approach to reconstructing microcircuitry by electron microscopy of serial sections. Brain Res Rev. 1980;2:265–93. - PubMed
- Stevens JK, Trogadis J. Computer-assisted reconstruction from serial electron micrographs: a tool for the systematic study of neuronal form and function. Adv Cell Neurobiol. 1984;5:341–69.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous