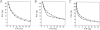Statistical potentials for fold assessment - PubMed (original) (raw)

Comparative Study

Statistical potentials for fold assessment

Francisco Melo et al. Protein Sci. 2002 Feb.

Abstract

A protein structure model generally needs to be evaluated to assess whether or not it has the correct fold. To improve fold assessment, four types of a residue-level statistical potential were optimized, including distance-dependent, contact, Phi/Psi dihedral angle, and accessible surface statistical potentials. Approximately 10,000 test models with the correct and incorrect folds were built by automated comparative modeling of protein sequences of known structure. The criterion used to discriminate between the correct and incorrect models was the Z-score of the model energy. The performance of a Z-score was determined as a function of many variables in the derivation and use of the corresponding statistical potential. The performance was measured by the fractions of the correctly and incorrectly assessed test models. The most discriminating combination of any one of the four tested potentials is the sum of the normalized distance-dependent and accessible surface potentials. The distance-dependent potential that is optimal for assessing models of all sizes uses both C(alpha) and C(beta) atoms as interaction centers, distinguishes between all 20 standard residue types, has the distance range of 30 A, and is derived and used by taking into account the sequence separation of the interacting atom pairs. The terms for the sequentially local interactions are significantly less informative than those for the sequentially nonlocal interactions. The accessible surface potential that is optimal for assessing models of all sizes uses C(beta) atoms as interaction centers and distinguishes between all 20 standard residue types. The performance of the tested statistical potentials is not likely to improve significantly with an increase in the number of known protein structures used in their derivation. The parameters of fold assessment whose optimal values vary significantly with model size include the size of the known protein structures used to derive the potential and the distance range of the accessible surface potential. Fold assessment by statistical potentials is most difficult for the very small models. This difficulty presents a challenge to fold assessment in large-scale comparative modeling, which produces many small and incomplete models. The results described in this study provide a basis for an optimal use of statistical potentials in fold assessment.

PubMed Disclaimer

Figures

Fig. 1.

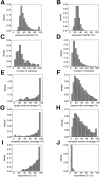
Fig. 1.

Properties of the good (left) and bad models (right). (A,B) Percentage sequence identity between the target and the template. (C,D) Model length. (E,F) Target chain coverage (the fraction of the target chain residues that were modeled). (G,H) Template domain coverage (the fraction of the template domain residues that were aligned to the target chain). The domain coverage was calculated using the domain definitions in the CATH database (Orengo et al. 1997). (I,J) Structural overlap between the target model and the actual target structure expressed as percentage of the equivalent Cα atoms (Materials and Methods).

Fig. 2.

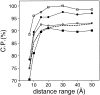
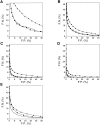
Fig. 2.

Performance of the distance-dependent potential as a function of its range. The percentage of the correctly predicted cases for the optimal Z-score cutoff (Materials and Methods). The performance is shown separately for the four sets with 100 good and 100 bad test models each (100/100 sets) (Materials and Methods): The very small models (▪), the small models (○), the medium size models (•), and the large models (□). The performance on the 400/400 test model set is indicated by the broken line. The potentials were calculated as specified in Table 1, except for the varying distance range.

Fig. 3.

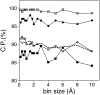
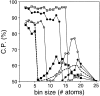
Fig. 3.

Performance of the distance-dependent potential as a function of its resolution (bin size). The potentials were calculated as specified in Table 1, except for the varying bin size. See the legend to Fig. 2 ▶ for information about the different test model sets represented by the different symbols.

Fig. 4.

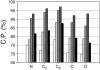
Fig. 4.

Performance of the distance-dependent potential as a function of its interaction centers. The atom types whose coordinates were used as the interaction centers are listed on the x-axes. The potentials were calculated as specified in Table 1 except for the varying interaction centers and the potential range of 15 Å. The results for the four 100/100 test sets with models of increasing size are indicated by bars of increasing darkness; the results for the 400/400 set of test models are indicated by the black bars.

Fig. 5.

Fig. 5.

Performance of the distance-dependent potential as a function of its range and sequence separation. (A) Potentials were derived from and used for assessing both the local (2 < k ≤ 8) and nonlocal (k ≥ 9) interactions. (B) Potentials were derived from and used for assessing only the nonlocal interactions. (C) Potentials were derived from and used for assessing only the local interactions. (D) Potentials were derived from the nonlocal interactions, but used to assess both the local and nonlocal interactions, irrespective of their k. See the legend to Fig. 2 ▶ for additional information about the potentials and the different test model sets represented by the different symbols.

Fig. 6.

Fig. 6.

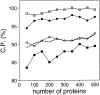
Performance of the distance-dependent potential as a function of the number of known protein structures used to extract the potential. The potentials were calculated from the 10 sets containing from 50 to 500 known structures (Materials and Methods), as specified in Table 1, except for the potential range of 15 Å. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

Fig. 7.

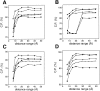
Fig. 7.

Performance of the distance-dependent potential as a function of its range and the size of the known structures used to calculate the potential. Four sets of known protein structures were used to extract the potentials: small (<100 residues; ○), medium (100–200 residues; •), large (>200 residues; ▪), and all (the sma-med-large set; broken line) (Materials and Methods). Model assessment by these potentials was evaluated separately for the four 100/100 very small (A), small (B), medium size (C), and large model test sets (D), as well as for the combined 400/400 test set (E) (Materials and Methods). The potentials were calculated as specified in Table 1.

Fig. 8.

Fig. 8.

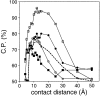
Performance of the contact potential as a function of its contact distance. The interaction centers were the Cβ atoms. All the contacts with k ≥ 2 were considered. The reference state used to calculate the potentials was other residues (Materials and Methods). The potentials were extracted from the sma-med-lar set of known protein structures. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

Fig. 9.

Fig. 9.

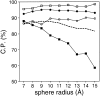
Performance of the accessible surface potential as a function of its distance range (sphere radius). The potentials were calculated as specified in Table 2, except for the burial range of 200 atoms and the varying sphere radius. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

Fig. 10.

Fig. 10.

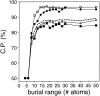
Performance of the accessible surface potential as a function of its burial range. The potentials were calculated as specified in Table 2, except for the varying burial range. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

Fig. 11.

Fig. 11.

Performance of the accessible surface potential as a function of its resolution (bin size). The potentials were calculated as specified in Table 2, except for the burial range of 30 atoms and the varying bin size. See the legend to Fig. 2 ▶ for the different test model sets represented by the different symbols.

Fig. 12.

Fig. 12.

Performance of the accessible surface potential as a function of its interaction centers. The potentials were calculated as specified in Table 2, except for the distance range of 10 Å and the varying interaction centers. See the legend to Fig. 4 ▶ for the different test model sets represented by the different bar shades.

Fig. 13.

Fig. 13.

Performance of the accessible surface potential as a function of its burial range and the size of the known structures used to calculate the potential. Four sets of known protein structures were used to extract the potentials: small (<100 residues; ○), medium (100–200 residues; •), large (>200 residues; □), and all (the sma-med-large set; broken line) (Materials and Methods). Model assessment by these potentials was evaluated separately for the four 100/100 very small (A), small (B), medium size (C), and large model test sets (D), as well as for the combined 400/400 test set (E) (Materials and Methods). The potentials were calculated as specified in Table 2.

Fig. 14.

Fig. 14.

Performance of the optimal distance-dependent, accessible surface, and combined statistical potentials. The performance is described by the ROC curves, which plot the fraction of false negatives (F.N.) as a function of the fraction of false positives (F.P.) (Materials and Methods). The lower the curve, the better the discrimination between the good and bad models. The ROC curves for the accessible surface potential (•), the distance dependent potential (▪), and the combined potential (broken line) are plotted. (A) The 443/1922 test set of the very small models, (B) the 1103/2600 test set of the small models, (C) the 1126/1412 test set of the medium size models, and (D) the 703/336 test set of the large models. (E) The performance of the potentials is also evaluated by the 3375/6270 set of all good and bad models.

Fig. 15.

Fig. 15.

Performance of the sequence space (•) and structure space (○) references for the calculation of the energy Z-scores. The predictive power is assessed for the 3375/6270 test model set. The statistical potentials and the polyprotein implemented in the program P

rosa

II were used (Sippl 1993). (A) Distance dependent potential. (B) Accessible surface potential. (C) The combined potential.

Similar articles

Cited by

References

    1. Abagyan, R. and Totrov, M. 1997. Contact area difference (CAD): A robust measure to evaluate accuracy of protein models. J. Mol. Biol. 268 678–685. - PubMed
    1. Altschul, S. 1998. Generalized affine gap costs for protein sequence alignment. Proteins 32 88–96. - PubMed
    1. Bahar, I. and Jernigan, R. 1997. Inter-residue potentials in globular proteins and the dominance of highly specific hydrophilic interactions at close separation. J. Mol. Biol. 266 195–214. - PubMed
    1. Baker, D. and Sali, A. 2001. Protein structure modeling and structural genomics. Science 294 93–96. - PubMed
    1. Bauer, A. and Beyer, A. 1994. An improved pair potential to recognize native protein folds. Proteins 18 254–261. - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources