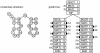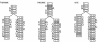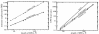A memory-efficient dynamic programming algorithm for optimal alignment of a sequence to an RNA secondary structure - PubMed (original) (raw)
Comparative Study
A memory-efficient dynamic programming algorithm for optimal alignment of a sequence to an RNA secondary structure
Sean R Eddy. BMC Bioinformatics. 2002.
Abstract
Background: Covariance models (CMs) are probabilistic models of RNA secondary structure, analogous to profile hidden Markov models of linear sequence. The dynamic programming algorithm for aligning a CM to an RNA sequence of length N is O(N3) in memory. This is only practical for small RNAs.
Results: I describe a divide and conquer variant of the alignment algorithm that is analogous to memory-efficient Myers/Miller dynamic programming algorithms for linear sequence alignment. The new algorithm has an O(N2 log N) memory complexity, at the expense of a small constant factor in time.
Conclusions: Optimal ribosomal RNA structural alignments that previously required up to 150 GB of memory now require less than 270 MB.
Figures
Figure 1
An example RNA sequence family. Top: a toy multiple alignment of three sequences, with 28 total columns, 24 of which will be modeled as consensus positions. The [structure] line annotates the consensus secondary structure: > and < symbols mark base pairs, x's mark consensus single stranded positions, and .'s mark "insert" columns that will not be considered part of the consensus model. Bottom: the secondary structure of the "human" sequence.
Figure 2
The structural alignment is converted to a guide tree. Left: the consensus secondary structure is derived from the annotated alignment in Figure 1. Numbers in the circles indicate alignment column coordinates: e.g. column 4 base pairs with column 14, and so on. Right: the CM guide tree corresponding to this consensus structure. The nodes of the tree are numbered 1..24 in preorder traversal (see text). MATP, MATL, and MATR nodes are associated with the columns they generate: e.g., node 6 is a MATP (pair) node that is associated with the base-paired columns 4 and 14.
Figure 3
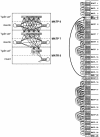
A complete covariance model. Right: the CM corresponding to the alignment in Figure 1. The model has 81 states (boxes, stacked in a vertical array). Each state is associated with one of the 24 nodes of the guide tree (text to the right of the state array). States corresponding to the consensus are in white. States responsible for insertions and deletions are gray. The transitions from bifurcation state B10 to start states S11 and S46 are in bold because they are special: they are an obligate (probability 1) bifurcation. All other transitions (thin arrows) are associated with transition probabilities. Emission probability distributions are not represented in the figure. Left: the states are also arranged according to the guide tree. A blow up of part of the model corresponding to nodes 6, 7, and 8 shows more clearly the logic of the connectivity of transition probabilities (see main text), and also shows why any parse tree must transit through one and only one state in each "split set".
Figure 4
Example parse trees. Parse trees are shown for the three sequences/structures from Figure 1, given the CM in Figure 3. For each sequence, each residue must be associated with a state in the parse tree. (The sequences can be read off its parse tree by starting at the upper left and reading counterclockwise around the edge of parse tree.) Each parse tree corresponds directly to a secondary structure – base pairs are pairs of residues aligned to MP states. A collection of parse trees also corresponds to a multiple alignment, by aligning residues that are associated with the same state – for example, all three trees have a residue aligned to state ML4, so these three residues would be aligned together. Insertions and deletions relative to the consensus use nonconsensus states, shown in gray.
Figure 5
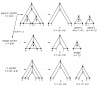
The three types of problems that need to be split. The sequence axis (e.g. x g..x q) is horizontal. The model subgraph axis for a contiguous set of states (e.g. states r..z) is vertical, where a solid lines means an unbifurcated model subgraph, and a dashed line means a model subgraph that may contain bifurcations. Closed circles indicate "inclusive of", and open circles indicate "exclusive of".
Figure 6
Empirical time and memory requirements for structural alignment. Plots of data from Table 1. Filled circles: divide and conquer algorithm; open circles: standard CYK algorithm. Left: Memory use in megabytes on a log-log scale. Lines represent weighted least-squares regression fits to the theoretically expected memory scaling: _aN_2 log N for divide and conquer (solid line) and aN_3 for standard CYK (dashed line). Right: CPU times in seconds on a log-log scale. Lines represent least-squares regression fits to a power law (aN_b). According to this fit, divide and conquer time (solid line) empirically scales as _N_3.24, and standard CYK without traceback (dashed line) scales as _N_3.29. A line representing O(_N_4) scaling (the theoretical upper bound on performance) is shown for comparison.
Similar articles
- Reduced space hidden Markov model training.
Tarnas C, Hughey R. Tarnas C, et al. Bioinformatics. 1998 Jun;14(5):401-6. doi: 10.1093/bioinformatics/14.5.401. Bioinformatics. 1998. PMID: 9682053 - Pair hidden Markov models on tree structures.
Sakakibara Y. Sakakibara Y. Bioinformatics. 2003;19 Suppl 1:i232-40. doi: 10.1093/bioinformatics/btg1032. Bioinformatics. 2003. PMID: 12855464 - Reduced space sequence alignment.
Grice JA, Hughey R, Speck D. Grice JA, et al. Comput Appl Biosci. 1997 Feb;13(1):45-53. doi: 10.1093/bioinformatics/13.1.45. Comput Appl Biosci. 1997. PMID: 9088708 - Energy-based RNA consensus secondary structure prediction in multiple sequence alignments.
Washietl S, Bernhart SH, Kellis M. Washietl S, et al. Methods Mol Biol. 2014;1097:125-41. doi: 10.1007/978-1-62703-709-9_7. Methods Mol Biol. 2014. PMID: 24639158 Review. - The art of editing RNA structural alignments.
Andersen ES. Andersen ES. Methods Mol Biol. 2014;1097:379-94. doi: 10.1007/978-1-62703-709-9_17. Methods Mol Biol. 2014. PMID: 24639168 Review.
Cited by
- Detecting and comparing non-coding RNAs in the high-throughput era.
Bussotti G, Notredame C, Enright AJ. Bussotti G, et al. Int J Mol Sci. 2013 Jul 24;14(8):15423-58. doi: 10.3390/ijms140815423. Int J Mol Sci. 2013. PMID: 23887659 Free PMC article. Review. - Genome-wide bioinformatic prediction and experimental evaluation of potential RNA thermometers.
Waldminghaus T, Gaubig LC, Narberhaus F. Waldminghaus T, et al. Mol Genet Genomics. 2007 Nov;278(5):555-64. doi: 10.1007/s00438-007-0272-7. Epub 2007 Jul 24. Mol Genet Genomics. 2007. PMID: 17647020 - RSEARCH: finding homologs of single structured RNA sequences.
Klein RJ, Eddy SR. Klein RJ, et al. BMC Bioinformatics. 2003 Sep 22;4:44. doi: 10.1186/1471-2105-4-44. BMC Bioinformatics. 2003. PMID: 14499004 Free PMC article. - Rfam: annotating non-coding RNAs in complete genomes.
Griffiths-Jones S, Moxon S, Marshall M, Khanna A, Eddy SR, Bateman A. Griffiths-Jones S, et al. Nucleic Acids Res. 2005 Jan 1;33(Database issue):D121-4. doi: 10.1093/nar/gki081. Nucleic Acids Res. 2005. PMID: 15608160 Free PMC article. - Fragrep: an efficient search tool for fragmented patterns in genomic sequences.
Mosig A, Sameith K, Stadler P. Mosig A, et al. Genomics Proteomics Bioinformatics. 2006 Feb;4(1):56-60. doi: 10.1016/S1672-0229(06)60017-X. Genomics Proteomics Bioinformatics. 2006. PMID: 16689703 Free PMC article.
References
- Eddy S. Computational genomics of noncoding RNA genes. Cell. 2002;109:137–140. - PubMed
- Laferriere A, Gautheret D, Cedergren R. An RNA pattern matching program with enhanced performance and portability. Comput. 1994;10:211–212. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous