Powerful regression-based quantitative-trait linkage analysis of general pedigrees - PubMed (original) (raw)

Powerful regression-based quantitative-trait linkage analysis of general pedigrees

Pak C Sham et al. Am J Hum Genet. 2002 Aug.

Abstract

We present a new method of quantitative-trait linkage analysis that combines the simplicity and robustness of regression-based methods and the generality and greater power of variance-components models. The new method is based on a regression of estimated identity-by-descent (IBD) sharing between relative pairs on the squared sums and squared differences of trait values of the relative pairs. The method is applicable to pedigrees of arbitrary structure and to pedigrees selected on the basis of trait value, provided that population parameters of the trait distribution can be correctly specified. Ambiguous IBD sharing (due to incomplete marker information) can be accommodated in the method by appropriate specification of the variance-covariance matrix of IBD sharing between relative pairs. We have implemented this regression-based method and have performed simulation studies to assess, under a range of conditions, estimation accuracy, type I error rate, and power. For normally distributed traits and in large samples, the method is found to give the correct type I error rate and an unbiased estimate of the proportion of trait variance accounted for by the additive effects of the locus-although, in cases where asymptotic theory is doubtful, significance levels should be checked by simulations. In large sibships, the new method is slightly more powerful than variance-components models. The proposed method provides a practical and powerful tool for the linkage analysis of quantitative traits.

PubMed Disclaimer

Figures

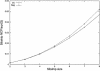
Figure 1

Figure 1

Theoretical sibship NCP over squared QTL variance

_Q_2

, obtained from equation (2) for the regression method and from appendix D for the VC method, under the assumption of a sibling correlation of 0.25.

Figure 2

Figure 2

Effect of model misspecification. Each point represents the average

χ2

statistic obtained from 2,000 simulated replicates, containing 250 sib quads. The QTL and residual polygenic variances are 0.2 and 0.3, respectively. In each case, the true trait model has mean 0, variance 1, and heritability 0.5. The misspecified mean, variance, and covariance are shown on the _X_-axes of panels a, b, and c, respectively. “Perfect marker” represents complete IBD information; “imperfect marker” represents a diallelic marker with equally frequent alleles.

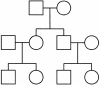
Figure 3

Figure 3

Structure for simulated cousin pedigree

Comment in

Similar articles

Cited by

References

Electronic-Database Information

    1. Genetic Power Calculator, http://statgen.iop.kcl.ac.uk/gpc/
    1. Merlin, http://www.sph.umich.edu/csg/abecasis/Merlin/

References

    1. Abecasis GR, Cherny SS, Cookson WO, Cardon LR (2002) Merlin—rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet 30:97–101 - PubMed
    1. Allison DB, Fernandez JR, Heo M, Beasley TM (2000) Testing the robustness of the new Haseman-Elston quantitative-trait loci-mapping procedure. Am J Hum Genet 67:249–252 - PMC - PubMed
    1. Almasy L, Blangero J (1998) Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet 62:1198–1211 - PMC - PubMed
    1. Amos CI (1994) Robust variance-components approach for assessing genetic linkage in pedigrees. Am J Hum Genet 54:535–543 - PMC - PubMed
    1. Blackwelder WC, Elston RC (1985) A comparison of sib-pair linkage tests for disease susceptibility loci. Genet Epidemiol 2:85–97 - PubMed

Publication types

MeSH terms

LinkOut - more resources