Metapopulation dynamics and spatial heterogeneity in cancer - PubMed (original) (raw)

Metapopulation dynamics and spatial heterogeneity in cancer

Isabel González-García et al. Proc Natl Acad Sci U S A. 2002.

Abstract

With the advent of drugs targeting specific molecular defects in cancerous cells [Gorre, M. E., et al. (2001) Science 293, 876-880], it is important to understand the degree of genetic heterogeneity present in tumor cell populations and the rules that govern microdiversity in human cancer. Here, we first show that populations with different genotypes in genes influencing cell growth and programmed cell death coexist in advanced malignant tumors of the colon, exhibiting microsatellite instability. Detailed, physical mapping of the diverse populations shows them to be arranged in small, intermingling areas, resulting in a variegated pattern of diversity. Using computational modeling of the experimental data, we find that the coexistence between similar competitors is enhanced, instead of deterred, by spatial dynamics [Hanski, I. (1999) Metapopulation Dynamics (Oxford Univ. Press, New York)]. The model suggests a simple and plausible scenario for the generation of spatial heterogeneity during tumor progression. The emergence and persistence of the patterns of diversity encountered in the tumors can be generated without a need to invoke differences in mutation rates, neutrality of interactions, or separated time scales. We posit that the rules that apply to spatial ecology and explain the maintenance of diversity are also at work in tumors and may underlie tumor microheterogeneity.

PubMed Disclaimer

Figures

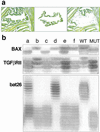
Figure 1

Figure 1

(a) The micrographs show how a tumoral glandular structure is acquired: from the field (Left), a single structure is lifted from the tissue (Center). The result (Right) verifies the purity of the microdissected cell population. Each pool of cells analyzed represents the population of tumor cells enclosed in a contiguous surface of 100 μm2. (b) The results of the genetic analysis can be interpreted easily for each of the selected areas. Lane e shows a BAX+/−; TGFβRII+/−; bat26−/−. Heterozygosity is not caused by contamination of normal cell elements because the DNA extracted from a single area often shows a mut/mut genotype for one of the three loci examined. The 27 possible genotypes for any given area make it unlikely that heterozygosity would be caused by an equal mixture of +/+ and −/− cells.

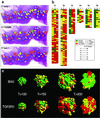
Figure 2

Figure 2

(a) The dappled pattern of heterogeneity is shown for one of the tumors studied. Note the diversity of genotypes generated when three loci are referred to a single area. The micrograph of the tumor also illustrates the advanced stage of the tumor growth, which penetrates the entire thickness of the intestinal wall. (b) Summary of results for the six tumors studied. Each gene is represented in a column, with each file through the three columns representing an independently sampled area of the tumor. In many instances, an area that contains cells with two mutated alleles (e.g., TGFβRII and bat26) and a WT BAX can be seen. Tumors are arranged from the most cellular to the least cellular because of large mucin pools. The mucinous tumors, although in the same size category, yielded less cellular areas for genotypic characterization. (c) The geographical distribution of clones in the model indicates that the parameters found by the algorithm are close to the experimental data. The optional parameters found by the search algorithm were: δ = 0.01, μ = 0.0021, _D_1 = 0.760, _D_2 = 0.376, _R_1 = 1.399, _R_2 = 1.413. A cross-section of the 3D representation generated by the model shows the intermingling of clones with diverse genotypes to be close to the experimental findings.

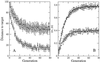
Figure 3

Figure 3

The robustness of the search algorithm is shown. (A) The average distance (●) and the distance to the target for the optimal solution (○) is shown (the SDs are obtained over 10 different runs of the search algorithm). After ≈40 generations, near-optimal solutions already are obtained. (B) An example of the optimal values obtained for the parameters controlling apoptosis: _D_1 (■) and _D_2 (□) (see model description). The SD is shown (under the same conditions as in A). The curves show that different runs of the search algorithm reach basically the same parameter values.

Similar articles

Cited by

References

    1. Nowell P C. Science. 1976;194:23–28. - PubMed
    1. Waghorne C, Thomas M, Lagarde A, Kerbel R S, Breitman M-L. Cancer Res. 1988;48:6109–6114. - PubMed
    1. Fearon E-R, Vogelstein B. Cell. 1990;61:759–767. - PubMed
    1. Cavenee W-K, Scrable H-J, James C-D. Mutat Res. 1991;247:199–202. - PubMed
    1. Boland C-R, Sato J, Appelman H-D, Bresalier R-S, Feinberg A-P. Nat Med. 1995;1:902–909. - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources