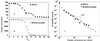Expanding protein universe and its origin from the biological Big Bang - PubMed (original) (raw)

Expanding protein universe and its origin from the biological Big Bang

Nikolay V Dokholyan et al. Proc Natl Acad Sci U S A. 2002.

Abstract

The bottom-up approach to understanding the evolution of organisms is by studying molecular evolution. With the large number of protein structures identified in the past decades, we have discovered peculiar patterns that nature imprints on protein structural space in the course of evolution. In particular, we have discovered that the universe of protein structures is organized hierarchically into a scale-free network. By understanding the cause of these patterns, we attempt to glance at the very origin of life.

PubMed Disclaimer

Figures

Fig 1.

Fig 1.

An example of a large cluster of TIM barrel-fold protein domains. Protein domains whose DALI similarity Z score is greater than Zmin = 9 are connected by lines.

Fig 2.

Fig 2.

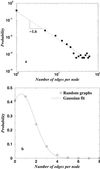
The dependence of the number of proteins in the maximal cluster on the threshold value of Z score Zmin for PDUG (a) and random graphs (b). (c) The probability density of the cluster sizes for PDUG and random graphs at their respective Zc. Zc indicates the critical value of the Z score threshold at which transition in the size of maximal cluster occurs. For PDUG Zc ≈ 9; for random graphs Zc ≈ 11. We generated 10 different realizations of random graphs, so each point of b represents an average over these 10 realizations. Interestingly, at minimal Zmin = 2, all of the nodes in random graphs are connected; thus, the largest cluster spans all of the protein domains. In contrast, just a small fraction of all nodes (≈250) constitutes the largest cluster in PDUG (at Zmin = 2), pointing to a dramatic difference between PDUG and random graphs. This difference is further revealed in Fig. 3.

Fig 3.

Fig 3.

The distribution of node connectivity 𝒫(k) for PDUG (a) and for random graph (b) at their corresponding Zc. For PDUG Zc ≈ 9; for random graphs Zc ≈ 11. Node connectivity denotes how many proteins a given protein is connected to by structural similarity connections.

Fig 4.

Fig 4.

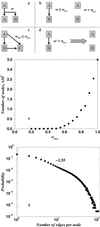
Proposed model of domain evolution. (a) Gene duplication (A → A + B): the structural similarity between A and B is defined by some function w = (A,B) (e.g., RMSD or DRMSD). (b) If structural similarity w = (A,B) is greater than some critical value w max, then we add a link connecting A and B. If structural similarity is above w max, a new fold family is born. (c) The second generation progeny C (A → B → C) can connect to its grandparent A, if there is structural similarity between A and C: w AC ≤ w max. (d) With each time step, mutations diverge protein structures from each other; i.e., structural similarity changes by some value D: w → _w_′ = w + D(D = 10−4). If _w_′ > w max, we remove the edge between corresponding proteins. (e) The dependence of the size of the largest cluster in the graphs generated by our model on wmax, averaged over 20 realizations. (f) The probability of the node connectivity in our model, averaged over 102 realizations. Apart from the finite-size effects at large k, it exhibits power law distribution with exponent α ≈ 1.6.

Similar articles

Cited by

References

    1. Rost B. (1997) Folding Des. 2, S19-S24. - PubMed
    1. Holm L. & Sander, C. (1993) J. Mol. Biol. 233, 123-138. - PubMed
    1. Holm L. & Sander, C. (1997) Proteins 28, 72-82. - PubMed
    1. Dokholyan N. V. & Shakhnovich, E. I. (2001) J. Mol. Biol. 312, 289-307. - PubMed
    1. Shakhnovich E. I. (1998) Folding Des. 3, R45-R58. - PubMed

Publication types

MeSH terms

Substances

Grants and funding

LinkOut - more resources