Discrete models of autocrine cell communication in epithelial layers - PubMed (original) (raw)

Comparative Study

Discrete models of autocrine cell communication in epithelial layers

Michal Pribyl et al. Biophys J. 2003 Jun.

Abstract

Pattern formation in epithelial layers heavily relies on cell communication by secreted ligands. Whereas the experimentally observed signaling patterns can be visualized at single-cell resolution, a biophysical framework for their interpretation is currently lacking. To this end, we develop a family of discrete models of cell communication in epithelial layers. The models are based on the introduction of cell-to-cell coupling coefficients that characterize the spatial range of intercellular signaling by diffusing ligands. We derive the coupling coefficients as functions of geometric, cellular, and molecular parameters of the ligand transport problem. Using these coupling coefficients, we analyze a nonlinear model of positive feedback between ligand release and binding. In particular, we study criteria of existence of the patterns consisting of clusters of a few signaling cells, as well as the onset of signal propagation. We use our model to interpret recent experimental studies of the EGFR/Rhomboid/Spitz module in Drosophila development.

PubMed Disclaimer

Figures

FIGURE 1

FIGURE 1

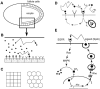
(A) The geometry of the problem is motivated by cell communication in Drosophila oogenesis. Epithelial cells cover the large oocyte. EGF receptors are uniformly distributed across the epithelial layer and are absent on the surface of the oocyte. (B) Ligands diffuse in a thin gap between the epithelial layer and a reflective surface. (C) The two model layers considered in this article—periodic arrays of squares and hexagons. (D) Main processes in ligand binding and transport. (E) Ligand binding stimulates ligand release. Receptor activation leads to the degradation of a factor inhibiting the transcription of the ligand-releasing protease. In the absence of inhibition, the protease is synthesized and generates the secreted ligand.

FIGURE 2

FIGURE 2

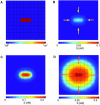
The steady-state ligand field due to a single ligand-releasing cell. (A) Square cells, _L_x = 5 × 10−4 cm. (B) Hexagonal cells, 2_L_v = 5 × 10−4 cm. Other parameters: h = 5 × 10−5 cm, _k_e = 0.1 min−1, _k_off = 0.1 min−1, _R_0 = 1 × 104 molecules/cell surface, D = 1 × 10−7 cm2 s−1, _k_on = 0.1 nM−1 min−1, and _Q_s = 100 molecules/cell/min. The fields were computed by solving Eq. 12 using an adaptive mesh finite element package (FEMLAB).

FIGURE 3

FIGURE 3

Normalized coupling coefficients (formula image, see text for details) plotted as a function of cell-to-cell distance, k, defined as the ratio of the Euclidian distance divided by the cell size. (A) Effect of ligand-receptor affinity _k_on (square cells, _L_x = 5 × 10−4 cm, D = 1 × 10−7 cm2 s−1). (B) Effect of ligand diffusivity D (hexagonal cells, 2_L_v = 5 × 10−4 cm; _k_on = 0.1 nM−1 min−1). All other parameters are as in Fig. 2.

FIGURE 4

FIGURE 4

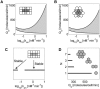
Stable localized patterns generated by the positive feedback. Existence of the localized three-cell patterns for squares (A) and hexagons (B) as a function of ligand release rate and ligand-receptor affinity. The shaded area corresponds to the stable localized pattern. Crossing the upper boundary ignites the neighboring cells. Crossing the lower boundary leads to the extinction of the pattern. (C) A one-dimensional cut (_Q_s = 300 molecules/cell/min) through the diagram in A showing the disconnected region of existence of the localized pattern. Localized patterns are realized both for low and high ligand-receptor affinities. (D) Critical rate of ligand release necessary to destabilize the localized pattern as a function of the number of cells in it, _k_on = 0.1 nM−1 min−1. A_–_D: _C_T = 500 molecules/cell. Other parameters are as in Fig. 2.

FIGURE 5

FIGURE 5

Response of a cellular layer to a localized perturbation in protease release. (A) The structure of the perturbation. B_–_D, The ligand fields induced by the perturbation computed for different ligand-release rates. (B) _Q_s = 100 molecules/cell/min. Ligand field 40 min after the perturbation. The perturbation decays. (C) _Q_s = 200 molecules/cell/min. The perturbation generates a stable pattern of the same structure. (D) _Q_s = 300 molecules/cell/min. The perturbation generates an “ignition” wave (see text for details). All parameters are as in Fig. 4 A.

FIGURE 6

FIGURE 6

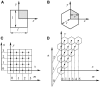
(A) Solution of Eq. 12 for the square cells was derived on the two-dimensional semi-infinite domain with the origin in the center of the square. The dimensionless area of the square is formula image. (B) Solution of Eq. 12 for the hexagons was derived on the two-dimensional, semi-infinite domain with origin in the center of the hexagon. The dimensionless area of the hexagon is a = 3 × r × v. (C) Indexing used for the computation of coupling coefficients for square cells. (D) Indexing used for the computation of coupling coefficients for hexagonal cells.

Similar articles

Cited by

References

    1. Amiri, A., and D. Stein. 2002. Dorsoventral patterning: a direct route from ovary to embryo. Curr. Biol. 12:R532–R534. - PubMed
    1. Bergmann, A., M. Tugentman, B. Shilo, and H. Steller. 2002. Regulation of cell number by MAPK-dependent control of apoptosis. a mechanism for trophic survival signaling. Dev. Cell. 2:159–170. - PubMed
    1. Bolouri, H., and E. H. Davidson. 2002. Modeling transcriptional regulatory networks. Bioessays. 24:1118–1129. - PubMed
    1. Brand, A. H., and N. Perrimon. 1993. Targeted gene expression as a means of altering cell fates and generating dominant phenotypes. Development. 118:401–415. - PubMed
    1. Cahn, J. W., J. Mallet-Paret, and E. S. Van Vleck. 1998. Traveling wave solutions for systems of ODEs on a two-dimensional spatial lattice. SIAM J. Appl. Math. 59:455–493.

Publication types

MeSH terms

Substances

LinkOut - more resources