Factors that make an infectious disease outbreak controllable - PubMed (original) (raw)

Factors that make an infectious disease outbreak controllable

Christophe Fraser et al. Proc Natl Acad Sci U S A. 2004.

Abstract

The aim of this study is to identify general properties of emerging infectious agents that determine the likely success of two simple public health measures in controlling outbreaks, namely (i) isolating symptomatic individuals and (ii) tracing and quarantining their contacts. Because these measures depend on the recognition of specific disease symptoms, we investigate the relative timing of infectiousness and the appearance of symptoms by using a mathematical model. We show that the success of these control measures is determined as much by the proportion of transmission occurring prior to the onset of overt clinical symptoms (or via asymptomatic infection) as the inherent transmissibility of the etiological agent (measured by the reproductive number R(0)). From published studies, we estimate these quantities for two moderately transmissible viruses, severe acute respiratory syndrome coronavirus and HIV, and for two highly transmissible viruses, smallpox and pandemic influenza. We conclude that severe acute respiratory syndrome and smallpox are easier to control using these simple public health measures. Direct estimation of the proportion of asymptomatic and presymptomatic infections is achievable by contact tracing and should be a priority during an outbreak of a novel infectious agent.

PubMed Disclaimer

Figures

Fig. 1.

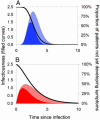
Fig. 1.

Key epidemiological determinants. These determinants describe the pattern of typical disease progression for an individual patient as a function of time since infection (measured in arbitrary units). Filled curves represent infectiousness through time (left axis). The black curve represents S(τ), the probability of a person not having developed symptoms by a certain time (right axis). The basic reproduction number _R_0 is the area under the infectiousness curve (solid color plus cross-hatched section). The solid-colored area represents transmission arising prior to symptoms such that θ, the proportion of presymptomatic transmission, is the proportion of the total area under the infectiousness curve that is solid-colored. (A and B) Low- and high-variance incubation and infectiousness distributions, respectively. Both cases have _R_0 = 5, _T_g = 3 (in arbitrary time units), andθ = 0.5; A shows a low variance of 0.1 × mean2, whereas B shows a high variance of 0.5 × mean2.

Fig. 2.

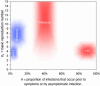
Fig. 2.

Parameter estimates. Plausible ranges for the key parameters _R_0 and θ (see main text for sources) for four viral infections of public concern are shown as shaded regions. The size of the shaded area reflects the uncertainties in the parameter estimates. The areas are color-coded to match the assumed variance values for β(τ) and S(τ) of Fig. 1 appropriate for each disease, for reasons that are apparent in Fig. 3.

Fig. 3.

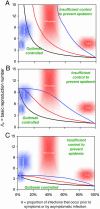
Fig. 3.

Criteria for outbreak control. Each curve represents a different scenario, consisting of a combination of interventions and a choice of parameters. For each scenario, if a given infectious agent is below the _R_0–θ curve, the outbreak is always controlled eventually. Above the curve, additional control measures (e.g., movement restrictions) would be required to control spread. Black lines correspond to isolating symptomatic individuals only. Colored lines correspond to the addition of immediate tracing and quarantining of all contacts of isolated symptomatic individuals. The black (isolation only) line is independent of distributional assumptions made (low or high variance), whereas the colored (isolation + contact tracing) lines match the variance assumptions made in Fig. 1 (red = high variance; blue = low variance). The efficacy of isolation of symptomatic individuals is 100% in A, 90% in B, and 75% in C. Contact tracing and isolation is always assumed 100% effective in the scenarios in which it is implemented (colored lines). Curves are calculated by using a mathematical model of outbreak spread incorporating quarantining and contact tracing (see main text).

Similar articles

Cited by

References

    1. Pearson, H., Clarke, T., Abbott, A., Knight, J. & Cyranoski, D. (2003) Nature 424, 121-126. - PMC - PubMed
    1. Riley, S., Fraser, C., Donnelly, C. A., Ghani, A. C., Abu-Raddad, L. J., Hedley, A. J., Leung, G. M., Ho, L. M., Lam, T. H., Thach, T. Q., et al. (2003) Science 300, 1961-1966. - PubMed
    1. Lipsitch, M., Cohen, T., Cooper, B., Robins, J. M., Ma, S., James, L., Gopalakrishna, G., Chew, S. K., Tan, C. C., Samore, M. H., et al. (2003) Science 300, 1966-1970. - PMC - PubMed
    1. Donnelly, C. A., Ghani, A. C., Leung, G. M., Hedley, A. J., Fraser, C., Riley, S., Abu-Raddad, L. J., Ho, L. M., Thach, T. Q., Chau, P., et al. (2003) Lancet 361, 1761-1766. - PMC - PubMed
    1. Peiris, J. S., Chu, C. M., Cheng, V. C., Chan, K. S., Hung, I. F., Poor, L. L., Law, K. I., Tang, B. S., Hon, T. Y., Chan, C. S., et al. (2003) Lancet 361, 1767-1772. - PMC - PubMed

MeSH terms

LinkOut - more resources