Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond - PubMed (original) (raw)
Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond
Evan Evans et al. Proc Natl Acad Sci U S A. 2004.
Abstract
Many biomolecular bonds exhibit a mechanical strength that increases in proportion to the logarithm of the rate of force application. Consistent with exponential decrease in bond lifetime under rising force, this kinetically limited failure reflects dissociation along a single thermodynamic pathway impeded by a sharp free energy barrier. Using a sensitive force probe to test the leukocyte adhesion bond P-selectin glycoprotein ligand 1 (PSGL-1)-P-selectin, we observed a linear increase of bond strength with each 10-fold increase in the rate of force application from 300 to 30,000 pN/sec, implying a single pathway for failure. However, the strength and lifetime of PSGL-1-P-selectin bonds dropped anomalously when loaded below 300 pN/sec, demonstrating unexpectedly faster dissociation and a possible second pathway for failure. Remarkably, if first loaded by a "jump" in force to 20-30 pN, the bonds became strong when subjected to a force ramp as slow as 30 pN/sec and exhibited the same single-pathway kinetics under all force rates. Applied in this way, a new "jump/ramp" mode of force spectroscopy was used to show that the PSGL-1-P-selectin bond behaves as a mechanochemical switch where force history selects between two dissociation pathways with markedly different properties. Furthermore, replacing PSGL-1 by variants of its 19-aa N terminus and by the crucial tetrasaccharide sialyl LewisX produces dramatic changes in the failure kinetics, suggesting a structural basis for the two pathways. The two-pathway switch seems to provide a mechanism for the "catch bond" response observed recently with PSGL-1-P-selectin bonds subjected to small-constant forces.
Figures
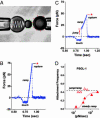
Fig. 1.
Videomicrograph (A) of the BFP (labeled by the “spring” on the left) juxtaposed with a 4-μm target microsphere; force-time plot (B) from a steady ramp test of a P-selectin–PSGL-1 bond; force time plot (C) from a jump/ramp test of a P-selectin–PSGL-1 bond; comparison of the perceived frequencies (D) of BFP tip-target attachments in jump/ramp and steady ramp tests of P-selectin–PSGL-1 bonds. (A) Pressurized by pipette suction, a PEG-biotinylated red blood cell acts as the elastic transducer for force in the BFP. To form an active tip, a 2-μm glass bead was bound with P-selectin (“green pins”) as well as PEG biotin and then attached to the transducer with streptavidin. With the PSGL-1 ligands (“red wedges”) linked covalently to a target glass bead (on the right) in the same way, bonds to P-selectin were formed and broken by moving the target into and out of contact with the BFP tip by using a piezo-mounted pipette. (B) A steady ramp test shows the BFP response during target approach “soft” touch, then retraction at fixed speed. Formed at touch, a PSGL-1–P-selectin bond failed at ≈75 pN under the force ramp of ≈700 pN/sec. (C) A jump/ramp test shows the BFP response during target approach, touch, then a rapid retraction abruptly switched after 0.004 sec to slow retraction. Again formed at touch and surviving the jump in force (at ≈5,000 pN/sec), a PSGL-1–P-selectin bond failed at ≈50 pN under the final force ramp of ≈140 pN/sec. (D) Frequencies of tip-surface attachments in steady ramp tests appeared to increase with ramp rate (filled red triangles), whereas frequencies in the jump/ramp tests were essentially independent of ramp rate (open red triangles). The dotted red curve estimates the apparent frequency that would be perceived if some attachments went undetected under steady ramps within the first force bin (≈10–12 pN), assuming rapid dissociation (≈10 pN/sec) along a separate pathway that could be blocked by a 20- to 30-pN jump in force.
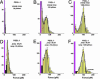
Fig. 2.
Force histograms for PSGL-1–P-selectin bonds ruptured under steady ramps (A_–_C) and under jump/ramps (D_–_F). Forces in the first bin include tests without detection of an attachment, which causes the first bin (magenta) to rise off-scale. As shown by a 40–45% attachment frequency for D_–_F in contrast to <10% for A, ≈25% for B, and ≈33% for C, the quick initital jumps in force to ≈20–30 pN captured numerous bonds otherwise missed because of fast failure along a low-impedance pathway within the time increment defined by the first bin (see Fig. 1_D_). (The few bonds that broke during the jump phase are shown by the dark bins in D_–_F.) After force jumps or under fast steady ramps, the force distributions are seen to agree with the probability densities (dashed red curves) predicted for kinetically limited failure along a single pathway (labeled 2) defined by the failure rate, _k_2rup ≈ (0.37 ± 0.07pN/sec) exp(f/18 ± 0.5 pN). Superimposed as solid black curves are the probability distributions computed by using the master equation for the two-pathway switch described in the text. To match the histograms for both steady ramp and jump/ramp modes at all loading rates, the two-pathway dissociation was modeled by a fast rate of _k_1rup ≈ 8–12 pN/sec along low-impedance pathway 1 and a switch to high-impedance pathway 2 in the range of ≈20–25 pN. [It appears that a few (<20% in all cases) double bonds led to the small tails of very high forces, as shown by the predicted distribution added to the histogram in F.]
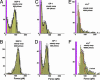
Fig. 4.
Force histograms obtained from steady ramp tests of SGP-3–P-selectin bonds (A and B), GP-1–P-selectin bonds (C and D), and b-sLeX–P-selectin bonds (E and F). Superposed in A_–_D are the probability distributions computed for the two-pathway switch (solid dark curves) as well as the kinetically limited pathway distributions (dashed red curves). (A and B) Match of the two-pathway model to the data for SGP-3–P-selectin bonds gave parameters similar to those obtained for PSGL-1–P-selectin bonds (see Fig. 6): i.e., a rate of _k_1rup ≈ 7–13/sec for dissociation along the first pathway and switch to the second pathway above ≈20–30 pN defined by the failure rate, _k_2rup ≈ (0.2 ± 0.1/sec) exp(f/16 ± 0.5 pN). (C and D) Optimal match to the data for GP-1–P-selectin bonds yielded a rate of _k_1rup ≈ 50 ± 10/sec along pathway 1, followed by a switch to pathway 2 above ≈20 pN defined by the rate _k_2rup ≈ (0.3 ± 0.1/sec) exp(f/14 ± 0.5 pN). (E and F) Superimposed (dotted red curve) on the data for b-sLeX–P-selectin bonds are probability densities for a single kinetically limited pathway defined by the failure rate _k_rup ≈ (90 ± 10/sec) exp(f/20 ± 1 pN). Also shown in E is the broadening (dotted blue curve) expected from error (σexp ≈± 10–11 pN) in force detection with the large BFP stiffness needed for ultrafast loading. Similarly, a gap appears between the magenta bin and the lowest forces detected because of the limitation by video framing rate (≈1,500/sec) at very fast pulling speeds. [Again, a few (<20% in all cases) double bonds seem to account for the tails of very high forces, as shown by the predicted distribution added to the histogram in F.]
Fig. 3.
The most frequent forces (highest peaks in histograms) obtained from steady ramp and jump/ramp tests of PSGL-1–P-selectin bonds are plotted as functions of log10(ramp rate). Conceptual energy landscape for a two-pathway switch. In A, the solid green wedges and solid red triangles are the force positions for the highest peaks under steady ramps (see Fig. 2 A_–_C), which show an abrupt change in the expected value of bond strength (from solid green wedges to solid red triangles) near 300 pN/sec. The open red triangles are force positions for the single peaks found in histograms under steady ramps after jumps to ≈20–30 pN. Continuing the linear proportionality down to ≈35 pN/sec, the most frequent rupture forces in jump/ramp tests overlap precisely with the solid red triangles at loading rates >300 pN/sec. Consistent with the dynamical transition in bond strength under steady ramp loading, jumps to ≈20–30 pN in <0.01 sec blocked access to the initial low-impedence pathway, allowing failure only along the high-impedance pathway. In our model of the two-pathway switch, the initial pathway is closed off when the occupancy ratio of the two bound configurations is quickly inverted. (B) Conceptual energy contours along two pathways in configuration space originating from separate bound states that couple in different ways to the pulling force, as modeled by the single master equation in the text. The energy contour along pathway 1 is viewed as essentially orthogonal to the pulling direction, so that force has little effect on failure rate. In contrast, the energy contour along pathway 2 is aligned significantly with the pulling direction (but need not be coparallel). Key to the switching mechanism, the small difference in energy levels between the two bound states is shifted by the force from favoring pathway 1 to pathway 2.
Fig. 5.
The mean lifetimes of PSGL-1–P-selectin, GP-1–P-selectin, and b-sLeX–P-selectin bonds plotted as continuous functions of force (A) and correlation of the two-pathway model to the mean lifetimes measured for neutrophil and PSGL-1 bead tethers to P-selectin in a flow chamber under different shear rates (data from ref. 8) (B). (A) Needed to match histograms under steady ramp and jump/ramp force histories (see legend of Fig. 2 for PSGL-1–P-selectin and legend of Fig. 4 for GP-1–P-selectin and b-sLeX–P-selectin), the mean rates of failure are continuous functions of applied force, the reciprocals being equivalent to the mean lifetimes expected at constant force. The red dashed line defines the lifetime if restricted to dissociation along the high-impedance pathway for PSGL-1–P-selectin. (B) Using the force scale _f_β = 18 pN for rate exponentiation along pathway 2, the two-pathway model was fit to the data from ref. , assuming that the cell and bead attachments in the flow chamber experiments were held by an average of two bonds. The solid black curve shows the lifetime for one bond predicted by the two-pathway parameters: _k_1rup ≈ 7/sec, _k_2rup = (0.45/sec) exp(f/18 pN), and a crossover in force at ≈15–20 pN. The dashed black curve shows the lifetime 〈_t_〉 expected for two of these bonds that equally share the force f and fail randomly; i.e., 〈_t_〉= [_k_rup(f) + 2 _k_rup(f/2)]/[2 _k_rup(f) _k_rup(f/2)], where _k_rup(f) defines the failure rate for one bond.
Similar articles
- Chemically distinct transition states govern rapid dissociation of single L-selectin bonds under force.
Evans E, Leung A, Hammer D, Simon S. Evans E, et al. Proc Natl Acad Sci U S A. 2001 Mar 27;98(7):3784-9. doi: 10.1073/pnas.061324998. Epub 2001 Mar 13. Proc Natl Acad Sci U S A. 2001. PMID: 11274395 Free PMC article. - Theoretical aspects of the biological catch bond.
Prezhdo OV, Pereverzev YV. Prezhdo OV, et al. Acc Chem Res. 2009 Jun 16;42(6):693-703. doi: 10.1021/ar800202z. Acc Chem Res. 2009. PMID: 19331389 Review. - Regulation of catch bonds by rate of force application.
Sarangapani KK, Qian J, Chen W, Zarnitsyna VI, Mehta P, Yago T, McEver RP, Zhu C. Sarangapani KK, et al. J Biol Chem. 2011 Sep 16;286(37):32749-61. doi: 10.1074/jbc.M111.240044. Epub 2011 Jul 20. J Biol Chem. 2011. PMID: 21775439 Free PMC article. - Nano-to-micro scale dynamics of P-selectin detachment from leukocyte interfaces. III. Numerical simulation of tethering under flow.
King MR, Heinrich V, Evans E, Hammer DA. King MR, et al. Biophys J. 2005 Mar;88(3):1676-83. doi: 10.1529/biophysj.104.051805. Epub 2004 Dec 1. Biophys J. 2005. PMID: 15574709 Free PMC article. - For catch bonds, it all hinges on the interdomain region.
Thomas W. Thomas W. J Cell Biol. 2006 Sep 25;174(7):911-3. doi: 10.1083/jcb.200609029. J Cell Biol. 2006. PMID: 17000873 Free PMC article. Review.
Cited by
- Rupture of single receptor-ligand bonds: a new insight into probability distribution function.
Gupta VK. Gupta VK. Colloids Surf B Biointerfaces. 2013 Jan 1;101:501-9. doi: 10.1016/j.colsurfb.2012.07.020. Epub 2012 Jul 27. Colloids Surf B Biointerfaces. 2013. PMID: 23010061 Free PMC article. - The Application of Micropipette Aspiration in Molecular Mechanics of Single Cells.
Lee LM, Liu AP. Lee LM, et al. J Nanotechnol Eng Med. 2014 Nov;5(4):0408011-408016. doi: 10.1115/1.4029936. J Nanotechnol Eng Med. 2014. PMID: 26155329 Free PMC article. Review. - A model for cyclic mechanical reinforcement.
Li Z, Kong F, Zhu C. Li Z, et al. Sci Rep. 2016 Oct 27;6:35954. doi: 10.1038/srep35954. Sci Rep. 2016. PMID: 27786286 Free PMC article. - Molecular mechanisms of catch bonds and their implications for platelet hemostasis.
Belyaev AV, Fedotova IV. Belyaev AV, et al. Biophys Rev. 2023 Sep 26;15(5):1233-1256. doi: 10.1007/s12551-023-01144-8. eCollection 2023 Oct. Biophys Rev. 2023. PMID: 37974999 Free PMC article. Review. - The effect of different force applications on the protein-protein complex Barnase-Barstar.
Neumann J, Gottschalk KE. Neumann J, et al. Biophys J. 2009 Sep 16;97(6):1687-99. doi: 10.1016/j.bpj.2009.01.052. Biophys J. 2009. PMID: 19751674 Free PMC article.
References
- McEver, R. P. (2001) Thromb. Haemostasis 86, 746–756. - PubMed
- McEver, R. P. (2002) Curr. Opin. Cell Biol. 14, 581–586. - PubMed
- Alon, R., Hammer, D. A. & Springer, T. A. (1995) Nature 374, 539–542. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
- R01 AI044902/AI/NIAID NIH HHS/United States
- R01 HL031579/HL/NHLBI NIH HHS/United States
- R01 HL065333/HL/NHLBI NIH HHS/United States
- HL65333/HL/NHLBI NIH HHS/United States
- R21 AI044902/AI/NIAID NIH HHS/United States
- AI44902/AI/NIAID NIH HHS/United States
- HL31579/HL/NHLBI NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources