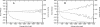Indel-based evolutionary distance and mouse-human divergence - PubMed (original) (raw)
Comparative Study
Indel-based evolutionary distance and mouse-human divergence
Aleksey Y Ogurtsov et al. Genome Res. 2004 Aug.
Abstract
We propose a method for estimating the evolutionary distance between DNA sequences in terms of insertions and deletions (indels), defined as the per site number of indels accumulated in the course of divergence of the two sequences. We derive a maximal likelihood estimate of this distance from differences between lengths of orthologous introns or other segments of sequences delimited by conservative markers. When indels accumulate, lengths of orthologous introns diverge only slightly slower than linearly, because long indels occur with substantial frequencies. Thus, saturation is not a major obstacle for estimating indel-based evolutionary distance. For introns of medium lengths, our method recovers the known evolutionary distance between rat and mouse, 0.014 indels per site, with good precision. We estimate that mouse-human divergence exceeds rat-mouse divergence by a factor of 4, so that mouse-human evolutionary distance in terms of selectively neutral indels is 0.056. Because in mammals, indels are approximately 14 times less frequent than nucleotide substitutions, mouse-human evolutionary distance in terms of selectively neutral substitutions is approximately 0.8.
Copyright 2004 Cold Spring Harbor Laboratory Press ISSN
Figures
Figure 1
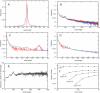
Lengths of individual indels. pm(δ) and ph(δ), distributions of lengths of all indels in all alignments (A) of rat–mouse (blue line) and human–OWM (red line) intron pairs. p+(δ) and p_–(–δ), distributions of the absolute value of length of indels of only positive lengths (red line) and only negative lengths (blue line) in all rat–mouse alignments (B). P(δ) = (p+(δ)_ + p_–(–δ)_)/2, the averaged distribution of the absolute value of length of indels with positive and negative lengths in all rat–mouse (blue line) and human–OWM (red line) alignments (C). The same as the previous figure, but indels were recorded only in those parts of alignments where neither of the two sequences was masked by RepeatMasker (D). P(δ) in all rat–mouse alignments, multiplied by δ2(E). Properties of distributions P(δ) obtained for rat–mouse pairs of introns with the following average lengths: 0–100, 100–200, 200–400,..., 6400–12800. For each distribution, fractions of indels of length 1 and of indels longer than 100, 300, and 1000 nucleotides are shown (F).
Figure 2
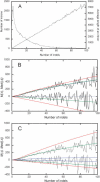
Data on rat–mouse pairs of orthologous introns with different numbers of accumulated indels, k. Numbers and average length L of intron pairs (A). Data on M(Δ) (decreasing lines) and Med(|Δ|) (increasing lines) in all intron alignments (rugged lines) compared with theoretical predictions (equation 1; smooth lines) obtained with a = 0.5 (blue lines), 0.46 (green lines), and 0.38 (red lines) under P(δ) (equation 7) for intron pairs with the average lengths between 150 and 2500 (B), or with P(δ) for intron pairs of average lengths >150 (blue lines), between 150 and 2500 (green lines), and <2500 (red lines) under a = 0.46 (C).
Figure 3
Properties of intron pairs as functions of their average length, L. Numbers of introns with different values of L (in bins of size 50), and the corresponding M(Δ) (decreasing lines) and Med(|Δ|) (increasing lines) are shown for rat–mouse (A) and mouse–human (B) intron pairs.
Figure 4
The relationship between M(Δ) and Med(|Δ|) in intron pairs with different L (as in Fig. 3) in rat–mouse (A) and mouse–human (B) intron pairs, compared with theoretical predictions (equation 1), obtained under P(δ) calculated for intron pairs of with 150 < L < 2500 and several values of a.
Figure 5
Indel-based evolutionary distance q for intron pairs of different average lengths L (in bins of size 100, data points are shown at the top boundaries of bins; for each bin, its own P(δ) was used). For rat and mouse, actual data (red line) and the maximal likelihood estimate of q (black line, a = 0.46) are shown. For mouse and human, estimates of q under a = 0.46, 0.42, and 0.38 are shown. The blue line shows the ratio of mouse–human over rat–mouse estimates of q. The green line shows the same ratio, computed for only those parts of mouse and human intron sequences that are not masked by RepeatMasker, on the basis of P(δ), calculated from repeat-free parts of rat–mouse alignments.
Figure 6
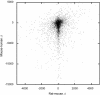
Length differences between rat and mouse introns, and between mouse and human introns that belong to the same rat–mouse–human triplet of orthologous introns.
Similar articles
- Indel evolution of mammalian introns and the utility of non-coding nuclear markers in eutherian phylogenetics.
Matthee CA, Eick G, Willows-Munro S, Montgelard C, Pardini AT, Robinson TJ. Matthee CA, et al. Mol Phylogenet Evol. 2007 Mar;42(3):827-37. doi: 10.1016/j.ympev.2006.10.002. Epub 2006 Oct 11. Mol Phylogenet Evol. 2007. PMID: 17101283 - Meta-analysis of indels causing human genetic disease: mechanisms of mutagenesis and the role of local DNA sequence complexity.
Chuzhanova NA, Anassis EJ, Ball EV, Krawczak M, Cooper DN. Chuzhanova NA, et al. Hum Mutat. 2003 Jan;21(1):28-44. doi: 10.1002/humu.10146. Hum Mutat. 2003. PMID: 12497629 - Empirical and structural models for insertions and deletions in the divergent evolution of proteins.
Benner SA, Cohen MA, Gonnet GH. Benner SA, et al. J Mol Biol. 1993 Feb 20;229(4):1065-82. doi: 10.1006/jmbi.1993.1105. J Mol Biol. 1993. PMID: 8445636 - Small insertions and deletions (INDELs) in human genomes.
Mullaney JM, Mills RE, Pittard WS, Devine SE. Mullaney JM, et al. Hum Mol Genet. 2010 Oct 15;19(R2):R131-6. doi: 10.1093/hmg/ddq400. Epub 2010 Sep 21. Hum Mol Genet. 2010. PMID: 20858594 Free PMC article. Review. - Rapid turnover of functional sequence in human and other genomes.
Ponting CP, Nellåker C, Meader S. Ponting CP, et al. Annu Rev Genomics Hum Genet. 2011;12:275-99. doi: 10.1146/annurev-genom-090810-183115. Annu Rev Genomics Hum Genet. 2011. PMID: 21721940 Review.
Cited by
- Evolutionary significance of gene expression divergence.
Jordan IK, Mariño-Ramírez L, Koonin EV. Jordan IK, et al. Gene. 2005 Jan 17;345(1):119-26. doi: 10.1016/j.gene.2004.11.034. Epub 2004 Dec 29. Gene. 2005. PMID: 15716085 Free PMC article. - Phosphorylation and cleavage of presenilin-associated rhomboid-like protein (PARL) promotes changes in mitochondrial morphology.
Jeyaraju DV, Xu L, Letellier MC, Bandaru S, Zunino R, Berg EA, McBride HM, Pellegrini L. Jeyaraju DV, et al. Proc Natl Acad Sci U S A. 2006 Dec 5;103(49):18562-7. doi: 10.1073/pnas.0604983103. Epub 2006 Nov 20. Proc Natl Acad Sci U S A. 2006. PMID: 17116872 Free PMC article. - Problems and solutions for estimating indel rates and length distributions.
Cartwright RA. Cartwright RA. Mol Biol Evol. 2009 Feb;26(2):473-80. doi: 10.1093/molbev/msn275. Epub 2008 Nov 28. Mol Biol Evol. 2009. PMID: 19042944 Free PMC article. - Types and rates of sequence evolution at the high-molecular-weight glutenin locus in hexaploid wheat and its ancestral genomes.
Gu YQ, Salse J, Coleman-Derr D, Dupin A, Crossman C, Lazo GR, Huo N, Belcram H, Ravel C, Charmet G, Charles M, Anderson OD, Chalhoub B. Gu YQ, et al. Genetics. 2006 Nov;174(3):1493-504. doi: 10.1534/genetics.106.060756. Epub 2006 Oct 8. Genetics. 2006. PMID: 17028342 Free PMC article. - Armless mitochondrial tRNAs in Enoplea (Nematoda).
Jühling F, Pütz J, Florentz C, Stadler PF. Jühling F, et al. RNA Biol. 2012 Sep;9(9):1161-6. doi: 10.4161/rna.21630. Epub 2012 Sep 1. RNA Biol. 2012. PMID: 23018779 Free PMC article.
References
- Arndt, P.F., Petrov, D.A., and Hwa, T. 2003. Distinct changes of genomic biases in nucleotide substitution at the time of mammalian radiation. Mol. Biol. Evol. 20: 1887–1896. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources