Coalescence of membrane tethers: experiments, theory, and applications - PubMed (original) (raw)
Coalescence of membrane tethers: experiments, theory, and applications
Damien Cuvelier et al. Biophys J. 2005 Apr.
Abstract
Tethers are nanocylinders of lipid bilayer membrane, arising in situations ranging from micromanipulation experiments on synthetic vesicles to the formation of dynamic tubular networks in the Golgi apparatus. Relying on the extensive theoretical and experimental works aimed to understand the physics of individual tethers formation, we addressed the problem of the interaction between two nanotubes. By using a combination of micropipette manipulation and optical tweezers, we quantitatively studied the process of coalescence that occurred when the separation distance between both vesicle-tether junctions became smaller than a threshold length. Our experiments, which were supported by an original theoretical analysis, demonstrated that the measurements of the tether force and angle between tethers at coalescence directly yield the bending rigidity, kappa, and the membrane tension, sigma, of the vesicles. Contrary to other methods used to probe the bending rigidity of vesicles, the proposed approach permits a direct measurement of kappa without requiring any control of the membrane tension. Finally, after validation of the method and proposal of possible applications, we experimentally investigated the dynamics of the coalescence process.
Figures
FIGURE 1
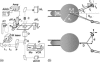
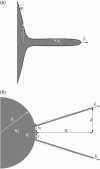
(a) Complete instrumental apparatus assembled around a bright-field inverted microscope. Light from halogen lamp (HL) travels through condenser (C) and illuminates the sample. Objective (O) collects the images, which are captured by analogic camera (aCCD) (25 fps), visualized on control monitor (Mo), and recorded with VCR after image processing (IP). The arbitrary waveform generator (AWG) provides the input signal to high-voltage amplifier (Amp), which drives piezo-element (Pz). Piezo-translator (Pz) is mounted on three-axis micromanipulator (μM1) and sets the vesicle-holding pipette displacement. Aspiration pressure is controlled by adjusting the elevation of a water tank (PT). One bead is held in a pipette that is connected to mechanical micromanipulator _μ_M2. Both _μ_M2 and _μ_M1 are mounted on the stage of the microscope. The second bead is trapped by optical tweezer, which is created by steering light from infrared laser (IR laser) into the microscope via external optics including lenses (L1 and L2), periscope (P), and dichroic mirror (D). (b) Schematic of experimental design. (Top) A vesicle (radius _R_v) is aspirated in a pipette (diameter 2_R_p). Two tethers were extracted from the vesicle, respectively, with the micromanipulated and the optically trapped bead. Length of the nanotubes is _L_t. Tether force, _f_t, is monitored by optical tracking of the x and y components of bead displacement. In this “V” configuration, the half-angle between both tethers is θ. In the Theory section, we used the notation _θ_0 for the half-angle between the two radial directions (from the centers of the beads to the center of the vesicle). The vesicle is retracted, which induces a diminution of _θ_0, down to a value _θ_0,c when coalescence occurs. (Bottom) when both tethers merge, a “Y” configuration is reached. D and d are the distances that are experimentally measured and will serve for analysis.
FIGURE 2
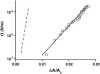
Bending rigidity measurements by micropipette aspiration. Semilog plot of tension versus apparent area expansion. Squares are data points obtained for vesicles made from EPC/mPEG-DOPE/DSPE-PEG-biotin (95:4.995:0.005) over tensions from 10−7 to 10−5 N/m using the micropipette aspiration technique. The exponential rise of tension with area expansion reveals the regime dominated by thermal fluctuations. The solid line is a fit using Eq. 2. The slope yields the bending rigidity κ = 11.8 kBT. The dashed line corresponds to the hypothetical variation of tension as a function of area expansion for more rigid vesicles (typically in a liquid-ordered state) (κ = 70 kBT). Because the low-tension regime is only accessible for area expansion lower than 0.01, direct measurement of κ for liquid-ordered vesicles is not possible by this method.
FIGURE 3
Extraction of a single-membrane tether using an optical trap. (a) Plots of measured force versus time for fluid (“liquid-disordered”) vesicles made of EPC/mPEG-DOPE/DSPE-PEG-biotin (95:4.995:0.005) (solid curve) and for liquid-ordered vesicles made of BSM/cholesterol/mPEG-DOPE/DSPE-PEG-biotin (47.5:47.5:4.995:0.005) (dotted line). Tube extraction and retraction are recorded consecutively (end of extraction cycle marked by the vertical dashed line). See text for details. (b) Plot of the tether force f as a function of the square root of membrane tension σ averaged over 10 vesicles made of EPC/mPEG-DOPE/DSPE-PEG-biotin (95:4.995:0.005). The variation is linear, as predicted by Eq. 3. The slope of the linear fit (dashed line) yields the bending rigidity: κ = 12 ± 1 kBT.
FIGURE 4
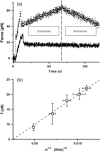
Tether coalescence. (a) Videomicrographs of the experimental arrangement. The vesicle is aspirated in the left pipette. Two beads serve as handles to extrude tethers from the vesicle. A bead held in a pipette is maneuvered with a micromanipulator. The second bead is trapped in a fixed optical tweezer. The upper image shows the “V” configuration, before tube coalescence. The vesicle-holding pipette is retracted until coalescence is triggered. The lower image shows the equilibrium “Y” configuration reached after coalescence. Scale bar is 5 _μ_m. (b) Plot of the coalescence angle, _θ_c, versus membrane tension for two fluid vesicles (EPC/mPEG-DOPE/DSPE-PEG-biotin (95:4.995:0.005)) of different radii (open squares, _R_0 = 13 _μ_m; solid squares, _R_0 = 7.5 _μ_m). (c) Typical temporal evolution of the tether force during tubes extraction and coalescence (marked by asterisk symbol). The vesicle was made from EPC/mPEG-DOPE/DSPE-PEG-biotin (95:4.995:0.005) and aspirated at σ = 5 × 10−5 N/m. The inset shows the x and y components of the tether force, as derived from the _x_-y optical tracking of the bead position. The drop in _f_x and the increase in _f_y reflect the sudden change in tether orientation after coalescence. The overall tether force after coalescence, is the same as before coalescence because the membrane tension is set constant by micropipette aspiration.
FIGURE 5
(a) Qualitative profile of a membrane deformed by the extraction of a tether of radius _R_t with a force _f_t. The angle ϕ denotes the absolute angle between the membrane surface and a plane perpendicular to the tether axis, which is located at a distance r. (b) Notations defining the relevant geometric parameters. D and d are the experimentally measured distances that allow us to calculate the angle θ and the half-separation s between vesicle-tether junctions. and _s_0 are the corresponding angle and half-separation in the absence of any surface mediated interaction. _R_v is the vesicle radius.
FIGURE 6
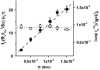
Plot of (solid squares) and
(open circles) versus membrane tension for vesicles made from EPC/mPEG-DOPE/DSPE-PEG-biotin (95:4.995:0.005). Note that _R_v was actually corrected by a geometric factor, (1 + _R_v/_L_t), which is not negligible for tubes that are not much longer than the size of the vesicle (see Theory section for details); _f_t is the tether force at coalescence. As expected from Eqs. 15 and 16,
yields σ, whereas
represents κ.
FIGURE 7
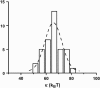
Histogram of bending moduli as derived from for liquid-ordered vesicles (BSM/cholesterol/mPEG-DOPE/DSPE-PEG-biotin (47.5:47.5:4.995:0.005)). The peak value is κ = 66 ± 1 kBT.
FIGURE 8
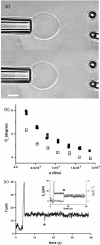
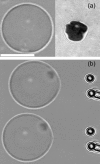
Application of the coalescence method to the measurement of adhesion energies of vesicles. (a, left videomicrograph) Phase contrast image of the equatorial plane of an adhered vesicle (EPC/mPEG-DOPE/DSPE-PEG-biotin (95:4.995:0.005)). (a, right micrograph) RICM image of the contact zone with the substrate for the same vesicle. Contact radius is measured from the size of the dark spot. (b) Extraction and coalescence of two tethers from the adhered vesicle. The microscope stage is moved toward the left. Scale bar is 10 _μ_m.
FIGURE 9
Dynamics of coalescence. (a_–_g) Snapshots of tube merging taken at video rate (Δ_t_ = 40 ms). Scale bar is 5 _μ_m. (h) Temporal evolution of the position of the three-tube junction during the coalescence process. Initial propagation speed is 80 _μ_m/s.
Similar articles
- Fluid-membrane tethers: minimal surfaces and elastic boundary layers.
Powers TR, Huber G, Goldstein RE. Powers TR, et al. Phys Rev E Stat Nonlin Soft Matter Phys. 2002 Apr;65(4 Pt 1):041901. doi: 10.1103/PhysRevE.65.041901. Epub 2002 Mar 13. Phys Rev E Stat Nonlin Soft Matter Phys. 2002. PMID: 12005867 Review. - Distinct membrane mechanical properties of human mesenchymal stem cells determined using laser optical tweezers.
Titushkin I, Cho M. Titushkin I, et al. Biophys J. 2006 Apr 1;90(7):2582-91. doi: 10.1529/biophysj.105.073775. Epub 2006 Jan 6. Biophys J. 2006. PMID: 16399828 Free PMC article. - Effect of salicylate on the elasticity, bending stiffness, and strength of SOPC membranes.
Zhou Y, Raphael RM. Zhou Y, et al. Biophys J. 2005 Sep;89(3):1789-801. doi: 10.1529/biophysj.104.054510. Epub 2005 Jun 10. Biophys J. 2005. PMID: 15951377 Free PMC article. - Influence of thermally driven surface undulations on tethers formed from bilayer membranes.
Glassinger E, Raphael RM. Glassinger E, et al. Biophys J. 2006 Jul 15;91(2):619-25. doi: 10.1529/biophysj.105.068270. Epub 2006 Apr 28. Biophys J. 2006. PMID: 16648163 Free PMC article. - Flexoelectricity of model and living membranes.
Petrov AG. Petrov AG. Biochim Biophys Acta. 2002 Mar 19;1561(1):1-25. doi: 10.1016/s0304-4157(01)00007-7. Biochim Biophys Acta. 2002. PMID: 11988178 Review.
Cited by
- Stereocilia membrane deformation: implications for the gating spring and mechanotransduction channel.
Powers RJ, Roy S, Atilgan E, Brownell WE, Sun SX, Gillespie PG, Spector AA. Powers RJ, et al. Biophys J. 2012 Jan 18;102(2):201-10. doi: 10.1016/j.bpj.2011.12.022. Biophys J. 2012. PMID: 22339856 Free PMC article. - The fluid membrane determines mechanics of erythrocyte extracellular vesicles and is softened in hereditary spherocytosis.
Vorselen D, van Dommelen SM, Sorkin R, Piontek MC, Schiller J, Döpp ST, Kooijmans SAA, van Oirschot BA, Versluijs BA, Bierings MB, van Wijk R, Schiffelers RM, Wuite GJL, Roos WH. Vorselen D, et al. Nat Commun. 2018 Nov 23;9(1):4960. doi: 10.1038/s41467-018-07445-x. Nat Commun. 2018. PMID: 30470753 Free PMC article. - Curvature-driven lipid sorting in biomembranes.
Callan-Jones A, Sorre B, Bassereau P. Callan-Jones A, et al. Cold Spring Harb Perspect Biol. 2011 Feb 1;3(2):a004648. doi: 10.1101/cshperspect.a004648. Cold Spring Harb Perspect Biol. 2011. PMID: 21421916 Free PMC article. Review. - Optical stretching of giant unilamellar vesicles with an integrated dual-beam optical trap.
Solmaz ME, Biswas R, Sankhagowit S, Thompson JR, Mejia CA, Malmstadt N, Povinelli ML. Solmaz ME, et al. Biomed Opt Express. 2012 Oct 1;3(10):2419-27. doi: 10.1364/BOE.3.002419. Epub 2012 Sep 7. Biomed Opt Express. 2012. PMID: 23082284 Free PMC article. - Nonaxisymmetric Shapes of Biological Membranes from Locally Induced Curvature.
Omar YAD, Sahu A, Sauer RA, Mandadapu KK. Omar YAD, et al. Biophys J. 2020 Sep 15;119(6):1065-1077. doi: 10.1016/j.bpj.2020.07.021. Epub 2020 Jul 31. Biophys J. 2020. PMID: 32860742 Free PMC article.
References
- Angelova, M. I., and D. S. Dimitrov. 1988. A mechanism of liposome electroformation. Prog. Colloid Poymr. Sci. 76:59–67.
- Brochard, F., and J. F. Lennon. 1975. Frequency spectrum of the flicker phenomenon in erythrocytes. J. Phys. (Paris). 36:1035–1047.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources