Spatiotemporal image correlation spectroscopy (STICS) theory, verification, and application to protein velocity mapping in living CHO cells - PubMed (original) (raw)
Spatiotemporal image correlation spectroscopy (STICS) theory, verification, and application to protein velocity mapping in living CHO cells
Benedict Hebert et al. Biophys J. 2005 May.
Abstract
We introduce a new extension of image correlation spectroscopy (ICS) and image cross-correlation spectroscopy (ICCS) that relies on complete analysis of both the temporal and spatial correlation lags for intensity fluctuations from a laser-scanning microscopy image series. This new approach allows measurement of both diffusion coefficients and velocity vectors (magnitude and direction) for fluorescently labeled membrane proteins in living cells through monitoring of the time evolution of the full space-time correlation function. By using filtering in Fourier space to remove frequencies associated with immobile components, we are able to measure the protein transport even in the presence of a large fraction (>90%) of immobile species. We present the background theory, computer simulations, and analysis of measurements on fluorescent microspheres to demonstrate proof of principle, capabilities, and limitations of the method. We demonstrate mapping of flow vectors for mixed samples containing fluorescent microspheres with different emission wavelengths using space time image cross-correlation. We also present results from two-photon laser-scanning microscopy studies of alpha-actinin/enhanced green fluorescent protein fusion constructs at the basal membrane of living CHO cells. Using space-time image correlation spectroscopy (STICS), we are able to measure protein fluxes with magnitudes of mum/min from retracting lamellar regions and protrusions for adherent cells. We also demonstrate the measurement of correlated directed flows (magnitudes of mum/min) and diffusion of interacting alpha5 integrin/enhanced cyan fluorescent protein and alpha-actinin/enhanced yellow fluorescent protein within living CHO cells. The STICS method permits us to generate complete transport maps of proteins within subregions of the basal membrane even if the protein concentration is too high to perform single particle tracking measurements.
Figures
FIGURE 1
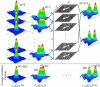
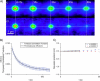
Schematic illustration of the algorithm used to compute the discrete approximation to a generalized spatiotemporal correlation function for a simulated system with flow and diffusion. The Gaussian autocorrelation peaks for each image are shown in the left column (Δ_t_ = 0), the cross-correlation for a lag-time of 1 time-unit in the middle column (Δ_t_ = 1), and for the second longest lag-time of N_–1 time-units in the right column (Δ_t = N_−1, where N is the number of frames in the image series). The open arrows on the simulation images represent the direction of the flow. The averaged Gaussian correlation functions r_′aa(ξ, η, Δ_t) are shown at the bottom for Δ_t = 0,1 and _N_–1. The separation of the Gaussian correlation peak due to flow (FG) from the Gaussian correlation peak arising from the diffusing population (DG) is clearly seen.
FIGURE 2
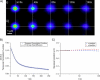
STICS and ICS analysis results for computer-generated simulations. (A) A contour plot of the STICS correlation functions for the case of i), flow (_v_x = −0.12 _μ_m/s and _v_y = 0.08 _μ_m/s); ii), diffusion (D = 0.01 _μ_m2/s); and iii), two-populations' flow and diffusion (_v_x = −0.12 _μ_m/s, _v_y = 0.08 _μ_m/s, and D = 0.01 _μ_m2/s). (B) The ICS temporal autocorrelation functions (Eq. 4) and best fits for the same simulations. (C) Plots of the peak position of the STICS Gaussian correlation peaks from A as a function of time. The peak position versus time gives an estimate of the concerted velocity of the particles in case i, of _v_x = −0.119 ± 0.002 _μ_m/s and _v_y = 0.0792 ± 0.0005 _μ_m/s and in case iii, of _v_x = −0.096 ± 0.007 _μ_m/s and _v_y = 0.068 ± 0.006 _μ_m/s, respectively. All simulations were 128 × 128 pixels with 500 frames at a density of 50 particles/_μ_m2, using 0.02 s/frame, 0.06 _μ_m/pixel, and an _e_−2 radius of 0.4 _μ_m.
FIGURE 3
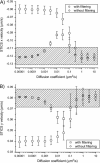
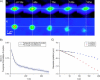
STICS analysis results for computer simulations of two populations, one flowing (_v_x = −0.12 _μ_m/s and _v_y = 0.08 _μ_m/s) and one diffusing (varying diffusion coefficients). (A) The x velocity as resolved by STICS with and without the immobile population filtering. (B) The y velocity as resolved by STICS with and without the immobile population filtering. On both graphs, each point and error bar represents the average result of 100 simulations with standard deviation. The shaded regions show the set velocities in the simulation with an acceptable error of ±10%. The computer simulations were 128 × 128 pixels with 100 frames at a density of 100 particles/_μ_m2, using 0.1 s/frame, 0.06 _μ_m/pixel, and an _e_−2 radius of 0.4 _μ_m.
FIGURE 4
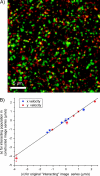
(A) A composite image of fluorescent microspheres consisting of two different fluorescent particle populations (red and green) and an added interacting particle population (yellow overlap). The composite image was made by adding an independent image of fluorescent spheres (our artificial interacting population) to both detection channel images. For each image time-series constructed, the velocities of the non-interacting populations remained constant whereas the interacting fraction's direction of flow was systematically changed. (B) A plot of the interacting population velocity magnitudes in x and y measured by STICS in the composite image series (i.e., with the added population and the red and green microspheres present) versus the velocity magnitude of the introduced interacting population measured by STICS in its original image series (i.e., without the red and green particles present).
FIGURE 5
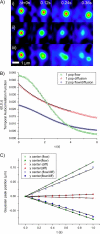
Two-photon LSM images of the basal membrane of CHO cells expressing EGFP-labeled _α_-actinin. The regions analyzed with ICS and STICS are shown as open squares and the STICS analysis results are shown in Figs. 5–7. (A) A 642 pixel region where the temporal autocorrelation function is best fit to a single-population diffusion model (Eq. 5). (B) A 1282 pixel region where the temporal autocorrelation function is best fit to a two-population flow/diffusion model (Eq. 8). (C) A 1282 pixel region where the temporal autocorrelation function is best fit to a two-population flow/diffusion model (Eq. 8). All images are 512 × 480 pixels at a resolution of 0.118 _μ_m/pixel, and a total of 180, 360, and 120 frames at a resolution of 5, 5, and 15 s/frame for A_–_C, respectively.
FIGURE 6
In vivo ICS and STICS analysis of protein diffusion in a peripheral basal membrane region of a CHO cell (Fig. 5 A) expressing EGFP-labeled _α_-actinin. (A) Contour plots of space-time correlation functions from STICS analysis (Eq. 11) as a function of lag-time for i) with and ii) without the immobile population contribution present. (B) A plot of the ICS temporal autocorrelation function and best fit to a single-population diffusion model (Eq. 5). The recovered diffusion coefficient was D = (9 ± 1) × 10−4 _μ_m2/s. (C) Peak tracking plot of the STICS correlation peaks reveals that they stay centered at zero spatial lags, within the precision of our measurement.
FIGURE 7
In vivo ICS and STICS analysis of protein flux in random directions in a peripheral basal membrane region of a CHO cell (Fig. 5 B) expressing EGFP-labeled _α_-actinin. (A) Contour plots of space-time correlation functions from STICS analysis as a function of time for i) with and ii) without the immobile population contribution present. (B) A plot of the ICS temporal autocorrelation function and best fit to a two-population flow/diffusion model (Eq. 8). The recovered ICS velocity and diffusion were _v_ICS = (13 ± 1) × 10−3 _μ_m/s and D = (8 ± 1) × 10−4 _μ_m2/s. (C) Peak tracking plot of the STICS correlation peaks reveals that they stay centered at zero spatial lags, within the precision of our measurement, yielding a very small velocity of _v_STICS = (1.1 ± 0.7) × 10−3 _μ_m/s.
FIGURE 8
In vivo ICS and STICS analysis of directed protein flow in a peripheral basal membrane region of a CHO cell (Fig. 5 C) expressing EGFP-labeled _α_-actinin. (A) Contour plots of space-time correlation functions from STICS analysis as a function of time for i) with and ii) without the immobile population contribution present. (B) A plot of the ICS temporal autocorrelation function and best fit to a two-population flow/diffusion model (Eq. 8). The recovered velocity was _v_ICS = (7.7 ± 0.8) × 10−3 _μ_m/s and a small diffusion coefficient was measured: D = (6 ± 1) × 10−5 _μ_m2/s. (C) Peak tracking plot of the STICS correlation peaks (after the immobile population removal) shows a net displacement of the Gaussian center, yielding velocities of _v_x = (1.8 ± 0.3) × 10−3 and _v_y = (5.5 ± 0.2) × 10−3 _μ_m/s.
FIGURE 9
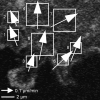
Two-photon STICS velocity map image of EGFP/_α_-actinin flux in the vicinity of a retracting lamellar extension in a CHO cell plated on fibronectin. The original image-series reveals that the extended lamellar protrusions are retracting. Selecting regions of 16 × 16 or 32 × 32 pixels and performing the STICS analysis reveals a net flow of the _α_-actinin toward the cell interior (arrows). The spatial scale is shown as a bar and the velocity scale is shown as an arrow. The original image-dimensions are 512 × 480 pixels at 0.118 _μ_m/pixel and a total of 120 images at 5 s/frame.
FIGURE 10
Two-photon auto- and cross-correlation STICS velocity map images of ECFP/_α_-actinin and EGFP/_α_5 integrin at the basal membrane of a CHO cell on a fibronectin substrate. (A) STICS velocity map for ECFP/_α_-actinin (channel 1); (B) STICS velocity map for EYFP/_α_5 integrin (channel 2); and (C) two-color STICCS velocity map of channel 1 with channel 2 showing flow vectors for co-transported ECFP/_α_-actinin and EGFP/_α_5 integrin. The spatial scale is shown as a bar and the velocity scale is shown as an arrow. The original image dimensions are 512 × 480 pixels at 0.118 _μ_m/pixel and a total of 120 images at 5 s/frame.
Similar articles
- k-Space image correlation spectroscopy: a method for accurate transport measurements independent of fluorophore photophysics.
Kolin DL, Ronis D, Wiseman PW. Kolin DL, et al. Biophys J. 2006 Oct 15;91(8):3061-75. doi: 10.1529/biophysj.106.082768. Epub 2006 Jul 21. Biophys J. 2006. PMID: 16861272 Free PMC article. - Sampling effects, noise, and photobleaching in temporal image correlation spectroscopy.
Kolin DL, Costantino S, Wiseman PW. Kolin DL, et al. Biophys J. 2006 Jan 15;90(2):628-39. doi: 10.1529/biophysj.105.072322. Epub 2005 Oct 28. Biophys J. 2006. PMID: 16258048 Free PMC article. - Advances in image correlation spectroscopy: measuring number densities, aggregation states, and dynamics of fluorescently labeled macromolecules in cells.
Kolin DL, Wiseman PW. Kolin DL, et al. Cell Biochem Biophys. 2007;49(3):141-64. doi: 10.1007/s12013-007-9000-5. Epub 2007 Oct 2. Cell Biochem Biophys. 2007. PMID: 17952641 Review. - Two-photon image correlation spectroscopy and image cross-correlation spectroscopy.
Wiseman PW, Squier JA, Ellisman MH, Wilson KR. Wiseman PW, et al. J Microsc. 2000 Oct;200(Pt 1):14-25. doi: 10.1046/j.1365-2818.2000.00736.x. J Microsc. 2000. PMID: 11012824 - Quantifying spatial and temporal variations of the cell membrane ultra-structure by bimFCS.
Jin W, Simsek MF, Pralle A. Jin W, et al. Methods. 2018 May 1;140-141:151-160. doi: 10.1016/j.ymeth.2018.02.019. Epub 2018 Mar 9. Methods. 2018. PMID: 29530504 Free PMC article. Review.
Cited by
- Two-photon time-lapse microscopy of BODIPY-cholesterol reveals anomalous sterol diffusion in chinese hamster ovary cells.
Lund FW, Lomholt MA, Solanko LM, Bittman R, Wüstner D. Lund FW, et al. BMC Biophys. 2012 Oct 18;5:20. doi: 10.1186/2046-1682-5-20. BMC Biophys. 2012. PMID: 23078907 Free PMC article. - Development of an image Mean Square Displacement (iMSD)-based method as a novel approach to study the intracellular trafficking of nanoparticles.
Digiacomo L, Digman MA, Gratton E, Caracciolo G. Digiacomo L, et al. Acta Biomater. 2016 Sep 15;42:189-198. doi: 10.1016/j.actbio.2016.07.031. Epub 2016 Jul 20. Acta Biomater. 2016. PMID: 27449340 Free PMC article. - Advanced Fluorescence Microscopy Methods to Study Dynamics of Fluorescent Proteins In Vivo.
Díaz M, Malacrida L. Díaz M, et al. Methods Mol Biol. 2023;2564:53-74. doi: 10.1007/978-1-0716-2667-2_3. Methods Mol Biol. 2023. PMID: 36107337 - A Fluorescence Correlation Spectrometer for Measurements in Cuvettes.
Sahoo B, Sil TB, Karmakar B, Garai K. Sahoo B, et al. Biophys J. 2018 Aug 7;115(3):455-466. doi: 10.1016/j.bpj.2018.05.038. Biophys J. 2018. PMID: 30089243 Free PMC article. - Quantitative measurement of intracellular transport of nanocarriers by spatio-temporal image correlation spectroscopy.
Coppola S, Pozzi D, De Sanctis SC, Digman MA, Gratton E, Caracciolo G. Coppola S, et al. Methods Appl Fluoresc. 2013;1(1):10.1088/2050-6120/1/1/015005. doi: 10.1088/2050-6120/1/1/015005. Methods Appl Fluoresc. 2013. PMID: 24376913 Free PMC article.
References
- Brown, C. M., and N. O. Petersen. 1998. An image correlation analysis of the distribution of clathrin-associated adaptor protein (AP-2) at the plasma membrane. J. Cell Sci. 111:271–281. - PubMed
- Dittrich, P. S., and P. Schwille. 2002. Spatial two-photon fluorescence cross-correlation spectroscopy for controlling molecular transport in microfluidic structures. Anal. Chem. 74:4472–4479. - PubMed
- Elson, E. L., and D. Magde. 1974. Fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers. 13:1–27. - PubMed
- Lauffenburger, D. A., and A. F. Horwitz. 1996. Cell migration: a physically integrated molecular process. Cell. 84:359–369. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources