Joint modeling of linkage and association: identifying SNPs responsible for a linkage signal - PubMed (original) (raw)

Comparative Study

doi: 10.1086/430277. Epub 2005 Apr 5.

Affiliations

Comparative Study

Joint modeling of linkage and association: identifying SNPs responsible for a linkage signal

Mingyao Li et al. Am J Hum Genet. 2005 Jun.

Abstract

Once genetic linkage has been identified for a complex disease, the next step is often association analysis, in which single-nucleotide polymorphisms (SNPs) within the linkage region are genotyped and tested for association with the disease. If a SNP shows evidence of association, it is useful to know whether the linkage result can be explained, in part or in full, by the candidate SNP. We propose a novel approach that quantifies the degree of linkage disequilibrium (LD) between the candidate SNP and the putative disease locus through joint modeling of linkage and association. We describe a simple likelihood of the marker data conditional on the trait data for a sample of affected sib pairs, with disease penetrances and disease-SNP haplotype frequencies as parameters. We estimate model parameters by maximum likelihood and propose two likelihood-ratio tests to characterize the relationship of the candidate SNP and the disease locus. The first test assesses whether the candidate SNP and the disease locus are in linkage equilibrium so that the SNP plays no causal role in the linkage signal. The second test assesses whether the candidate SNP and the disease locus are in complete LD so that the SNP or a marker in complete LD with it may account fully for the linkage signal. Our method also yields a genetic model that includes parameter estimates for disease-SNP haplotype frequencies and the degree of disease-SNP LD. Our method provides a new tool for detecting linkage and association and can be extended to study designs that include unaffected family members.

PubMed Disclaimer

Figures

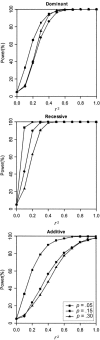
Figure 1

Figure 1

Power to reject linkage equilibrium (

_r_2=0

). Results are based on 2,000 replicates of 500 ASPs. All models have population disease prevalence K = 2% and sibling recurrence-risk ratio

λ_s_=1.1

. Power was assessed at the 5% level.

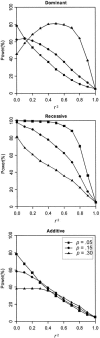
Figure 2

Figure 2

Power to reject complete LD (

_r_2=1

). Results are based on 2,000 replicates of 500 ASPs. All models have population disease prevalence K = 2% and sibling recurrence-risk ratio

λ_s_=1.3

. Power was assessed at the 5% level.

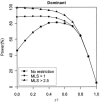
Figure 3

Figure 3

Impact of linkage evidence on test of complete LD. Results are based on 2,000 replicates of 500 ASPs under a dominant model with population disease prevalence K = 2%, allele frequency

p _D_=p _A_=0.30

, and sibling recurrence-risk ratio

λ_s_=1.3

. Power was assessed at the 5% level.

Figure 4

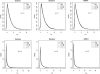
Figure 4

Impact of the number of flanking markers. Results are based on 2,000 replicates of 500 ASPs simulated under an additive model with population disease prevalence K = 2%, allele frequency

p _D_=p _A_=0.15

, and sibling recurrence-risk ratios

λ_s_=1.1

(A) and 1.3 (B). Data were simulated using 10 flanking markers, each with two equally frequent alleles. Intermarker recombination fraction is 0.1. Power was assessed at the 5% level.

Figure 5

Figure 5

Impact of heterozygosity of flanking markers. Results are based on 2,000 replicates of 500 ASPs simulated under an additive model with population disease prevalence K = 2%, allele frequency

p _D_=p _A_=0.15

, and sibling recurrence-risk ratios

λ_s_=1.1

(A) and 1.3 (B). Data were simulated using two flanking markers, each with two, four, or eight equally frequent alleles. Intermarker recombination fraction is 0.1. Power was assessed at the 5% level.

Figure 6

Figure 6

Impact of intermarker recombination of flanking markers. Results are based on 2,000 replicates of 500 ASPs simulated under an additive model with population disease prevalence K = 2%, allele frequency

p _D_=p _A_=0.15

, and sibling recurrence-risk ratios

λ_s_=1.1

(A) and 1.3 (B). Data were simulated using 10 flanking markers, each with four equally frequent alleles. Power was assessed at the 5% level.

Figure 7

Figure 7

Comparison of empirical null distributions. Results are based on 2,000 replicates of 500 ASPs. All models have population disease prevalence K = 2% and allele frequency

p _D_=p _A_=0.15

. The solid line in each plot is the density of the empirical null distribution simulated using true parameter values of the disease model. Dashed lines are density plots of the empirical null distributions generated using the resampling procedures described in the “Methods” section. The empirical null distribution was generated for each level of disease-SNP LD.

Similar articles

Cited by

References

Electronic-Database Information

    1. University of Michigan Center for Statistical Genetics, http://csg.sph.umich.edu/

References

    1. Abecasis GR, Cardon LR, Cookson WO (2000a) A general test of association for quantitative traits in nuclear families. Am J Hum Genet 66:279–292 - PMC - PubMed
    1. Abecasis GR, Cookson WO, Cardon LR (2000b) Pedigree tests of transmission disequilibrium. Eur J Hum Genet 8:545–55110.1038/sj.ejhg.5200494 - DOI - PubMed
    1. Allison DB (1997) Transmission disequilibrium tests for quantitative traits. Am J Hum Genet 60:676–690 - PMC - PubMed
    1. Baum LE (1972) An inequality and associated maximization technique in statistical estimation for probabilistic functions of Markov processes. Inequalities 3:1–8
    1. Boehnke M, Langefeld CD (1998) Genetic association mapping based on discordant sib pairs: the discordant-alleles test. Am J Hum Genet 62:950–961 - PMC - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources