Physical limits to biochemical signaling - PubMed (original) (raw)

Physical limits to biochemical signaling

William Bialek et al. Proc Natl Acad Sci U S A. 2005.

Abstract

Many crucial biological processes operate with surprisingly small numbers of molecules, and there is renewed interest in analyzing the impact of noise associated with these small numbers. Twenty-five years ago, Berg and Purcell showed that bacterial chemotaxis, where a single-celled organism must respond to small changes in concentration of chemicals outside the cell, is limited directly by molecule counting noise and that aspects of the bacteria's behavioral and computational strategies must be chosen to minimize the effects of this noise. Here, we revisit and generalize their arguments to estimate the physical limits to signaling processes within the cell and argue that recent experiments are consistent with performance approaching these limits.

PubMed Disclaimer

Figures

Fig. 1.

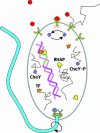
Fig. 1.

Measuring the concentration of a signaling molecule by a biological sensor, which in turn controls downstream events, is a generic task. Here, several examples are depicted schematically for E. coli. Binding of attractant/repellent molecules to a surface receptor complex modulates the rate of autophosphorylation of the associated kinase. This change in kinase activity results in a corresponding concentration change of the internal signaling molecule, CheY∼P, that controls the direction of flagellar motor rotation. Also shown is transcription initiation, where the promoter region can be regarded as a sensor for transcription factors (TF). These proteins, whose concentrations vary depending on the cell cycle and external cues, determine whether or not RNA polymerase (RNAP) turns on a gene.

Fig. 2.

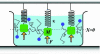
Fig. 2.

For the mass-spring system immersed in a viscous fluid, measuring the linear response of the position, X(t), to a known, small external force, F(t), determines the generalized susceptibility. From this susceptibility, the fluctuation-dissipation theorem can be used to obtain the power spectrum of fluctuations in the closed system at equilibrium, as in Eq. 11. These fluctuations provide a lower bound on the accuracy of any measurement of the position. If measurements are carried out on N identical mass-spring systems, the expected error is reduced by a factor of 1/formula image. However, as N increases, this improvement ceases to hold, as neighboring mass-spring systems become physically close enough to experience correlated fluctuations from collisions with the particle bath, as shown. These correlations have been measured for two optically trapped colloidal particles (16).

Fig. 3.

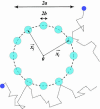
Fig. 3.

Schematic representation of a cluster of m receptors of size b, distributed uniformly on a ring of size a. For a ≫ b, the relative accuracy in measurement of the substrate concentration improves as 1/formula image until mb ∼ a, at which point the binding/unbinding events of nearby receptors are no longer independent.

Similar articles

Cited by

References

    1. Schrödinger, E. (1944) What is Life? (Cambridge Univ. Press, Cambridge, U.K.).
    1. Rieke, F. & Baylor, D. A. (1998) Rev. Mod. Phys. 70 1027-1036.
    1. Boeckh, J., Kaissling, K. E. & Schneider, D. (1965) Cold Spring Harbor Symp. Quant. Biol. 30 263-281. - PubMed
    1. Barlow, H. B. (1981) Proc. R. Soc. London B 212 1-34. - PubMed
    1. Rieke, F., Warland, D., de Ruyter van Stevenick, R. & Bialek, W. (1997) Spikes: Exploring the Neural Code (MIT Press, Cambridge, MA).

Publication types

MeSH terms

Substances

LinkOut - more resources