Imitation dynamics predict vaccinating behaviour - PubMed (original) (raw)
Imitation dynamics predict vaccinating behaviour
Chris T Bauch. Proc Biol Sci. 2005.
Abstract
There exists an interplay between vaccine coverage, disease prevalence and the vaccinating behaviour of individuals. Moreover, because of herd immunity, there is also a strategic interaction between individuals when they are deciding whether or not to vaccinate, because the probability that an individual becomes infected depends upon how many other individuals are vaccinated. To understand this potentially complex interplay, a game dynamic model is developed in which individuals adopt strategies according to an imitation dynamic (a learning process), and base vaccination decisions on disease prevalence and perceived risks of vaccines and disease. The model predicts that oscillations in vaccine uptake are more likely in populations where individuals imitate others more readily or where vaccinating behaviour is more sensitive to changes in disease prevalence. Oscillations are also more likely when the perceived risk of vaccines is high. The model reproduces salient features of the time evolution of vaccine uptake and disease prevalence during the whole-cell pertussis vaccine scare in England and Wales during the 1970s. This suggests that using game theoretical models to predict, and even manage, the population dynamics of vaccinating behaviour may be feasible.
Figures
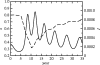
Figure 1
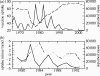
(a) Pertussis vaccine uptake (dashed) and case notifications (solid) in England and Wales from 1967 to 2003 and (b) pertussis vaccine uptake minus a linear least-squares fit (dashed) and case notifications (black) in England and Wales from 1979 to 1993. The vaccine uptake datum at year t is the proportion of children born in year _t_−2 who completed the recommended course of pertussis immunizations by year t, and the case notification datum at year t is simply the total number of cases reported in that year. Data are from the WHO (2004) and Miller & Gay (1997).
Figure 2
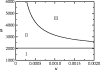
The κ–ω parameter plane for the vaccination game with imitation dynamics, equations (2.10)–(2.12). See text for description of regions I, II and III. Along the Hopf curve dividing regions II and III, κ(_ω_−_ω_0) is a constant. The line _ω_=_ω_0 divides regions I and II. Other parameters are R0=10, 1/_γ_=10 days, 1/_μ_=50 years.
Figure 3
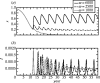
Representative time-series of x, (a) the frequency of vaccinators, and (b) I, the disease prevalence, from regions I, II and III of the κ–ω parameter plane, for three values of ω. Other parameters are 1/_μ_=50 years, 1/_γ_=10 days, R0=10, _κ_=0.001. Initial conditions are _S_=0.05, _I_=0.0001, x_=0.95. Given that immigration of infected individuals becomes important in the inter-epidemic troughs, a term +α is included for these time-series in equation (2.10), and a term −_α in equation (2.12), where _α_=10−8 day−1.
Figure 4
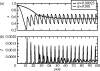
Representative time-series of x, (a) the frequency of vaccinators, and (b) I, the disease prevalence, from regions II and III of the κ–ω parameter plane, for two values of κ. Other parameters are 1/_μ_=50 years, 1/_γ_=10 days, R0=10, _ω_=5000, _α_=10−8 day−1 (see figure 3 caption). Initial conditions are _S_=0.05, _I_=0.0001, _x_=0.95.
Figure 5
A simulated pertussis vaccine scare, with time-series of frequency of vaccinators x (dashed line; equivalent to vaccine uptake in figure 1_a_) and disease prevalence I (solid line; equivalent to case reports in figure 1_a_). Parameters are R0=15, 1/_γ_=22 days, 1/_μ_=50 years, _κ_=0.002, _ω_=5000; these parameter values yield a mean vaccine uptake and period of oscillation similar to that observed in England and Wales before the whole-cell pertussis vaccine scare of the 1970s (figure 1; Bauch & Earn 2003). The population is near the equilibrium E4 at _t_=0 years. At _t_=5 years, the perceived vaccine risk _r_v is increased eightfold in order to produce a decline similar to that observed in England and Wales from 1973 to 1978. At _t_=10 years, the pre-scare value of _r_v is restored.
Similar articles
- A game dynamic model for delayer strategies in vaccinating behaviour for pediatric infectious diseases.
Bhattacharyya S, Bauch CT. Bhattacharyya S, et al. J Theor Biol. 2010 Dec 7;267(3):276-82. doi: 10.1016/j.jtbi.2010.09.005. Epub 2010 Sep 8. J Theor Biol. 2010. PMID: 20831873 - Dynamics of vaccination strategies via projected dynamical systems.
Cojocaru MG, Bauch CT, Johnston MD. Cojocaru MG, et al. Bull Math Biol. 2007 Jul;69(5):1453-76. doi: 10.1007/s11538-006-9173-x. Epub 2007 Jan 18. Bull Math Biol. 2007. PMID: 17235708 - Voluntary vaccination dilemma with evolving psychological perceptions.
Feng X, Wu B, Wang L. Feng X, et al. J Theor Biol. 2018 Feb 14;439:65-75. doi: 10.1016/j.jtbi.2017.11.011. Epub 2017 Dec 13. J Theor Biol. 2018. PMID: 29199090 - [Genetic evolution under vaccine pressure: the Bordetella pertussis model].
Simondon F, Guiso N. Simondon F, et al. Bull Soc Pathol Exot. 2000 Jul;93(3):202-5. Bull Soc Pathol Exot. 2000. PMID: 11030058 Review. French. - Epidemiological determinants of pertussis.
Miller E, Gay NJ. Miller E, et al. Dev Biol Stand. 1997;89:15-23. Dev Biol Stand. 1997. PMID: 9272331 Review.
Cited by
- An evolutionary game modeling to assess the effect of border enforcement measures and socio-economic cost: Export-importation epidemic dynamics.
Kabir KA, Chowdhury A, Tanimoto J. Kabir KA, et al. Chaos Solitons Fractals. 2021 May;146:110918. doi: 10.1016/j.chaos.2021.110918. Epub 2021 Apr 8. Chaos Solitons Fractals. 2021. PMID: 33846669 Free PMC article. - Disease Interventions Can Interfere with One Another through Disease-Behaviour Interactions.
Andrews MA, Bauch CT. Andrews MA, et al. PLoS Comput Biol. 2015 Jun 5;11(6):e1004291. doi: 10.1371/journal.pcbi.1004291. eCollection 2015 Jun. PLoS Comput Biol. 2015. PMID: 26047028 Free PMC article. - Optimizing reactive responses to outbreaks of immunizing infections: balancing case management and vaccination.
Klepac P, Bjørnstad ON, Metcalf CJ, Grenfell BT. Klepac P, et al. PLoS One. 2012;7(8):e41428. doi: 10.1371/journal.pone.0041428. Epub 2012 Aug 10. PLoS One. 2012. PMID: 22899996 Free PMC article. - Optimal time-profiles of public health intervention to shape voluntary vaccination for childhood diseases.
Buonomo B, Manfredi P, d'Onofrio A. Buonomo B, et al. J Math Biol. 2019 Mar;78(4):1089-1113. doi: 10.1007/s00285-018-1303-1. Epub 2018 Nov 2. J Math Biol. 2019. PMID: 30390103 - Disease control through voluntary vaccination decisions based on the smoothed best response.
Xu F, Cressman R. Xu F, et al. Comput Math Methods Med. 2014;2014:825734. doi: 10.1155/2014/825734. Epub 2014 Feb 16. Comput Math Methods Med. 2014. PMID: 24693329 Free PMC article.
References
- Albert M.R, Ostheimer K.G, Breman J.G. The last smallpox epidemic in Boston and the vaccination controversy, 1901–1903. N. Engl. J. Med. 2001;344:375–379. - PubMed
- Anderson R.M, May R.M. Oxford University Press; 1991. Infectious diseases of humans.
- Andre F. Vaccinology: past achievements, present roadblocks and future promises. Vaccine. 2003;21:593–595. - PubMed
- Asch D.A, Baron J, Hershey J.C, Kunreuther H, Meszaros J, Ritov I, Spranca M. Omission bias and pertussis vaccination. Med. Decis. Making. 1994;14:118–123. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical