Gene identification in novel eukaryotic genomes by self-training algorithm - PubMed (original) (raw)

Comparative Study

. 2005 Nov 28;33(20):6494-506.

doi: 10.1093/nar/gki937. Print 2005.

Affiliations

Comparative Study

Gene identification in novel eukaryotic genomes by self-training algorithm

Alexandre Lomsadze et al. Nucleic Acids Res. 2005.

Abstract

Finding new protein-coding genes is one of the most important goals of eukaryotic genome sequencing projects. However, genomic organization of novel eukaryotic genomes is diverse and ab initio gene finding tools tuned up for previously studied species are rarely suitable for efficacious gene hunting in DNA sequences of a new genome. Gene identification methods based on cDNA and expressed sequence tag (EST) mapping to genomic DNA or those using alignments to closely related genomes rely either on existence of abundant cDNA and EST data and/or availability on reference genomes. Conventional statistical ab initio methods require large training sets of validated genes for estimating gene model parameters. In practice, neither one of these types of data may be available in sufficient amount until rather late stages of the novel genome sequencing. Nevertheless, we have shown that gene finding in eukaryotic genomes could be carried out in parallel with statistical models estimation directly from yet anonymous genomic DNA. The suggested method of parallelization of gene prediction with the model parameters estimation follows the path of the iterative Viterbi training. Rounds of genomic sequence labeling into coding and non-coding regions are followed by the rounds of model parameters estimation. Several dynamically changing restrictions on the possible range of model parameters are added to filter out fluctuations in the initial steps of the algorithm that could redirect the iteration process away from the biologically relevant point in parameter space. Tests on well-studied eukaryotic genomes have shown that the new method performs comparably or better than conventional methods where the supervised model training precedes the gene prediction step. Several novel genomes have been analyzed and biologically interesting findings are discussed. Thus, a self-training algorithm that had been assumed feasible only for prokaryotic genomes has now been developed for ab initio eukaryotic gene identification.

PubMed Disclaimer

Figures

Figure 1

Figure 1

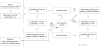
Diagram of hidden states of the HSMM employed in the eukaryotic GeneMark.hmm (E-3.0); only states emitting sequence of the direct DNA strand are shown, while the states generating sequence of the complementary strand (the mirror symmetrical part of the diagram with reversed arrows and horizontal symmetry line crossing ‘intergenic region’ state) are omitted.

Figure 2

Figure 2

The step-wise diagram of the iterative unsupervised parameterization of HSMM implemented in GeneMark.hmm ES-3.0.

Figure 3

Figure 3

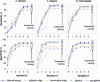
Gene prediction accuracy parameters (Sn and Sp), as determined on the test sets for A.thaliana, C.elegans and D.melanogaster, are shown as functions of the iteration index. For gene predictions produced by models defined at initialization, the Sn and Sp values are shown at zero index value. Upon application of GeneMark.hmm ES-3.0 to genomes of A.gambiae, C.intestinalis, C.reinhardtii and T.gondii we observed similar dynamics of change of the Sn and Sp parameters measured on the relevant test sets (data not shown).

Figure 4

Figure 4

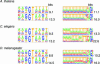
Pictograms of positional nucleotide frequency distributions observed around donor site (left column) and acceptor site (right column). Pictograms of the distributions derived after the first iteration are shown in the top panels of panel pairs, for the distributions derived at the algorithm convergence—in the bottom panels. Values (in bits) of the information content of the first-order positional Markov model derived from the aligned sequences are shown next to the pictograms. (The pictograms were drawn by the software utility available at

).

Figure 5

Figure 5

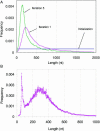
(A) Change of the shape of predicted exon length distribution through iterations (D.melanogaster). Note that the GeneMark ES-3.0 algorithm continues to use uniform exon length distribution in the first three iterations. At convergence point the predicted exon length distribution coincides with the exon length distribution produced by the supervised training (not shown). (B) The shape of the C.intestinalis intron length distribution reached at iterations convergence.

Figure 6

Figure 6

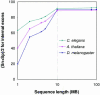
The internal exon prediction accuracy of GeneMark.hmm ES-3.0 characterized by (Sn + Sp)/2, as a function of the length of genomic sequence available for unsupervised training.

Similar articles

Cited by

References

    1. Burge C., Karlin S. Prediction of complete gene structures in human genomic DNA. J. Mol. Biol. 1997;268:78–94. - PubMed
    1. Krogh A. Two methods for improving performance of an HMM and their application for gene finding. Proc. Int. Conf. Intell. Syst. Mol. Biol. 1997;5:179–186. - PubMed
    1. Parra G., Blanco E., Guigo R. GeneID in Drosophila. Genome Res. 2000;10:511–515. - PMC - PubMed
    1. Reese M.G., Kulp D., Tammana H., Haussler D. Genie—gene finding in Drosophila melanogaster. Genome Res. 2000;10:529–538. - PMC - PubMed
    1. Stanke M., Waack S. Gene prediction with a hidden Markov model and a new intron submodel. Bioinformatics. 2003;19:II215–II225. - PubMed

Publication types

MeSH terms

LinkOut - more resources