Clines, clusters, and the effect of study design on the inference of human population structure - PubMed (original) (raw)

Clines, clusters, and the effect of study design on the inference of human population structure

Noah A Rosenberg et al. PLoS Genet. 2005 Dec.

Abstract

Previously, we observed that without using prior information about individual sampling locations, a clustering algorithm applied to multilocus genotypes from worldwide human populations produced genetic clusters largely coincident with major geographic regions. It has been argued, however, that the degree of clustering is diminished by use of samples with greater uniformity in geographic distribution, and that the clusters we identified were a consequence of uneven sampling along genetic clines. Expanding our earlier dataset from 377 to 993 markers, we systematically examine the influence of several study design variables--sample size, number of loci, number of clusters, assumptions about correlations in allele frequencies across populations, and the geographic dispersion of the sample--on the "clusteredness" of individuals. With all other variables held constant, geographic dispersion is seen to have comparatively little effect on the degree of clustering. Examination of the relationship between genetic and geographic distance supports a view in which the clusters arise not as an artifact of the sampling scheme, but from small discontinuous jumps in genetic distance for most population pairs on opposite sides of geographic barriers, in comparison with genetic distance for pairs on the same side. Thus, analysis of the 993-locus dataset corroborates our earlier results: if enough markers are used with a sufficiently large worldwide sample, individuals can be partitioned into genetic clusters that match major geographic subdivisions of the globe, with some individuals from intermediate geographic locations having mixed membership in the clusters that correspond to neighboring regions.

PubMed Disclaimer

Conflict of interest statement

Competing interests. The authors have declared that no competing interests exist.

Figures

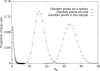
Figure 1

Figure 1. Distribution of the Geographic Dispersion Statistic (An) for Sets of 100 Points Randomly Sampled from a Sphere, Randomly Sampled from the Land Area of the Earth (from among the Points Plotted in Figure 5 of [11]), and Randomly Sampled from the Reported Locations of Individuals in the Dataset

Each distribution is obtained by binning the values of An for 100,000 sets of points.

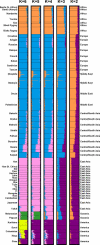
Figure 2

Figure 2. Inferred Population Structure Based on 1,048 Individuals and 993 Markers, Assuming Correlations among Allele Frequencies across Clusters

Each individual is represented by a thin line partitioned into K colored segments that represent the individual's estimated membership fractions in K clusters. Each plot, produced with DISTRUCT [23], is based on the highest-likelihood run of ten runs: the two runs that were used in further analysis, and the eight runs described under “Cluster Analysis using STRUCTURE.” As in [3], four of ten runs with K = 3 separated a cluster corresponding to East Asia instead of one corresponding to Europe, the Middle East, and Central/South Asia. Two of ten runs with K = 5 separated Surui instead of Oceania. The highest-likelihood run of the ten runs with K = 6, shown in the figure, had a different pattern from the other nine runs (not shown). These other runs, instead of subdividing native Americans into two clusters, subdivided a cluster roughly similar to the Kalash cluster seen in [3], except with a less pronounced separation of the Kalash population. The clusteredness scores for the plots shown with K = 2, 3, 4, 5, and 6 are 0.50, 0.76, 0.84, 0.86, and 0.87, respectively.

Figure 3

Figure 3. Mean Clusteredness versus Number of Loci

Each point shows the mean clusteredness of 2,000 runs with the specified sample size and allele frequency correlation model: two replicates for each of ten sets of loci for each of 100 sets of individuals (for 1,048 individuals, it is the mean of 20 runs, as only one set of individuals was used; for 1,048 individuals and 993 loci, it is the mean of two runs, as only one set of loci was used). Error bars denote standard deviations. The _x_-axis is plotted on a logarithmic scale.

Figure 4

Figure 4. Mean Clusteredness versus Geographic Dispersion as Measured by An

Each point shows the mean clusteredness of 20 runs with the specified number of loci and allele frequency correlation model: two replicates for each of ten sets of loci (for 993 loci, it is the mean of two runs, as only one set of loci was used). From left to right, the three groups of points in each plot respectively represent sets of 100, 250, and 500 individuals.

Figure 5

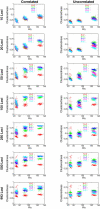
Figure 5. Inferred Population Structure Based on Two Different Sets of 100 Individuals, Using 993 Markers and the Correlated Allele Frequencies Model

The two sets of 100 individuals represent extremes of the distribution of An: the plots on the left are based on a more geographically random sample, and those on the right are based on a less random sample. Each plot is based on the higher-likelihood run among the two runs performed with the given combination of loci and individuals. In all plots, individuals and populations are in the same order as in Figure 2. Black vertical lines at the bottom of the figure separate populations from the different geographic regions described in [3], with the asterisk representing Oceania.

Figure 6

Figure 6. Genetic and Geographic Distance for Pairs of Populations

Red circles indicate comparisons between pairs of populations with majority representation in the same cluster in the K = 5 plot of Figure 2; blue triangles indicate pairs with one population from Eurasia and one from East Asia; brown squares indicate pairs with one population from Africa and the other from Eurasia; and green diamonds indicate pairs with one population from East Asia and the other from either Oceania or America. Comparisons involving one of Hazara, Kalash, and Uygur and other populations from Eurasia or East Asia are marked 1, 2, and 3, respectively. No comparisons are shown between any of these three groups and any African population.

Similar articles

Cited by

References

    1. Bowcock AM, Ruiz-Linares A, Tomfohrde J, Minch E, Kidd JR, et al. High resolution of human evolutionary trees with polymorphic microsatellites. Nature. 1994;368:455–457. - PubMed
    1. Mountain JL, Cavalli-Sforza LL. Multilocus genotypes, a tree of individuals, and human evolutionary history. Am J Hum Genet. 1997;61:705–718. - PMC - PubMed
    1. Rosenberg NA, Pritchard JK, Weber JL, Cann HM, Kidd KK, et al. Genetic structure of human populations. Science. 2002;298:2381–2385. - PubMed
    1. Bamshad MJ, Wooding S, Watkins WS, Ostler CT, Batzer MA, et al. Human population genetic structure and inference of group membership. Am J Hum Genet. 2003;72:578–589. - PMC - PubMed
    1. Tang H, Quertermous T, Rodriguez B, Kardia SLR, Zhu XF, et al. Genetic structure, self-identified race/ethnicity, and confounding in case-control association studies. Am J Hum Genet. 2005;76:268–275. - PMC - PubMed

Publication types

MeSH terms

Grants and funding

LinkOut - more resources