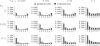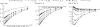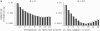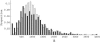Allele frequency distribution under recurrent selective sweeps - PubMed (original) (raw)
Allele frequency distribution under recurrent selective sweeps
Yuseob Kim. Genetics. 2006 Mar.
Abstract
The allele frequency of a neutral variant in a population is pushed either upward or downward by directional selection on a linked beneficial mutation ("selective sweeps"). DNA sequences sampled after the fixation of the beneficial allele thus contain an excess of rare neutral alleles. This study investigates the allele frequency distribution under selective sweep models using analytic approximation and simulation. First, given a single selective sweep at a fixed time, I derive an expression for the sampling probabilities of neutral mutants. This solution can be used to estimate the time of the fixation of a beneficial allele from sequence data. Next, I obtain an approximation to mean allele frequencies under recurrent selective sweeps. Under recurrent sweeps, the frequency spectrum is skewed toward rare alleles. However, the excess of high-frequency derived alleles, previously shown to be a signature of single selective sweeps, disappears with recurrent sweeps. It is shown that, using this approximation and multilocus polymorphism data, genomewide parameters of directional selection can be estimated.
Figures
Figure 1.
Sampling probabilities of neutral mutant alleles after a single selective sweep event (n = 8), for various distances from the selective target and time of the fixation of the beneficial allele. Analytic prediction is obtained from Equation 2. The simulation result is based on 105 coalescent trees for each site. Other parameters: α = 1000, N = 105, θ = 0.01.
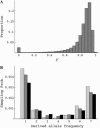
Figure 2.
(A) Distribution of y at the end of a selective sweep. A two-locus forward simulation using the method in K
im
and S
tephan
(2000) was conducted with N = 10,000, s = 0.05, and r/s = 0.025. (B) Sampling probability for n = 8 was determined by transforming an allele frequency x, randomly chosen from distribution φ(x) = θ/x, to y + (1 − y)x with probability x or to (1 − y)x with probability 1 − x. This procedure was repeated 105 times and the resulting distribution of allele frequency was converted to the sampling probability. Columns with light shading are obtained by using a constant y that is the mean of the distribution shown in A [mean = 0.815; (4_Ns_)−r/s = 0.827]. Using variable y in A results in probabilities shown by columns with dark shading. Solid columns represent the results from coalescent simulation (α = 1000, θ = 0.01, r/s = 0.025, and τ = 0).
Figure 3.
Decay of skewed frequency spectrum after a single selective sweep. The expectations of relative heterozygosity (), Tajima's D (given S = 20), and normalized Fay and Wu's H are plotted along the distance from the selective target (given by r/s) for increasing values of τ.
Figure 4.
Allele frequency distribution of neutral mutant alleles under recurrent selective sweeps (n = 15, α = 2000, θ = 0.01, M = 2 × 105, R = 400). Shaded and solid columns show analytic approximation and coalescent simulation, respectively. (A) Probability of sampling i mutant alleles per nucleotide (i = 1, … , n − 1). (B) Frequency spectrum (frequency distribution conditional on polymorphism at the site). Points connected by shaded lines show the frequency spectrum under the standard neutral model [ for i mutants per site].
Figure 4.
Allele frequency distribution of neutral mutant alleles under recurrent selective sweeps (n = 15, α = 2000, θ = 0.01, M = 2 × 105, R = 400). Shaded and solid columns show analytic approximation and coalescent simulation, respectively. (A) Probability of sampling i mutant alleles per nucleotide (i = 1, … , n − 1). (B) Frequency spectrum (frequency distribution conditional on polymorphism at the site). Points connected by shaded lines show the frequency spectrum under the standard neutral model [ for i mutants per site].
Figure 5.
Correlation between Tajima's D and relative reduction of genetic variation under recurrent selective sweeps predicted by analytic approximation. It is assumed that sequence data (n = 25) are taken from a 1-kb segment in the middle of the chromosome and θ = 0.01. The sampling probability given by Equation 4 was transformed to the expected level of variation (), where
, and to expected Tajima's D, using
. Solid curve: α increases from 150 to 5000 with Λ = 4, R = 400. Dashed curves: Λ increases from 1 to 12 with α = 1000 and R = 400, 1000, and 2000. M = 2 × 105.
Figure 6.
Contour plots of composite likelihood (Equation 6) calculated for four random sets of multilocus data (n = 15, L = 30, α = 1000, and 4_N_λ = 4 × 10−5). Contour lines were drawn in increments of five downward from the maximum value (included in the open area).
Figure 7.
Distribution of the maximum composite-likelihood estimate of α when the true value of 4_N_λ = 4 × 10−5 is known. The true value of α is 1000. The likelihood was calculated by varying α from 100 to 5000 in increments of 100. Shaded (solid) columns show the distribution of estimates when the likelihood is based on sampling probabilities (frequency spectrum).
Similar articles
- Soft sweeps III: the signature of positive selection from recurrent mutation.
Pennings PS, Hermisson J. Pennings PS, et al. PLoS Genet. 2006 Dec 15;2(12):e186. doi: 10.1371/journal.pgen.0020186. Epub 2006 Sep 14. PLoS Genet. 2006. PMID: 17173482 Free PMC article. - A Composite-Likelihood Method for Detecting Incomplete Selective Sweep from Population Genomic Data.
Vy HM, Kim Y. Vy HM, et al. Genetics. 2015 Jun;200(2):633-49. doi: 10.1534/genetics.115.175380. Epub 2015 Apr 24. Genetics. 2015. PMID: 25911658 Free PMC article. - Linkage disequilibrium as a signature of selective sweeps.
Kim Y, Nielsen R. Kim Y, et al. Genetics. 2004 Jul;167(3):1513-24. doi: 10.1534/genetics.103.025387. Genetics. 2004. PMID: 15280259 Free PMC article. - Selective Sweeps.
Stephan W. Stephan W. Genetics. 2019 Jan;211(1):5-13. doi: 10.1534/genetics.118.301319. Genetics. 2019. PMID: 30626638 Free PMC article. Review. - Signatures of positive selection: from selective sweeps at individual loci to subtle allele frequency changes in polygenic adaptation.
Stephan W. Stephan W. Mol Ecol. 2016 Jan;25(1):79-88. doi: 10.1111/mec.13288. Epub 2015 Jul 27. Mol Ecol. 2016. PMID: 26108992 Review.
Cited by
- Low nucleotide diversity of the Plasmodium falciparum AP2-EXP2 gene among clinical samples from Ghana.
Quansah E, Zhao J, Eduful KK, Amoako EK, Amenga-Etego L, Halm-Lai F, Luo Q, Shen J, Zhang C, Yu L. Quansah E, et al. Parasit Vectors. 2024 Nov 5;17(1):453. doi: 10.1186/s13071-024-06545-6. Parasit Vectors. 2024. PMID: 39501336 Free PMC article. - Biases in ARG-Based Inference of Historical Population Size in Populations Experiencing Selection.
Marsh JI, Johri P. Marsh JI, et al. Mol Biol Evol. 2024 Jul 3;41(7):msae118. doi: 10.1093/molbev/msae118. Mol Biol Evol. 2024. PMID: 38874402 Free PMC article. - Developing an evolutionary baseline model for humans: jointly inferring purifying selection with population history.
Johri P, Pfeifer SP, Jensen JD. Johri P, et al. bioRxiv [Preprint]. 2023 Apr 11:2023.04.11.536488. doi: 10.1101/2023.04.11.536488. bioRxiv. 2023. PMID: 37090533 Free PMC article. Updated. Preprint. - Sweepstakes reproductive success via pervasive and recurrent selective sweeps.
Árnason E, Koskela J, Halldórsdóttir K, Eldon B. Árnason E, et al. Elife. 2023 Feb 20;12:e80781. doi: 10.7554/eLife.80781. Elife. 2023. PMID: 36806325 Free PMC article. - How Can We Resolve Lewontin's Paradox?
Charlesworth B, Jensen JD. Charlesworth B, et al. Genome Biol Evol. 2022 Jul 2;14(7):evac096. doi: 10.1093/gbe/evac096. Genome Biol Evol. 2022. PMID: 35738021 Free PMC article.
References
- Andolfatto, P., 2001. Adaptive hitchhiking effects on genome variability. Curr. Opin. Genet. Dev. 11: 635–641. - PubMed
- Bachtrog, D., 2004. Evidence that positive selection drives Y-chromosome degeneration in Drosophila miranda. Nat. Genet. 36: 518–522. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources