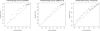A fast and flexible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase - PubMed (original) (raw)

A fast and flexible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase

Paul Scheet et al. Am J Hum Genet. 2006 Apr.

Abstract

We present a statistical model for patterns of genetic variation in samples of unrelated individuals from natural populations. This model is based on the idea that, over short regions, haplotypes in a population tend to cluster into groups of similar haplotypes. To capture the fact that, because of recombination, this clustering tends to be local in nature, our model allows cluster memberships to change continuously along the chromosome according to a hidden Markov model. This approach is flexible, allowing for both "block-like" patterns of linkage disequilibrium (LD) and gradual decline in LD with distance. The resulting model is also fast and, as a result, is practicable for large data sets (e.g., thousands of individuals typed at hundreds of thousands of markers). We illustrate the utility of the model by applying it to dense single-nucleotide-polymorphism genotype data for the tasks of imputing missing genotypes and estimating haplotypic phase. For imputing missing genotypes, methods based on this model are as accurate or more accurate than existing methods. For haplotype estimation, the point estimates are slightly less accurate than those from the best existing methods (e.g., for unrelated Centre d'Etude du Polymorphisme Humain individuals from the HapMap project, switch error was 0.055 for our method vs. 0.051 for PHASE) but require a small fraction of the computational cost. In addition, we demonstrate that the model accurately reflects uncertainty in its estimates, in that probabilities computed using the model are approximately well calibrated. The methods described in this article are implemented in a software package, fastPHASE, which is available from the Stephens Lab Web site.

PubMed Disclaimer

Figures

Figure 1

Figure 1

Illustration of how our model allows cluster membership to change continuously along a chromosome. Each column represents a SNP, with the two alleles indicated by open and crossed squares. Successive pairs of rows represent the estimated pair of haplotypes for successive individuals. Colors represent estimated cluster membership of each allele, which changes as one moves along each haplotype. Locally, each cluster can be thought of as representing a (common) combination of alleles at tightly linked SNPs, and the figure illustrates how each haplotype is modeled as a mosaic of these common combinations. The figure was produced by fitting our model to the HapMap data from 60 unrelated CEPH individuals (see the “Results” section) and then taking a single sample of cluster memberships and haplotypes from their conditional distribution, given the genotype data and parameter estimates (appendix B). For brevity, haplotypes from only 10 individuals are shown.

Figure 2

Figure 2

Calibration of our model for predicting uncertainty in inferred genotypes and haplotypes. Points (triangles) represent probabilities obtained by averaging over the 20 runs of the EM algorithm, as described in the text.

Similar articles

Cited by

References

Web Resources

    1. GERBIL, http://www.cs.tau.ac.il/~rshamir/gerbil/
    1. HAP Web site, http://research.calit2.net/hap/
    1. HaploBlock, http://bioinfo.cs.technion.ac.il/haploblock/
    1. International HapMap Project, http://www.hapmap.org/
    1. SeattleSNPs, http://pga.gs.washington.edu

References

    1. Akaike H (1974) A new look at the statistical model identification. IEEE Trans Automatic Control AC 19:719–723
    1. Bates JM, Granger CWJ (1969) The combination of forecasts. Oper Res Q 20:451–468
    1. Breiman L (1996) Bagging predictors. Mach Learn 24:123–140
    1. Chapman J, Cooper J, Todd J, Clayton D (2003) Detecting disease associations due to linkage disequilibrium using haplotype tags: a class of tests and the determinants of statistical power. Hum Hered 56:18–3110.1159/000073729 - DOI - PubMed
    1. Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B 39:1–38

Publication types

MeSH terms

LinkOut - more resources