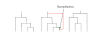Fast "coalescent" simulation - PubMed (original) (raw)
Fast "coalescent" simulation
Paul Marjoram et al. BMC Genet. 2006.
Abstract
Background: The amount of genome-wide molecular data is increasing rapidly, as is interest in developing methods appropriate for such data. There is a consequent increasing need for methods that are able to efficiently simulate such data. In this paper we implement the sequentially Markovian coalescent algorithm described by McVean and Cardin and present a further modification to that algorithm which slightly improves the closeness of the approximation to the full coalescent model. The algorithm ignores a class of recombination events known to affect the behavior of the genealogy of the sample, but which do not appear to affect the behavior of generated samples to any substantial degree.
Results: We show that our software is able to simulate large chromosomal regions, such as those appropriate in a consideration of genome-wide data, in a way that is several orders of magnitude faster than existing coalescent algorithms.
Conclusion: This algorithm provides a useful resource for those needing to simulate large quantities of data for chromosomal-length regions using an approach that is much more efficient than traditional coalescent models.
Figures
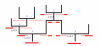
Figure 1
The various categories of recombination. Illustration of the different types of recombinations. Ancestral material is shown as solid red lines, while non-ancestral material is shown as red-dotted lines. Locations of recombinations are shown below and to the left of the recombination event. Type of recombination is indicated with a blue numeral above the event.
Figure 2
Illustration of FastCoal algorithm. This figure shows how the algorithm forms the next tree along the chromosome, moving from left-to-right, given the state of the current tree.
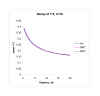
Figure 3
Decay of _r_2. This figure shows how _r_2 decays as a function of distance for both the SMC and SMC' algorithm and for an exact coalescent model (simulated using ms). Data was simulated for a 2 Mb region and a sample size of n = 20.
Similar articles
- A sequential coalescent algorithm for chromosomal inversions.
Peischl S, Koch E, Guerrero RF, Kirkpatrick M. Peischl S, et al. Heredity (Edinb). 2013 Sep;111(3):200-9. doi: 10.1038/hdy.2013.38. Epub 2013 May 1. Heredity (Edinb). 2013. PMID: 23632894 Free PMC article. - Critical assessment of coalescent simulators in modeling recombination hotspots in genomic sequences.
Yang T, Deng HW, Niu T. Yang T, et al. BMC Bioinformatics. 2014 Jan 3;15:3. doi: 10.1186/1471-2105-15-3. BMC Bioinformatics. 2014. PMID: 24387001 Free PMC article. - The Bacterial Sequential Markov Coalescent.
De Maio N, Wilson DJ. De Maio N, et al. Genetics. 2017 May;206(1):333-343. doi: 10.1534/genetics.116.198796. Epub 2017 Mar 3. Genetics. 2017. PMID: 28258183 Free PMC article. - Linkage disequilibrium: what history has to tell us.
Nordborg M, Tavaré S. Nordborg M, et al. Trends Genet. 2002 Feb;18(2):83-90. doi: 10.1016/s0168-9525(02)02557-x. Trends Genet. 2002. PMID: 11818140 Review. - Mapping genes through the use of linkage disequilibrium generated by genetic drift: 'drift mapping' in small populations with no demographic expansion.
Terwilliger JD, Zöllner S, Laan M, Pääbo S. Terwilliger JD, et al. Hum Hered. 1998 May-Jun;48(3):138-54. doi: 10.1159/000022794. Hum Hered. 1998. PMID: 9618061 Review.
Cited by
- On the Distribution of Tract Lengths During Adaptive Introgression.
Shchur V, Svedberg J, Medina P, Corbett-Detig R, Nielsen R. Shchur V, et al. G3 (Bethesda). 2020 Oct 5;10(10):3663-3673. doi: 10.1534/g3.120.401616. G3 (Bethesda). 2020. PMID: 32763953 Free PMC article. - Robust inference of population size histories from genomic sequencing data.
Upadhya G, Steinrücken M. Upadhya G, et al. PLoS Comput Biol. 2022 Sep 16;18(9):e1010419. doi: 10.1371/journal.pcbi.1010419. eCollection 2022 Sep. PLoS Comput Biol. 2022. PMID: 36112715 Free PMC article. - Rapidly Registering Identity-by-Descent Across Ancestral Recombination Graphs.
Yang S, Carmi S, Pe'er I. Yang S, et al. J Comput Biol. 2016 Jun;23(6):495-507. doi: 10.1089/cmb.2016.0016. Epub 2016 Apr 22. J Comput Biol. 2016. PMID: 27104872 Free PMC article. - A principled approach to deriving approximate conditional sampling distributions in population genetics models with recombination.
Paul JS, Song YS. Paul JS, et al. Genetics. 2010 Sep;186(1):321-38. doi: 10.1534/genetics.110.117986. Epub 2010 Jun 30. Genetics. 2010. PMID: 20592264 Free PMC article. - Forward-time simulation of realistic samples for genome-wide association studies.
Peng B, Amos CI. Peng B, et al. BMC Bioinformatics. 2010 Sep 1;11:442. doi: 10.1186/1471-2105-11-442. BMC Bioinformatics. 2010. PMID: 20809983 Free PMC article.
References
- Kingman JFC. On the genealogy of large populations. J Appl Prob. 1982;19A:27–43.
- Jiang R, Marjoram P, Stram D. "New data from old" – simulation of test data for mapping studies. 2005.
Publication types
MeSH terms
Grants and funding
- P50 HG002790/HG/NHGRI NIH HHS/United States
- R01 GM069890/GM/NIGMS NIH HHS/United States
- GM069890-01A1/GM/NIGMS NIH HHS/United States
- HG002790-01A1/HG/NHGRI NIH HHS/United States
LinkOut - more resources
Full Text Sources