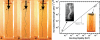Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement - PubMed (original) (raw)

Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement

Clifford P Brangwynne et al. J Cell Biol. 2006.

Abstract

Cytoskeletal microtubules have been proposed to influence cell shape and mechanics based on their ability to resist large-scale compressive forces exerted by the surrounding contractile cytoskeleton. Consistent with this, cytoplasmic microtubules are often highly curved and appear buckled because of compressive loads. However, the results of in vitro studies suggest that microtubules should buckle at much larger length scales, withstanding only exceedingly small compressive forces. This discrepancy calls into question the structural role of microtubules, and highlights our lack of quantitative knowledge of the magnitude of the forces they experience and can withstand in living cells. We show that intracellular microtubules do bear large-scale compressive loads from a variety of physiological forces, but their buckling wavelength is reduced significantly because of mechanical coupling to the surrounding elastic cytoskeleton. We quantitatively explain this behavior, and show that this coupling dramatically increases the compressive forces that microtubules can sustain, suggesting they can make a more significant structural contribution to the mechanical behavior of the cell than previously thought possible.

PubMed Disclaimer

Figures

Figure 1.

Figure 1.

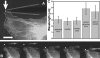
Structural dynamics of fluorescently labeled microtubules in living cells. (A) Fluorescence micrograph of a Cos7 cell expressing EGFP-labeled microtubules that frequently display sinusoidal shapes (arrowheads) at their ends, which is where they hit end-on at the cell periphery (white line indicates cell periphery). (B) Time sequence (left to right; 5 s between images) showing one microtubule from A at higher magnification as it buckles into a sinusoidal shape when it hits the cell edge (Video 1). Bar, 5 μm. Video 1 is available at

http://www.jcb.org/cgi/content/full/jcb.200601060/DC1

.

Figure 2.

Figure 2.

Deformation response of initially straight microtubules compressively loaded by a microneedle. (A) To determine if microtubules in cells buckle into short-wavelength shapes when artificially compressed by an exogenous force, we used a fine glass microneedle to push on initially straight microtubules at the cell periphery (white dot, needle tip position; gray lines, needle outline) Bar, 10 μm. (B) Time sequence of the microtubule in A compressed by the needle as it is moved from top to bottom (left to right; 1.1 s between images; Video 3). The microtubule buckles into a sinusoidal shape similar to that of naturally buckling microtubules. (C) The wavelength of microtubules buckled by the needle is the same as that of microtubules buckled as they polymerize into the cell cortex and that of microtubule buckling caused by actomyosin contractility in beating cardiac myocytes. When the actin cytoskeleton was disrupted in Cos7 cells treated with cytochalasin D, the wavelength of both naturally buckled and needle-buckled microtubules increased. MTs, microtubules. Error bars are ± SD. Video 3 is available at

http://www.jcb.org/cgi/content/full/jcb.200601060/DC1

.

Figure 3.

Figure 3.

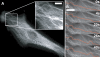
Microtubule buckling caused by cell contractility. (A) Fluorescence micrograph of a capillary cell expressing EGFP-tubulin and low and high (inset) magnification showing that microtubule buckling occurs throughout the cytoplasm with similar short-wavelength forms as observed at the periphery. (B) Time sequence of a movie of the cell shown in A, with a single microtubule highlighted in orange for clarity, demonstrated that high curvature buckling occurs in localized regions separated by straight regions of the same microtubule. Bars, 5 μm. Video 8. Video 8 is available at

http://www.jcb.org/cgi/content/full/jcb.200601060/DC1

.

Figure 4.

Figure 4.

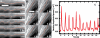
Periodic microtubule buckling caused by contractile beating of heart cells. (A) Time sequence of a microtubule buckling in a beating cardiac myocyte. The microtubule can be seen to buckle and unbuckle successively three times (Video 5). (B) Time sequence of a microtubule buckling and unbuckling in a beating cardiac myocyte, while neighboring microtubules remain straight. The microtubule buckles in a specific spot in each of the successive buckling events (Video 6). (C) Fourier mode analysis of the microtubule shown in B demonstrates that the amplitude of the bending on wavelengths of ∼3 μm shows periodic spikes caused by periodic buckling of the microtubule under successive contractile beats. The amplitude of this periodic buckling decreases with time as the intensity of the contractile force decreases with time because of photodamage. Bars, 3 μm. Videos 5 and 6 are available at

http://www.jcb.org/cgi/content/full/jcb.200601060/DC1

.

Figure 5.

Figure 5.

Macroscopic buckling with a plastic rod. (A) When a thin (∼0.2-mm-diam) plastic rod was compressed in a 1-cm-wide rectangular chamber filled with water it underwent classic long-wavelength Euler buckling. (B) When this experiment was repeated with a rod embedded in an elastic gelatin network, short wavelength buckling (λ = 1.1 cm) was observed. (C) A local region of the gelatin network was first disrupted by overcompression of the rod. When the rod was subsequently released and then compressed again, local short-wavelength buckling was limited to this same disrupted region, even while the rest of the rod remained straight. (D) When this experiment was repeated with plastic rods of differing stiffness, there was good agreement with theory in all cases (top right data points). The data from microtubules buckled because of exogenous forces, polymerization forces, and actomyosin contractile forces also show good agreement with this theory (bottom left data points). Vertical error bars are ± SD. Horizontal error bars (bottom left cell MT data) are an estimate of the uncertainty in MT bending rigidity.

Figure 6.

Figure 6.

Decay of transmission of the compressive force. (A) In microtubules compressed by force application at their tips (Figs. 1 and 2), the buckling amplitude decays along the length of the microtubule, reflecting an attenuation of the compressive force by the surrounding network. (B) Similar behavior was seen in the macroscopic experiments using plastic rods embedded in elastic gelatin.

Figure 7.

Figure 7.

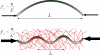
Schematic summarizing how the presence of the surrounding elastic cytoskeleton reinforces microtubules in living cells. Free microtubules in vitro buckle on the large length scale of the filament, at a small critical buckling force. Microtubules in living cells are surrounded by a reinforcing cytoskeleton. This leads to a larger critical force, and buckling on a short wavelength.

Similar articles

Cited by

References

    1. Aist, J.R., and C.J. Bayles. 1991. Detection of spindle pushing forces in vivo during anaphase b in the fungus Nectria haematococca. Cell Motil. Cytoskeleton. 19:18–24.
    1. Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2005. Molecular Biology of the Cell. Fourth edition. Garland Science, New York. 1463 pp.
    1. Bloom, G.S., F.C. Luca, and R.B. Vallee. 1985. Cross-linking of intermediate filaments to microtubules by microtubule-associated protein 2. Ann. N. Y. Acad. Sci. 455:18–31. - PubMed
    1. Brodland, G.W., and R. Gordon. 1990. Intermediate filaments may prevent buckling of compressively loaded microtubules. J. Biomech. Eng. 112:319–321. - PubMed
    1. Burnside, B. 1971. Microtubules and microfilaments in newt neuralation. Dev. Biol. 26:416–441. - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources