Population genetics models of competition between transposable element subfamilies - PubMed (original) (raw)
Population genetics models of competition between transposable element subfamilies
Arnaud Le Rouzic et al. Genetics. 2006 Oct.
Abstract
Transposable elements are one of the major components of genomes. Some copies are fully efficient; i.e., they are able to produce the proteins needed for their own transposition, and they can move and duplicate into the genome. Other copies are mutated. They may have lost their moving ability, their coding capacity, or both, thus becoming pseudogenes slowly eliminated from the genome through deletions and natural selection. Little is known about the dynamics of such mutant elements, particularly concerning their interactions with autonomous copies. To get a better understanding of the transposable elements' evolution after their initial invasion, we have designed a population genetics model of transposable elements dynamics including mutants or nonfunctional sequences. We have particularly focused on the case where these sequences are nonautonomous elements, known to be able to use the transposition machinery produced by the autonomous ones. The results show that such copies generally prevent the system from achieving a stable transposition-selection equilibrium and that nonautonomous elements can invade the system at the expense of autonomous ones. The resulting dynamics are mainly cyclic, which highlights the similarities existing between genomic selfish DNA sequences and host-parasite systems.
Figures
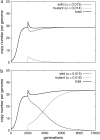
Figure 1.—
Determinist dynamics of a mobility mutant. A functional element (u = 0.015, v = 0.001, a = 1, s = −0.01) is introduced at the first generation with an average of 1 copy per individual. After 2000 generations, when the copy number is stabilized (transposition–selection equilibrium), a mutant copy with the same features except for u is introduced (five copies in all individuals, to make the plots more easily readable). (a) If the mobility of the mutant is lower than that of the wild element (u = 0.014), the mutant will be eliminated. (b) If the mutant has a better mobility (u = 0.016), it will progressively invade the population.
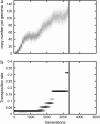
Figure 2.—
Evolution of the genomic copy number (a) and the transposition rate (b) in a stochastic simulation. One thousand TEs (u = 0.02, s = −0.01, v = 0.001) are introduced in a population of size N = 1000. The transposition rate u can mutate in both directions with the rate μ_u_ = 10−4 and the amplitude δ_u_ = 0.1 (see
materials and methods
). The shaded level is proportional to the distribution frequency of the copy number (a) and of the transposition rate (b). Only higher-rate mutants are conserved and replace the former TE after a short polymorphic stage, and the average transposition rate thus grows regularly, shifting the transposition–selection equilibrium toward a higher copy number. When the copy number per genome becomes too high, the whole population could disappear (vertical solid line).
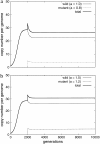
Figure 3.—
Determinist dynamics of an activity mutant. Whatever the activity of the mutant—(a) lower, a = 0.8, or (b) higher, a = 1.2—both mutant and wild elements will coexist in the genome. All the parameters are the same as those in Figure 1, except activity.
Figure 4.—
Dynamics of TE autonomous copies and their corresponding nonautonomous mutants. Populations are initialized with an average of one autonomous copy per individual. The columns represent, respectively, (i) the evolution of the average total copy number per genome (i.e., autonomous plus nonautonomous) in a single simulation (N = 200 individuals), (ii) the same with N = 2000 individuals, (iii) the evolution of the average copy number for autonomous and nonautonomous copies in the same simulations as those in column ii (initial state is 1 autonomous and 0 nonautonomous), and (iv) the same dynamics predicted by the determinist model. Each line represents a different parameter set. (a) s = −0.01, u = 0.02, v = 0.001, μ_a_ = 0; (b) s = −0.005, u = 0.02, v = 0.001, μ_a_ = 0.0005; (c) s = −0.005, u = 0.02, v = 0.001, μ_a_ = 0.005; (d) s = −0.005, u = 0.015, v = 0.001, μ_a_ = 0.001. In a, there is no mutation and the dynamics correspond to the invasion of a single, active element.
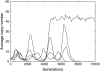
Figure 5.—
Examples of simulations of the evolution of the total genomic copy number when there are no mutations between autonomous and nonautonomous forms. Five repetitions with the same initial state are plotted. Initially, 1000 autonomous and 1000 nonautonomous elements are present in the genome of the N = 1000 individuals of the population. The nonautonomous copy (a = 0, u = 0.02, v = 0.001, s = −0.005) is less deleterious than the active copy (a = 1, s = −0.01). If the nonautonomous element is lost, the copy number stabilizes to the expected transposition–selection equilibrium (one simulation among five). If the autonomous copy is lost, there is no more transposition, and all copies are finally lost.
Similar articles
- Maintenance of long-term transposable element activity through regulation by nonautonomous elements.
Omole AD, Czuppon P. Omole AD, et al. Genetics. 2025 Feb 5;229(2):iyae209. doi: 10.1093/genetics/iyae209. Genetics. 2025. PMID: 39810601 - Nonautonomous transposable elements in prokaryotes and eukaryotes.
Hartl DL, Lozovskaya ER, Lawrence JG. Hartl DL, et al. Genetica. 1992;86(1-3):47-53. doi: 10.1007/BF00133710. Genetica. 1992. PMID: 1334917 Review. - A population genetics theory for piRNA-regulated transposable elements.
Tomar SS, Hua-Van A, Le Rouzic A. Tomar SS, et al. Theor Popul Biol. 2023 Apr;150:1-13. doi: 10.1016/j.tpb.2023.02.001. Epub 2023 Mar 1. Theor Popul Biol. 2023. PMID: 36863578 - Long-term evolution of transposable elements.
Le Rouzic A, Boutin TS, Capy P. Le Rouzic A, et al. Proc Natl Acad Sci U S A. 2007 Dec 4;104(49):19375-80. doi: 10.1073/pnas.0705238104. Epub 2007 Nov 26. Proc Natl Acad Sci U S A. 2007. PMID: 18040048 Free PMC article. - Models of the population genetics of transposable elements.
Le Rouzic A, Deceliere G. Le Rouzic A, et al. Genet Res. 2005 Jun;85(3):171-81. doi: 10.1017/S0016672305007585. Genet Res. 2005. PMID: 16174335 Review.
Cited by
- Genomic landscape and evolutionary dynamics of mariner transposable elements within the Drosophila genus.
Wallau GL, Capy P, Loreto E, Hua-Van A. Wallau GL, et al. BMC Genomics. 2014 Aug 27;15(1):727. doi: 10.1186/1471-2164-15-727. BMC Genomics. 2014. PMID: 25163909 Free PMC article. - Pragmatic turn in biology: From biological molecules to genetic content operators.
Witzany G. Witzany G. World J Biol Chem. 2014 Aug 26;5(3):279-85. doi: 10.4331/wjbc.v5.i3.279. World J Biol Chem. 2014. PMID: 25225596 Free PMC article. Review. - Experimental evolution reveals hyperparasitic interactions among transposable elements.
Robillard É, Le Rouzic A, Zhang Z, Capy P, Hua-Van A. Robillard É, et al. Proc Natl Acad Sci U S A. 2016 Dec 20;113(51):14763-14768. doi: 10.1073/pnas.1524143113. Epub 2016 Dec 5. Proc Natl Acad Sci U S A. 2016. PMID: 27930288 Free PMC article. - Genome-wide analysis of intraspecific transposon diversity in yeast.
Bleykasten-Grosshans C, Friedrich A, Schacherer J. Bleykasten-Grosshans C, et al. BMC Genomics. 2013 Jun 14;14:399. doi: 10.1186/1471-2164-14-399. BMC Genomics. 2013. PMID: 23768249 Free PMC article. - Horizontal transposon transfer in eukarya: detection, bias, and perspectives.
Wallau GL, Ortiz MF, Loreto EL. Wallau GL, et al. Genome Biol Evol. 2012;4(8):689-99. doi: 10.1093/gbe/evs055. Epub 2012 Jul 12. Genome Biol Evol. 2012. PMID: 22798449 Free PMC article. Review.
References
- Adams, M. D., S. E. Celniker, R. A. Holt, C. A. Evans, J. D. Gocayne et al., 2000. The genome sequence of Drosophila melanogaster. Science 287: 1185–1195. - PubMed
- Anxolabéhère, D., M. G. Kidwell and G. Periquet, 1988. Molecular characteristics of diverse populations are consistent with the hypothesis of a recent invasion of Drosophila melanogaster by mobile P elements. Mol. Biol. Evol. 5: 252–269. - PubMed
- Augé-Gouillou, C., M. Hamelin, M. Demattei, M. Periquet and Y. Bigot, 2001. The wild-type conformation of the Mos-1 inverted terminal repeats is suboptimal for transposition in bacteria. Mol. Genet. Genomics 265: 51–57. - PubMed
- Bartolomé, C., X. Maside and B. Charlesworth, 2002. On the abundance and distribution of transposable elements in the genome of Drosophila melanogaster. Mol. Biol. Evol. 19: 926–937. - PubMed
- Bascompte, J., and F. Rodriguez-Trelles, 1998. Eradication thresholds in epidemiology, conservation biology and genetics. J. Theor. Biol. 192: 415–418. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources