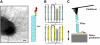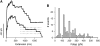The mechanical properties of E. coli type 1 pili measured by atomic force microscopy techniques - PubMed (original) (raw)

The mechanical properties of E. coli type 1 pili measured by atomic force microscopy techniques

Eric Miller et al. Biophys J. 2006.

Abstract

The first step in the encounter between a host and a pathogen is attachment to the host epithelium. For uropathogenic Escherichia coli, these interactions are mediated by type 1 and P adhesive pili, which are long (approximately 1 microm) rods composed of more than 1000 protein subunits arranged in a helical structure. Here we used single-molecule atomic force microscopy to study the mechanical properties of type 1 pili. We found that type 1 pili readily extend under an applied force and that this extensibility is the result of unwinding the pilus rod's helical quaternary structure. The forced unraveling is also reversible, with helical rewinding taking place under considerable forces (approximately 60 pN). These data are similar to those obtained on P pili using optical tweezers, indicating that these are conserved properties of uropathogenic E. coli pili. We also show that our data can readily be reproduced using Monte Carlo simulation techniques based on a two-state kinetic model. This model provides a simple way to extrapolate the mechanical behavior of pili under a wide range of forces. We propose that type 1 pilus unraveling is an essential mechanism for absorbing physiological shear forces encountered during urinary tract infections and probably essential for adhesion and colonization of the bladder epithelium.

PubMed Disclaimer

Figures

FIGURE 1

FIGURE 1

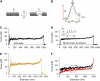
(A, left) Negative-stain electron micrograph of uropathogenic E. coli (UTI89) cell expressing type 1 pili (scale bar = 200 nm). (A, right) A cartoon diagram showing the structural subunits of type 1 pili. FimH is the adhesin at the distal end of the tip fibrillum, followed by FimG and FimF. Oligos of FimA form the helical pilus rod structure that is visible in the micrograph. (B) Two-dimensional diagram of donor-strand exchange between FimA Ig-like domains. Each pilin structural subunit donates its _N_-terminal extension to complete its neighbor's fold and form a protein chain. The _N_-terminal extension is held in place through noncovalent interactions (shaded region) such as hydrogen bonds and hydrophobic interactions. Each pilin subunit has one disulfide bond (red) between the A and B _β_-strands, close to where the _N_-terminal extension ends. (C) Diagram of the single-molecule AFM. Purified pili were adsorbed onto a glass substrate and then stretched using the tip of a cantilever (see Materials and Methods).

FIGURE 2

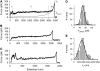
FIGURE 2

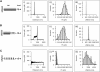
Force-extension curves obtained after stretching type 1 pili. (A–C) Examples of force-extension curves for type 1 pili. There are three distinct regions of pili stretching, which are marked by the vertical dotted lines (I, II, and III). The first region represents nonspecific interactions between the AFM tip and sample. The second region is a force plateau, _F_plateau (dashed line) that corresponds to the unwinding of the pilus rod at a constant force. The third region is the final stretching of the completely unraveled pilus rod. The continuous line shows the prediction of the WLC equation using a persistence length, p, of 1.2 nm. (D and E) Frequency histograms for the plateau force, _F_plateau, and contour length, _L_c. Gaussian fits gave a mean _F_plateau of ∼60 pN (63 ± 17 pN, n = 564, 94 different pili) and _L_c ≈ 2 _μ_m (1.9 ± 0.7 _μ_m, n = 230).

FIGURE 3

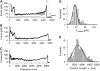
FIGURE 3

Force-extension patterns for P pili. (A–C) Examples of force-extension curves for several P pili. (A) Solid line shows the prediction of the WLC equation using a persistence length, p, of 1.6 nm. (D and E) Frequency histograms for the plateau force, _F_plateau, and contour length, _L_c. The lines correspond to Gaussian fits, which gave mean _F_plateau of ∼35 pN (34 ± 14 pN, n = 246, 48 different pili) and _L_c ≈ 3 _μ_m (2.9 ± 1.8 _μ_m, n = 130).

FIGURE 4

FIGURE 4

The forced unraveling of the helical rod structure is fully reversible. Consecutive force-extension and relaxation curves for a single type 1 pilus using a double-pulse stretching protocol (i–iii) in which the pilus was first extended (black traces) and then relaxed (gray traces). The time delay between stretching pulses was 10 s. The second extension-relaxation cycle (ii) starts at ∼90 nm away from the coverslip to prevent picking up more pili. The third trace (iii) corresponds to the spontaneous detachment of the pilus from the AFM tip.

FIGURE 5

FIGURE 5

Simultaneous stretching of multiple type 1 pili. (A) To promote numerous pili binding to the cantilever, a large concentration of type 1 pili was allowed to adsorb to the coverslips. Force-extension curves show a stair-step pattern, corresponding to the stretching and detachment of multiple pili. The number of pili being stretched was estimated by counting the number of back steps in the force-extension curves. (B) Frequency histogram for the force between steps, _F_step (dotted lines in bottom trace), reveals a multimodal force detachment pattern. The mean peaks are at found at 50, 112, 192, 272, 336, and 400 pN (n = 130 steps) with a mean _F_step of 69 pN.

FIGURE 6

FIGURE 6

Monte Carlo simulation of type 1 pili elasticity. (A) A simple model for the reversible unwinding of the pili helical rod under a stretching force. This model divides the helical rod into small folded segments of contour length _l_F that can undergo an all-or-none transition into a stretched, unwound state of contour length _l_U. The increase in contour length on unwinding of a turn is Δ_L_c = _l_U − _l_F, where _l_F ≈ 3 nm and _l_U ≈ 8 nm. (B) The unraveling of the helical rod was modeled as a two-state Markovian process in which the rate constants for unwinding, α, and rewinding, β, are force dependent and are given by α = _α_0exp(_F_Δ_x_u/kT) and β = _β_oexp(−_F_Δ_x_f/kT), where F is the applied force, Δ_x_u and Δ_x_f are the unwinding and rewinding distances, and _α_0 and _β_0 are the rate constants at zero force. (C) Experimental force-extension curve for a type 1 pilus. (D) Monte Carlo simulation of a force-extension curve obtained by stretching, at a constant speed (1 nm/ms), 245 subunits. The kinetic parameters are: _α_o = 5 × 10−2 s−1; _β_o = 7 × 102 s−1; Δ_x_u= 0.2 nm; and Δ_x_f = 0.5 nm. (E) Superimposition of the experimental trace (orange) and the simulated trace (green). (F) Monte Carlo simulation of force-extension (black trace) and force-relaxation (red trace) curves obtained by stretching/relaxing 320 subunits, using the same kinetic parameters as in panel D.

FIGURE 7

FIGURE 7

Effect of pili elastic properties on bond lifetime. (A–C) Monte Carlo simulations of the effect of pili mechanical properties on the lifetime of the receptor bonds under a stretching force. (A) Simulation of a bond linked to a rigid rod made of 500 nonextensible turns in which each turn can extend by only Δ_L_c = 0.05 nm. The bond survives for 0.5 ± 0.3 s (iii) and breaks at 611 ± 148 pN, n = 170 (ii). (B) Simulation of a bond linked to a semirigid rod made of 400 nonextensible (Δ_L_c = 0.05 nm) plus 100 extensible (Δ_L_c = 5 nm) turns. The bond survives for 0.9 ± 0.3 s (iii) and breaks at 455 ± 231 pN, n = 172 (ii). (C) Simulation of a bond linked to an extensible rod made of 500 turns in which the unwinding of each turn leads to an increase in contour length, Δ_L_c = 5 nm. The bond survives for 1.9 ± 1.0 s (iii) and breaks at 62 ± 19 pN, n = 176 (ii).

Similar articles

Cited by

References

    1. Langermann, S., S. Palaszynski, M. Barnhart, G. Auguste, J. S. Pinkner, J. Burlein, P. Barren, S. Koenig, S. Leath, et al. 1997. Prevention of mucosal Escherichia coli infection by FimH-adhesin-based systemic vaccination. Science. 276:607–611. - PubMed
    1. Bullitt, E., and L. Makowski. 1998. Bacterial adhesion pili are heterologous assemblies of similar subunits. Biophys. J. 74:623–632. - PMC - PubMed
    1. Gong, M., and L. Makowski. 1992. Helical structure of P pili from Escherichia coli. Evidence from x-ray fiber diffraction and scanning transmission electron microscopy. J. Mol. Biol. 228:735–742. - PubMed
    1. Soto, G. E., and S. J. Hultgren. 1999. Bacterial adhesins: common themes and variations in architecture and assembly. J. Bacteriol. 181:1059–1071. - PMC - PubMed
    1. Jones, C. H., J. S. Pinkner, R. Roth, J. Heuser, A. V. Nicholes, S. N. Abraham, and S. J. Hultgren. 1995. FimH adhesin of type 1 pili is assembled into a fibrillar tip structure in the Enterobacteriaceae. Proc. Natl. Acad. Sci. USA. 92:2081–2085. - PMC - PubMed

Publication types

MeSH terms

Grants and funding

LinkOut - more resources