Statistical tests for detecting positive selection by utilizing high-frequency variants - PubMed (original) (raw)

Statistical tests for detecting positive selection by utilizing high-frequency variants

Kai Zeng et al. Genetics. 2006 Nov.

Abstract

By comparing the low-, intermediate-, and high-frequency parts of the frequency spectrum, we gain information on the evolutionary forces that influence the pattern of polymorphism in population samples. We emphasize the high-frequency variants on which positive selection and negative (background) selection exhibit different effects. We propose a new estimator of theta (the product of effective population size and neutral mutation rate), thetaL, which is sensitive to the changes in high-frequency variants. The new thetaL allows us to revise Fay and Wu's H-test by normalization. To complement the existing statistics (the H-test and Tajima's D-test), we propose a new test, E, which relies on the difference between thetaL and Watterson's thetaW. We show that this test is most powerful in detecting the recovery phase after the loss of genetic diversity, which includes the postselective sweep phase. The sensitivities of these tests to (or robustness against) background selection and demographic changes are also considered. Overall, D and H in combination can be most effective in detecting positive selection while being insensitive to other perturbations. We thus propose a joint test, referred to as the DH test. Simulations indicate that DH is indeed sensitive primarily to directional selection and no other driving forces.

PubMed Disclaimer

Figures

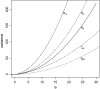
F<sc>igure</sc> 1.—

Figure 1.—

Variance of the five estimators of θ. Sample size (n) is 50.

F<sc>igure</sc> 2.—

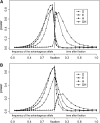
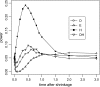
Figure 2.—

(A) Changes in formula image at the linked neutral locus as the advantageous mutation increases in frequency (f). (B) Changes in R(i) at different times τ (measured in units of 4_N_ generations) after fixation of the advantageous mutation. In all simulations, the parameters are defined as follows: θ = 4_N_μ, where μ is the mutation rate for the linked neutral locus; s is the selective coefficient of the advantageous mutation and c is the recombination distance (between the neutral variation under investigation and the advantageous mutation nearby), which is usually scaled by the selective coefficient. The parameter values are θ = 5, s = 0.001, c/s = 0.02, and sample size (n) is 50. In the simulation for hitchhiking, we also incorporated intragenic recombination among the neutral variants under investigation. The intragenic recombination rate of the neutral locus, multiplied by 4_N_, is 25 here and in Figure 3. The values of θ and intragenic recombination rate were chosen to reflect the reality of D. melanogaster; i.e., the scaled local recombination rate is about fivefold as large as the local population mutation rate. Intragenic recombination in other cases has a negligible effect on the results and was not incorporated.

F<sc>igure</sc> 3.—

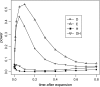
Figure 3.—

Power of the tests before and after hitchhiking is completed. The x_-axis on the left represents the increase in the frequency of the advantageous mutation; on the right is the time after fixation (measured in units of 4_N generations). All parameter values are the same as those of Figure 2. All tests were one-sided; values falling into the lower 5% tail of the null distribution were considered significant. Results shown in Figures 4–6 were produced by the same method. (A) c/s = formula image; (B) c/s = 0.02.

F<sc>igure</sc> 4.—

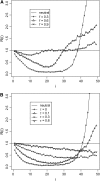
Figure 4.—

Sensitivity (or power) of the tests to population expansion. We assume that the effective population size increases 10-fold instantaneously at time 0 to θ = 5. Sample size (n) is 50. Time is measured in units of 4_N_ generations.

F<sc>igure</sc> 5.—

Figure 5.—

Sensitivity (or power) of the tests to population shrinkage. We assume that the effective population size decreases 10-fold instantaneously at time 0 to θ = 2. Sample size (n) is 50. Time is measured in units of 4_N_ generations.

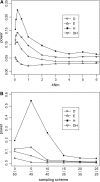
F<sc>igure</sc> 6.—

Figure 6.—

Sensitivity (or power) of the tests to population subdivision. A symmetric two-deme model with θ = 2 per deme (2_N_ genes per deme) was simulated. Populations are assumed to be in drift–migration equilibrium with symmetric migration at a rate of m, which is the fraction of new migrants each generation. Sample size (n) is 50. (A) Sensitivity as a function of the degree of population subdivision, expressed as 4_Nm_ on the x_-axis. All genes were sampled from one subpopulation. (B) Sensitivity as a function of the sampling skewness; for example, 5/45 means 5 genes are sampled from one subpopulation and 45 from the other. In this case, 4_Nm = 0.1, a value at which the tests show sensitivity to population subdivision in A.

Similar articles

Cited by

References

    1. Braverman, J. M., R. R. Hudson, N. L. Kaplan, C. H. Langley and W. Stephan, 1995. The hitchhiking effect on the site frequency spectrum of DNA polymorphisms. Genetics 140: 783–796. - PMC - PubMed
    1. Bustamante, C. D., R. Nielsen, S. A. Sawyer, K. M. Olsen, M. D. Purugganan et al., 2002. The cost of inbreeding in Arabidopsis. Nature 416: 531–534. - PubMed
    1. Charlesworth, B., M. T. Morgan and D. Charlesworth, 1993. The effect of deleterious mutations on neutral molecular variation. Genetics 134: 1289–1303. - PMC - PubMed
    1. Charlesworth, D., B. Charlesworth and M. T. Morgan, 1995. The pattern of neutral molecular variation under the background selection model. Genetics 141: 1619–1632. - PMC - PubMed
    1. Fay, J. C., and C.-I Wu, 2000. Hitchhiking under positive Darwinian selection. Genetics 155: 1405–1413. - PMC - PubMed

Publication types

MeSH terms

Grants and funding

LinkOut - more resources