A genomewide single-nucleotide-polymorphism panel with high ancestry information for African American admixture mapping - PubMed (original) (raw)

A genomewide single-nucleotide-polymorphism panel with high ancestry information for African American admixture mapping

Chao Tian et al. Am J Hum Genet. 2006 Oct.

Abstract

Admixture mapping requires a genomewide panel of relatively evenly spaced markers that can distinguish the ancestral origins of chromosomal segments in admixed individuals. Through use of the results of the International HapMap Project and specific selection criteria, the current study has examined the ability of selected single-nucleotide polymorphisms (SNPs) to extract continental ancestry information in African American subjects and to explore parameters for admixture mapping. Genotyping of two linguistically diverse West African populations (Bini and Kanuri Nigerians, who are Niger-Congo [Bantu] and Nilo-Saharan speakers, respectively), European Americans, and African Americans validated a genomewide set of >4,000 SNP ancestry-informative markers with mean and median F(ST) values >0.59 and mean and median Fisher's information content >2.5. This set of SNPs extracted a larger amount of ancestry information in African Americans than previously reported SNP panels and provides nearly uniform coverage of the genome. Moreover, in the current study, simulations show that this more informative panel improves power for admixture mapping in African Americans when ethnicity risk ratios are modest. This is particularly important in the application of admixture mapping in complex genetic diseases for which only modest ethnicity risk ratios of relevant susceptibility genes are expected.

PubMed Disclaimer

Figures

Figure 1.

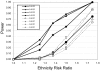
Figure 1.

δ of EURA/WAFR SNP AIMs. The SNP AIMs were arranged in ascending allele frequency in the AFA population, and, for each SNP, the WAFR SNP allele was chosen as the higher-frequency allele. Since AIM SNPs were chosen to maximize FIC, the majority of SNPs are close to fixation in the WAFR subjects. The data are based on nearly complete genotyping results in 84 EURA, 142 WAFR, and 96 AFA subjects.

Figure 2.

Figure 2.

Admixture-mapping distribution for each chromosome. The admixture-mapping information (ordinate) is shown for each position on the deCODE sex-averaged map. The information was determined using ADMIXMAP analysis of genotyping results of 4,222 SNPs typed in the AFA samples (96 subjects).

Figure 3.

Figure 3.

Power for admixture mapping as a function of admixture-mapping information. The power was determined from simulations with 700 cases, 700 controls, and SNP sets with admixture information corresponding to the legend for the SNP set used (see the “Analysis of Power Using Simulated Data Sets” and “Methods” sections). The power curves were determined using the ADMIXMAP program and deCODE genetic map for either case-only (CO) or case-control (CC) analyses. The appropriate α level for these analyses was a normalized score of 4.0, which was based on extensive simulations. The results are based on a minimum of 50 separate simulations and analysis for each measurement. Similar results were obtained using ANCESTRYMAP and MALDSOFT algorithms in more-limited analyses (data not shown).

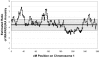
Figure 4.

Figure 4.

Estimated ratio of WAFR/EURA ancestry across chromosome 1 in 96 AFA individuals. The ancestry ratio was determined by scoring each marker on the basis of the assignment of ancestry (WAFR vs. EURA) in each predicted gamete (see the “Methods” section). For chromosome 1, a mean of 179 of a possible 192 chromosomes for each marker were scored as “WAFR” or “EURA” ancestry, with use of a log likelihood probability ratio >2. The figure shows the autosomal mean ±1 SD (gray rectangle).

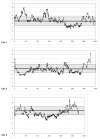
Figure 5.

Figure 5.

Estimated ratio of WAFR/EURA ancestry across each chromosome in 96 AFA individuals. The ratio was determined by scoring the ancestry of each marker on the basis of the assignment of ancestry (WAFR vs. EURA) in each predicted gamete (see the “Methods” section). For the autosomal chromosomes, a mean of 178 of a possible 192 chromosomes for each marker was scored as WAFR or EURA ancestry with use of a log likelihood probability ratio >2. For the autosomal chromosomes, the gray rectangle on each chromosome shows the autosomal mean ±1 SD (4.5±1.0). Similarly, for the X chromosome, the gray rectangle shows the mean ±1 SD (6.77±1.6). Many regions at the ends of chromosomes (qter and pter) show large deviations that correspond to decreased admixture information in these regions. The other deviations do not correlate with admixture information. As noted in the text, similar variations, although at different genomic positions, were found in simulations of 96 AFA individuals.

Figure 5.

Figure 5.

Estimated ratio of WAFR/EURA ancestry across each chromosome in 96 AFA individuals. The ratio was determined by scoring the ancestry of each marker on the basis of the assignment of ancestry (WAFR vs. EURA) in each predicted gamete (see the “Methods” section). For the autosomal chromosomes, a mean of 178 of a possible 192 chromosomes for each marker was scored as WAFR or EURA ancestry with use of a log likelihood probability ratio >2. For the autosomal chromosomes, the gray rectangle on each chromosome shows the autosomal mean ±1 SD (4.5±1.0). Similarly, for the X chromosome, the gray rectangle shows the mean ±1 SD (6.77±1.6). Many regions at the ends of chromosomes (qter and pter) show large deviations that correspond to decreased admixture information in these regions. The other deviations do not correlate with admixture information. As noted in the text, similar variations, although at different genomic positions, were found in simulations of 96 AFA individuals.

Figure 5.

Figure 5.

Estimated ratio of WAFR/EURA ancestry across each chromosome in 96 AFA individuals. The ratio was determined by scoring the ancestry of each marker on the basis of the assignment of ancestry (WAFR vs. EURA) in each predicted gamete (see the “Methods” section). For the autosomal chromosomes, a mean of 178 of a possible 192 chromosomes for each marker was scored as WAFR or EURA ancestry with use of a log likelihood probability ratio >2. For the autosomal chromosomes, the gray rectangle on each chromosome shows the autosomal mean ±1 SD (4.5±1.0). Similarly, for the X chromosome, the gray rectangle shows the mean ±1 SD (6.77±1.6). Many regions at the ends of chromosomes (qter and pter) show large deviations that correspond to decreased admixture information in these regions. The other deviations do not correlate with admixture information. As noted in the text, similar variations, although at different genomic positions, were found in simulations of 96 AFA individuals.

Figure 5.

Figure 5.

Estimated ratio of WAFR/EURA ancestry across each chromosome in 96 AFA individuals. The ratio was determined by scoring the ancestry of each marker on the basis of the assignment of ancestry (WAFR vs. EURA) in each predicted gamete (see the “Methods” section). For the autosomal chromosomes, a mean of 178 of a possible 192 chromosomes for each marker was scored as WAFR or EURA ancestry with use of a log likelihood probability ratio >2. For the autosomal chromosomes, the gray rectangle on each chromosome shows the autosomal mean ±1 SD (4.5±1.0). Similarly, for the X chromosome, the gray rectangle shows the mean ±1 SD (6.77±1.6). Many regions at the ends of chromosomes (qter and pter) show large deviations that correspond to decreased admixture information in these regions. The other deviations do not correlate with admixture information. As noted in the text, similar variations, although at different genomic positions, were found in simulations of 96 AFA individuals.

Figure 5.

Figure 5.

Estimated ratio of WAFR/EURA ancestry across each chromosome in 96 AFA individuals. The ratio was determined by scoring the ancestry of each marker on the basis of the assignment of ancestry (WAFR vs. EURA) in each predicted gamete (see the “Methods” section). For the autosomal chromosomes, a mean of 178 of a possible 192 chromosomes for each marker was scored as WAFR or EURA ancestry with use of a log likelihood probability ratio >2. For the autosomal chromosomes, the gray rectangle on each chromosome shows the autosomal mean ±1 SD (4.5±1.0). Similarly, for the X chromosome, the gray rectangle shows the mean ±1 SD (6.77±1.6). Many regions at the ends of chromosomes (qter and pter) show large deviations that correspond to decreased admixture information in these regions. The other deviations do not correlate with admixture information. As noted in the text, similar variations, although at different genomic positions, were found in simulations of 96 AFA individuals.

Figure 5.

Figure 5.

Estimated ratio of WAFR/EURA ancestry across each chromosome in 96 AFA individuals. The ratio was determined by scoring the ancestry of each marker on the basis of the assignment of ancestry (WAFR vs. EURA) in each predicted gamete (see the “Methods” section). For the autosomal chromosomes, a mean of 178 of a possible 192 chromosomes for each marker was scored as WAFR or EURA ancestry with use of a log likelihood probability ratio >2. For the autosomal chromosomes, the gray rectangle on each chromosome shows the autosomal mean ±1 SD (4.5±1.0). Similarly, for the X chromosome, the gray rectangle shows the mean ±1 SD (6.77±1.6). Many regions at the ends of chromosomes (qter and pter) show large deviations that correspond to decreased admixture information in these regions. The other deviations do not correlate with admixture information. As noted in the text, similar variations, although at different genomic positions, were found in simulations of 96 AFA individuals.

Figure 5.

Figure 5.

Estimated ratio of WAFR/EURA ancestry across each chromosome in 96 AFA individuals. The ratio was determined by scoring the ancestry of each marker on the basis of the assignment of ancestry (WAFR vs. EURA) in each predicted gamete (see the “Methods” section). For the autosomal chromosomes, a mean of 178 of a possible 192 chromosomes for each marker was scored as WAFR or EURA ancestry with use of a log likelihood probability ratio >2. For the autosomal chromosomes, the gray rectangle on each chromosome shows the autosomal mean ±1 SD (4.5±1.0). Similarly, for the X chromosome, the gray rectangle shows the mean ±1 SD (6.77±1.6). Many regions at the ends of chromosomes (qter and pter) show large deviations that correspond to decreased admixture information in these regions. The other deviations do not correlate with admixture information. As noted in the text, similar variations, although at different genomic positions, were found in simulations of 96 AFA individuals.

Figure 5.

Figure 5.

Estimated ratio of WAFR/EURA ancestry across each chromosome in 96 AFA individuals. The ratio was determined by scoring the ancestry of each marker on the basis of the assignment of ancestry (WAFR vs. EURA) in each predicted gamete (see the “Methods” section). For the autosomal chromosomes, a mean of 178 of a possible 192 chromosomes for each marker was scored as WAFR or EURA ancestry with use of a log likelihood probability ratio >2. For the autosomal chromosomes, the gray rectangle on each chromosome shows the autosomal mean ±1 SD (4.5±1.0). Similarly, for the X chromosome, the gray rectangle shows the mean ±1 SD (6.77±1.6). Many regions at the ends of chromosomes (qter and pter) show large deviations that correspond to decreased admixture information in these regions. The other deviations do not correlate with admixture information. As noted in the text, similar variations, although at different genomic positions, were found in simulations of 96 AFA individuals.

Similar articles

Cited by

References

Web Resources

    1. Institut für Humangenetik, http://ihg.gsf.de/cgi-bin/hw/hwa1.pl (for the FINETTI software)
    1. Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/ (for lupus, prostate cancer, diabetic nephropathy, multiple sclerosis, and osteoporosis)

References

    1. McKeigue PM (2005) Prospects for admixture mapping of complex traits. Am J Hum Genet 76:1–7 - PMC - PubMed
    1. Zhang C, Chen K, Seldin MF, Li H (2004) A hidden Markov modeling approach for admixture mapping based on case-control data. Genet Epidemiol 27:225–23910.1002/gepi.20021 - DOI - PubMed
    1. Zhu X, Cooper RS, Elston RC (2004) Linkage analysis of a complex disease through use of admixed populations. Am J Hum Genet 74:1136–1153 - PMC - PubMed
    1. Patterson N, Hattangadi N, Lane B, Lohmueller KE, Hafler DA, Oksenberg JR, Hauser SL, Smith MW, O’Brien SJ, Altshuler D, Daly MJ, Reich D (2004) Methods for high-density admixture mapping of disease genes. Am J Hum Genet 74:979–1000 - PMC - PubMed
    1. Montana G, Pritchard JK (2004) Statistical tests for admixture mapping with case-control and cases-only data. Am J Hum Genet 75:771–789 - PMC - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources