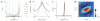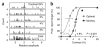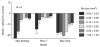Optimal decoding of correlated neural population responses in the primate visual cortex - PubMed (original) (raw)

. 2006 Nov;9(11):1412-20.

doi: 10.1038/nn1792. Epub 2006 Oct 22.

Affiliations

Optimal decoding of correlated neural population responses in the primate visual cortex

Yuzhi Chen et al. Nat Neurosci. 2006 Nov.

Abstract

Even the simplest environmental stimuli elicit responses in large populations of neurons in early sensory cortical areas. How these distributed responses are read out by subsequent processing stages to mediate behavior remains unknown. Here we used voltage-sensitive dye imaging to measure directly population responses in the primary visual cortex (V1) of monkeys performing a demanding visual detection task. We then evaluated the ability of different decoding rules to detect the target from the measured neural responses. We found that small visual targets elicit widespread responses in V1, and that response variability at distant sites is highly correlated. These correlations render most previously proposed decoding rules inefficient relative to one that uses spatially antagonistic center-surround summation. This optimal decoder consistently outperformed the monkey in the detection task, demonstrating the sensitivity of our techniques. Overall, our results suggest an unexpected role for inhibitory mechanisms in efficient decoding of neural population responses.

PubMed Disclaimer

Figures

Figure 1

Figure 1

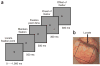
Behavioral task and recording chamber. (a) Task and stimulus (see Methods). (b) The cranial window over V1 in the left hemisphere in one monkey. The cortex is seen through a transparent artificial dura. A typical imaged area of 10 × 10 mm is indicated by the black square.

Figure 2

Figure 2

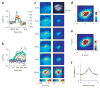
Neural population responses in V1 to a Gabor target (see Methods) measured with VSD imaging in one experiment. Gabor target parameters: σ = 0.33° , spatial frequency = 1.4 c.p.d., eccentricity = 2.7° . (a) Average time course of VSD responses. Response was measured in a small region of 0.25 × 0.25 mm, centered at the location of the small circle in c, bottom panels. Time courses are averaged across repetitions (n = 10 for each target contrast for target-present trials; n = 50 for target-absent trials). For display purposes, the average time course in target-absent trials is subtracted from each curve. Note that the animal was allowed to saccade to the target as soon as it was detected. Arrows indicate median reaction times at target contrasts in which at least three saccades were made. At high target contrasts, reaction times were short, leading to an early drop in the VSD response. (b) Single-trial time courses (thin lines) in the first 200 ms after target onset. The average time courses for each condition are shown in thick lines. (c) Spatial distribution of response amplitudes (left column) and response sensitivity (right column) for different target contrasts. Top right panel, image of cortical vasculature. To compute response amplitude, the response at each site is time averaged during a short interval after target onset and then averaged across repetitions (see Methods). Response sensitivity is measured as the signal-to-noise ratio d ′ (see text). Red squares in the bottom panels indicate the 8 × 8 mm ROI used for further data analysis. The circle indicates the site with maximal d ′ . Non uniform responses at 0% contrast (top left panel) represent residual noise in the mean response around large blood vessels. (d) Response amplitude in target-present trials averaged across all target contrasts after subtraction of the mean response in target-absent trials. (e) Two-dimensional Gaussian fit to the average response in d. (f) Average spatial correlations between pairs of sites as a function of their separation. To eliminate the effect of target contrast on spatial correlations, the average response (across repetitions) for each condition was first subtracted from the response in each trial before computing the correlations between the residual responses.

Figure 3

Figure 3

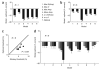
Optimal two-site and multiple-site pooling. (a) Each colored curve represents pooled sensitivity over two sites with different relative sensitivities as a function of the correlation between the sites (computed using equation (5), Supplementary Methods). Dashed vertical lines indicate the point of transition from positive pooling (on the left) to negative pooling (on the right). (b) Normalized falloff in sensitivity along the minor axis of the average response in Figure 2e (gray) and falloff in correlations along the same axis (black). (c) One-dimensional cut through the optimal whitening filter that, when convolved with the imaging responses, generates responses that are statistically independent across space. (d) Optimal set of weights obtained by convolving the whitening filter twice (see Methods) with the average response amplitude (Figure 2e). Note that the optimal filter contains a positive region at the center and a large negative region in the surround.

Figure 4

Figure 4

Methods for measuring neural and behavioral detection sensitivity. (a) Distributions of the VSD responses in the example experiment, pooled over an area of ~8 × 8 mm of cortex using the optimal set of weights (Fig. 3d). Pooled responses in target-present trials (gray) and target-absent trials (black) are separated according to target contrast. The bottom panel shows combined distributions across all target-present and all target-absent trials. The vertical line represents an optimally placed criterion for separating target-present trials from target-absent trials (see text). (b) Proportion of trials in which the observer reported that the target was present as a function of target contrast. Zero contrast represents target-absent trials (the probability at this point is the false alarm rate). Black triangles, monkey’s performance. Gray circles, performance of an observer that uses the Optimal rule to pool V1 responses. Solid curves are the best fitting Weibull functions. The dashed vertical lines and the corresponding numbers are the thresholds (see Methods). The model’s detection threshold was significantly lower than the monkey’s detection threshold (bootstrap test, P < 0.001). Horizontal error bars indicate 95% confidence interval. The model’s threshold was still significantly lower than the monkey’s threshold even with suboptimal criterion that reduced the false alarm rate of the model to a level comparable to that of the monkey.

Figure 5

Figure 5

Comparing detection sensitivity of candidate pooling rules. (a) Difference in overall percent correct between the first six pooling rules from Table 1 and the Optimal rule, in the example experiment. Asterisks indicate rules with performance significantly different from the Optimal (bootstrap test, P < 0.05; error bars = 95% confidence interval). (b) Average difference across all eight experiments in overall percent correct between the six pooling rules and the Optimal rule. Same conventions as in a. Asterisks indicate rules with performance significantly different from the Optimal rule across experiments (paired t-test, n = 8). (c) Scatter plot of threshold for the Optimal pooling rule vs. the monkeys. Filled symbols indicate experiments in which the Optimal model’s detection threshold was significantly lower than the monkey’s threshold (bootstrap test, P < 0.05). Error bars indicate one s.e.m. centered on the mean. (d) Average difference in overall percent correct between the Optimal rule using an 8 × 8 mm pooling area and the seven pooling rules at three pooling areas (2 × 2 mm, light gray; 4 × 4 mm, dark gray; 8 × 8 mm, black). Error bars in b and d show one s.e.m.

Figure 6

Figure 6

Effect of spatial binning on accuracy of the three pooling rules that rely on the response in a single site. Each bar indicates the difference in percent correct between the three pooling models at different bin size and the Optimal rule at the original bin size. Pooling rules that combine signals from a large area were relatively insensitive to the site size. For example, the Mean Amplitude rule gives exactly the same results irrespective of the site size. Error bars = one s.e.m.

Figure 7

Figure 7

Effects of timing parameters on the accuracy of the seven pooling rules. (a) A diagram illustrating the four timing parameters used in our analysis. VSD signals at each site in each trial were first normalized by the average signal during a short normalization interval (blue bar) and then averaged during a short temporal interval (light red bar). The averaging interval started at a fixed time after stimulus onset (Start) and ended either at a fixed time before saccade initiation (the beginning of a Motor prep., green bar), or, if saccade did not occur or was sufficiently late, at the maximal time of averaging (Max end avg.). In the example in the diagram, the averaging period ends before the maximal averaging time because the maximal averaging interval and the motor preparation interval overlap (dark red region). (b–e) The average difference in percent correct between the Optimal rule using the default timing parameters and each of the seven models using different combinations of timing parameters, averaged over the eight experiments. (b) Effect of start time. (c) Effect of maximal averaging time. (d) Effect of normalization period duration. (e) Effect of motor preparation duration. Dashed blue vertical lines indicate default values.

Similar articles

Cited by

References

    1. Woolsey CN. The Biology of Mental Health and Disease. Hoeber; New York: 1952. pp. 193–206.
    1. Hubel DH, Weisel TN. Ferrier lecture. Functional architecture of macaque monkey visual cortex. Proc R Soc Lond B. 1977;198:1–59. - PubMed
    1. Knudsen EI, Lac S, Esterly SD. Computational maps in the brain. Annu Rev Neurosci. 1987;10:41–65. - PubMed
    1. de Valois RL, de Valois KK. Spatial Vision. Oxford Univ. Press; New York: 1988.
    1. Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J Neurosci. 1982;2:1527–1537. - PMC - PubMed

Publication types

MeSH terms

LinkOut - more resources