Systematic pathway analysis using high-resolution fitness profiling of combinatorial gene deletions - PubMed (original) (raw)

. 2007 Feb;39(2):199-206.

doi: 10.1038/ng1948. Epub 2007 Jan 7.

Affiliations

Systematic pathway analysis using high-resolution fitness profiling of combinatorial gene deletions

Robert P St Onge et al. Nat Genet. 2007 Feb.

Abstract

Systematic genetic interaction studies have illuminated many cellular processes. Here we quantitatively examine genetic interactions among 26 Saccharomyces cerevisiae genes conferring resistance to the DNA-damaging agent methyl methanesulfonate (MMS), as determined by chemogenomic fitness profiling of pooled deletion strains. We constructed 650 double-deletion strains, corresponding to all pairings of these 26 deletions. The fitness of single- and double-deletion strains were measured in the presence and absence of MMS. Genetic interactions were defined by combining principles from both statistical and classical genetics. The resulting network predicts that the Mph1 helicase has a role in resolving homologous recombination-derived DNA intermediates that is similar to (but distinct from) that of the Sgs1 helicase. Our results emphasize the utility of small molecules and multifactorial deletion mutants in uncovering functional relationships and pathway order.

PubMed Disclaimer

Figures

Figure 1

Figure 1

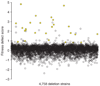
Identification of genes that confer resistance to MMS. Chemogenomic profiling of the homozygous diploid (BY4743) collection of deletion mutants with MMS. Fitness defect scores, based on barcode microarray hybridization and calculated as described, are plotted on the y axis for 4,758 deletion strains arranged alphabetically across the x axis. Twenty-six deletion strains that were analyzed further are highlighted in yellow. MMS-sensitive strains showing severe growth defects in the absence of MMS, or corresponding to deletions that overlapped other genes in the selected set, were not pursued further.

Figure 2

Figure 2

Fitness measurement of single- and double-deletion strains. (a) Calculation of the doubling time (D) of individual deletion strains during exponential growth. D is the difference between the time tf at an arbitrary maximum OD (ODm) and the time ti at a point three generations earlier (ODm−3), divided by the number of generations (D =(tf – ti)/3). (b) Mean fitness of 26 single-deletion strains in 0.002% MMS. Fitness (W) for a strain with gene x deleted was calculated by dividing the average D of wild type (Y5563) by that of the deletion strain (W =Dwt /_Dyfg_Δ). Fitness values were averaged from MATa Kanr (BY4741) and MATα Natr (BY4742) deletion strains; error bars represent the s.d. from no fewer than seven replicate measurements. (c) Fitness correlation between reciprocal double-deletion mutants for each unique gene pair in the presence and absence of MMS. The fitness of Kanr-Natr double-deletion strains is plotted on the y axis and the Natr-Kanr fitness is plotted on the x axis. The correlation coefficient (R) and best-fitting line are shown.

Figure 3

Figure 3

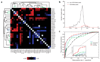
Quantitative genetic interactions predict shared function. (a) Genes clustered according to similar patterns of deviation (ε) of double-deletion fitness (Wxy) from the expectation for non-interacting loci (Wx × Wy). Fitness values were obtained from growth in the presence of 0.002% MMS. Hierarchical clustering of genes was performed on the basis of genetic congruence (Pearson correlation of ε profiles). (b) Distribution of ε values for all gene pairs grown in the presence of MMS (bin size 0.025). Gene pairs with specific functional links are in red (GO-linked pairs); gene pairs not sharing specific functional links are in black (non-GO–linked pairs). (c) Comparison of the ability to predict functional links of ε values, genetic congruence of ε profiles, and _Z_-scores assessing the proximity of the MMS sensitivity of double-deletion strains to the sensitivity of single-deletion strains. The combination of each of these is also assessed (‘Combined’ ). For each predictor, the true-positive rate or ‘sensitivity’ (defined here as the fraction of gene pairs correctly predicted to have functional links) and false-positive rate or ‘1 − specificity’ (defined here as the fraction of non-functionally linked gene pairs incorrectly predicted to have functional links) are shown at a series of score thresholds.

Figure 4

Figure 4

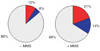
Identification of significant genetic interactions. Significant departure (P < 0.01) from a multiplicative model in which Wxy = Wx × Wy is used to define aggravating and alleviating genetic interactions. The percentage of aggravating (red), alleviating (blue) and neutral (gray) gene pairs identified are compared in the presence and absence of MMS.

Figure 5

Figure 5

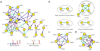
Subclassification of alleviating interactions. (a) Subclassification of 45 alleviating interactions on the basis of similarity of MMS sensitivity (S = D+MMS/_D_−MMS) of each double-deletion strain (Sxy) to its corresponding single-deletion strains (Sx and Sy), as measured by _Z_-scores (see Methods). Genes are represented by nodes. Arrows represent five alleviating interaction subtypes: coequal (green), partial masking (light blue), masking (dark blue), partial suppression (purple), suppression (pink). These interaction types are shown below (red arrowheads indicate single-deletion MMS sensitivities; colored circles represent double-deletion sensitivities). (b) Ten coequal interactions identify functionally cohesive units. Nine correspond to known or predicted protein interactions, as indicated by the broken circles. (c) Asymmetric alleviating interactions (Sx > Sy) between core members of the homologous recombination pathway (RAD51, RAD52, RAD54, RAD55 and RAD57). For masking interactions (both partial and complete), arrows are drawn from the masking locus (x); for suppressing interactions (both partial and complete), arrows are drawn from the suppressing locus (y). (d) Partial suppression of the MMS sensitivities of _sgs1_Δ and _rad54_Δ by deletions in Shu complex genes (SHU1, SHU2, CSM2 and PSY3).

Figure 6

Figure 6

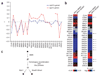
Predicted role of Mph1 in resolving homologous recombination–generated DNA intermediates. (a) Line graph emphasizing the similarity in ε profiles of _sgs1_Δ (red) and _mph1_Δ (blue). Deviation from multiplicative expectation (ε) is plotted on the y axis and genes are arranged alphabetically on the x axis. (b) Heat map representing the effect of 26 gene deletions (vertical axis) on the fitness of _mph1_Δ_mms4_Δ and _mph1_Δ_mus81_Δ double-deletion strains (horizontal axis). Raw ε values (where ε = Wxyz − Wxy × Wz) are shown on the left; significant deviations (P < 0.01) from expectation are represented on the right. Ten genes found to be consistently alleviating (arrows) were analyzed further (Supplementary Fig. 5). (c) Model of the potential role of MPH1 in resolving homologous recombination-dependent DNA intermediates (●, undamaged DNA; ∅, MMS-damaged DNA;⊗, toxic DNA intermediates).

Comment in

Similar articles

Cited by

References

    1. Phillips PC. The language of gene interaction. Genetics. 1998;149:1167–1171. - PMC - PubMed
    1. Phillips PC, Otto SP, Whitlock MC. Beyond the Average: the Evolutionary Importance of Gene Interactions and Variability of Epistatic Effects in Epistasis and the Evolutionary Process. New York: Oxford Univ. Press; 2000. pp. 20–38.
    1. Kondrashov AS. Deleterious mutations and the evolution of sexual reproduction. Nature. 1998;336:435–440. - PubMed
    1. Szafraniec K, Wloch DM, Sliwa P, Borts RH, Korona R. Small fitness effects and weak genetic interactions between deleterious mutations in heterozygous loci of the yeast Saccharomyces cerevisiae. Genet. Res. 2003;82:19–31. - PubMed
    1. Elena SF, Lenski RE. Test of synergistic interactions among deleterious mutations in bacteria. Nature. 1997;390:395–398. - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources