Forward-time simulations of human populations with complex diseases - PubMed (original) (raw)
Forward-time simulations of human populations with complex diseases
Bo Peng et al. PLoS Genet. 2007.
Abstract
Due to the increasing power of personal computers, as well as the availability of flexible forward-time simulation programs like simuPOP, it is now possible to simulate the evolution of complex human diseases using a forward-time approach. This approach is potentially more powerful than the coalescent approach since it allows simulations of more than one disease susceptibility locus using almost arbitrary genetic and demographic models. However, the application of such simulations has been deterred by the lack of a suitable simulation framework. For example, it is not clear when and how to introduce disease mutants-especially those under purifying selection-to an evolving population, and how to control the disease allele frequencies at the last generation. In this paper, we introduce a forward-time simulation framework that allows us to generate large multi-generation populations with complex diseases caused by unlinked disease susceptibility loci, according to specified demographic and evolutionary properties. Unrelated individuals, small or large pedigrees can be drawn from the resulting population and provide samples for a wide range of study designs and ascertainment methods. We demonstrate our simulation framework using three examples that map genes associated with affection status, a quantitative trait, and the age of onset of a hypothetical cancer, respectively. Nonadditive fitness models, population structure, and gene-gene interactions are simulated. Case-control, sibpair, and large pedigree samples are drawn from the simulated populations and are examined by a variety of gene-mapping methods.
Conflict of interest statement
Competing interests. The authors have declared that no competing interests exist.
Figures
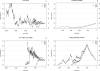
Figure 1. Examples of Simulated Trajectories
Trajectories of simulated allele frequency under different selection models. For each selection model, 100 replicates are simulated and three trajectories corresponding to the 5%, 50%, and 95% quantiles of the trajectory length are plotted. The selection models are neutral (left top, s 1 = s 2 = 0), advantageous (right top, s 1 = 0.001 and s 2 = 0.002), deleterious (left bottom, s 1 = −0.001 and s 2 = −0.002) and a mixed-selection model (right bottom) in which the disease allele is advantageous before 2,000 generations ago (s 1 = 0.001 and s 2 = 0.002) and is under purifying selection in the recent 2,000 generations (s 1 = −0.001 and s 2 = −0.002). In all cases, the current allele frequency is 10%. The population size is
such that N(10,000) = 106. Note that one of the trajectories in the left bottom panel is longer than 20,000 generations and its allele frequency is more than 0.5 before generation 10,000.
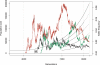
Figure 2. Illustration of the Evolutionary Scenario
Illustration of the evolutionary scenario of a simulation with three DSL. Demographic model (left axis): The population starts at size 10,000 and begins to grow exponentially at generation 4,000. The population is split into five equal-sized subpopulations at generation 7,500 (with subpopulations separated with solid lines) and reaches size 2 × 105 at generation 10,000. Migration is allowed from generation 9,500 to 10,000 (with subpopulations separated by dashed lines). Disease allele frequencies (right axis): The DSL are under advantageous selection pressure, with fitnesses of 1, 1.0001, and 1.0002 for genotypes AA, Aa, and aa, respectively, where a is the disease susceptibility allele. The present disease allele frequencies are 0.01, 0.02, and 0.03, respectively. The trajectories simulated backward in time are plotted in solid lines with different colors. The trajectories obtained during forward-time controlled random mating are plotted as dotted lines, which are indistinguishable from the simulated trajectories.
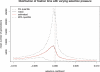
Figure 3. Validation of Trajectory Lengths
Mean, 5%, and 95% quantile of the length of trajectories of a mutant under different selection pressure. The mutant starts at allele frequency 0.1, evolves backward in time in a constant population with size N = 5,000, and is subjected to constant selection pressure with a selection coefficient s of −0.001 to 0.001, until it is lost or fixed. The red smooth curve represents theoretical estimates of the mean number of generations before this mutant is lost or fixed. Note that the simulated trajectories that are fixed or have more than one mutant at generation 1 are also accepted, in accordance with the theoretical estimates.
Similar articles
- GENOMEPOP: a program to simulate genomes in populations.
Carvajal-Rodríguez A. Carvajal-Rodríguez A. BMC Bioinformatics. 2008 Apr 30;9:223. doi: 10.1186/1471-2105-9-223. BMC Bioinformatics. 2008. PMID: 18447924 Free PMC article. - SUP: an extension to SLINK to allow a larger number of marker loci to be simulated in pedigrees conditional on trait values.
Lemire M. Lemire M. BMC Genet. 2006 Jul 3;7:40. doi: 10.1186/1471-2156-7-40. BMC Genet. 2006. PMID: 16803631 Free PMC article. - simuPOP: a forward-time population genetics simulation environment.
Peng B, Kimmel M. Peng B, et al. Bioinformatics. 2005 Sep 15;21(18):3686-7. doi: 10.1093/bioinformatics/bti584. Epub 2005 Jul 14. Bioinformatics. 2005. PMID: 16020469 - On selecting markers for association studies: patterns of linkage disequilibrium between two and three diallelic loci.
Garner C, Slatkin M. Garner C, et al. Genet Epidemiol. 2003 Jan;24(1):57-67. doi: 10.1002/gepi.10217. Genet Epidemiol. 2003. PMID: 12508256 Review. - Mapping genes through the use of linkage disequilibrium generated by genetic drift: 'drift mapping' in small populations with no demographic expansion.
Terwilliger JD, Zöllner S, Laan M, Pääbo S. Terwilliger JD, et al. Hum Hered. 1998 May-Jun;48(3):138-54. doi: 10.1159/000022794. Hum Hered. 1998. PMID: 9618061 Review.
Cited by
- Selecting among Alternative Scenarios of Human Evolution by Simulated Genetic Gradients.
Branco C, Arenas M. Branco C, et al. Genes (Basel). 2018 Oct 18;9(10):506. doi: 10.3390/genes9100506. Genes (Basel). 2018. PMID: 30340387 Free PMC article. Review. - Simulating variance heterogeneity in quantitative genome wide association studies.
Al Kawam A, Alshawaqfeh M, Cai JJ, Serpedin E, Datta A. Al Kawam A, et al. BMC Bioinformatics. 2018 Mar 21;19(Suppl 3):72. doi: 10.1186/s12859-018-2061-1. BMC Bioinformatics. 2018. PMID: 29589560 Free PMC article. - A Bayesian approach to identify genes and gene-level SNP aggregates in a genetic analysis of cancer data.
Stingo FC, Swartz MD, Vannucci M. Stingo FC, et al. Stat Interface. 2015;8(2):137-151. doi: 10.4310/SII.2015.v8.n2.a2. Stat Interface. 2015. PMID: 28989562 Free PMC article. - A pivot mutation impedes reverse evolution across an adaptive landscape for drug resistance in Plasmodium vivax.
Ogbunugafor CB, Hartl D. Ogbunugafor CB, et al. Malar J. 2016 Jan 25;15:40. doi: 10.1186/s12936-016-1090-3. Malar J. 2016. PMID: 26809718 Free PMC article. - ARG-walker: inference of individual specific strengths of meiotic recombination hotspots by population genomics analysis.
Chen H, Yang P, Guo J, Kwoh CK, Przytycka TM, Zheng J. Chen H, et al. BMC Genomics. 2015;16 Suppl 12(Suppl 12):S1. doi: 10.1186/1471-2164-16-S12-S1. Epub 2015 Dec 9. BMC Genomics. 2015. PMID: 26679564 Free PMC article.
References
- Kruglyak L. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat Genet. 1999;22:139–44. - PubMed
- Balloux F, Goudet J. Statistical properties of population differentiation estimators under stepwise mutation in a finite island model. Mol Ecol. 2002;11:771–783. - PubMed
- Kingman J. The coalescent. Stochastic Processes Appl. 1982;13:235–248.
- Griffiths RC. Neutral two-locus multiple allele models with recombination. Theor Popul Biol. 1981;19:169–186.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources