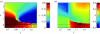Participation costs dismiss the advantage of heterogeneous networks in evolution of cooperation - PubMed (original) (raw)
Participation costs dismiss the advantage of heterogeneous networks in evolution of cooperation
Naoki Masuda. Proc Biol Sci. 2007.
Abstract
Real social interactions occur on networks in which each individual is connected to some, but not all, of others. In social dilemma games with a fixed population size, heterogeneity in the number of contacts per player is known to promote evolution of cooperation. Under a common assumption of positively biased pay-off structure, well-connected players earn much by playing frequently, and cooperation once adopted by well-connected players is unbeatable and spreads to others. However, maintaining a social contact can be costly, which would prevent local pay-offs from being positively biased. In replicator-type evolutionary dynamics, it is shown that even a relatively small participation cost extinguishes the merit of heterogeneous networks in terms of cooperation. In this situation, more connected players earn less so that they are no longer spreaders of cooperation. Instead, those with fewer contacts win and guide the evolution. The participation cost, or the baseline pay-off, is irrelevant in homogeneous populations, but is essential for evolutionary games on heterogeneous networks.
Figures
Figure 1
The Prisoner's Dilemma on the scale-free networks with participation costs. The pay-off matrix is represented by equation (3.2). (a) The final fraction of cooperators _c_f**.** (b) c_f for the scale-free networks shown in (a) −_c_f for the regular random graph shown in the electronic supplementary material figure 1_a.
Figure 2
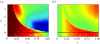
The effect of the number of neighbours in the Prisoner's Dilemma on the scale-free networks. (a) The average generation pay-off and (b) the average number of flips are plotted in terms of the number of neighbours that a player has. Note that the log scale is used for the abscissa of (b) for clarity. The lines correspond to _h_=0 (thinnest line), 0.2, 0.23, 0.24, 0.25, 0.3 and 0.5 (thickest line). The pay-off matrix is given by equation (3.2) with _T_=1.5.
Figure 3
The snowdrift game on the scale-free networks with participation costs. (a) _c_f and (b) _c_f for the scale-free networks shown in (a) −_c_f for the regular random graph shown in the electronic supplementary material figure 2.
Figure 4
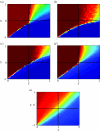
_c_f in the T_–_S space for (a) the regular random graph and the scale-free networks with (b) _h_=0, (c) _h_=0.5, (d) _h_=1 and (e) _h_=2.
Similar articles
- The effect of sanctions on the evolution of cooperation in linear division of labor.
Nakamaru M, Shimura H, Kitakaji Y, Ohnuma S. Nakamaru M, et al. J Theor Biol. 2018 Jan 21;437:79-91. doi: 10.1016/j.jtbi.2017.10.007. Epub 2017 Oct 17. J Theor Biol. 2018. PMID: 29054813 - Evolutionary games and population dynamics: maintenance of cooperation in public goods games.
Hauert C, Holmes M, Doebeli M. Hauert C, et al. Proc Biol Sci. 2006 Oct 7;273(1600):2565-70. doi: 10.1098/rspb.2006.3600. Proc Biol Sci. 2006. PMID: 16959650 Free PMC article. - Evolutionary dynamics of social dilemmas in structured heterogeneous populations.
Santos FC, Pacheco JM, Lenaerts T. Santos FC, et al. Proc Natl Acad Sci U S A. 2006 Feb 28;103(9):3490-4. doi: 10.1073/pnas.0508201103. Epub 2006 Feb 16. Proc Natl Acad Sci U S A. 2006. PMID: 16484371 Free PMC article. - Coevolutionary games--a mini review.
Perc M, Szolnoki A. Perc M, et al. Biosystems. 2010 Feb;99(2):109-25. doi: 10.1016/j.biosystems.2009.10.003. Epub 2009 Oct 29. Biosystems. 2010. PMID: 19837129 Review. - Universal scaling for the dilemma strength in evolutionary games.
Wang Z, Kokubo S, Jusup M, Tanimoto J. Wang Z, et al. Phys Life Rev. 2015 Sep;14:1-30. doi: 10.1016/j.plrev.2015.04.033. Epub 2015 May 5. Phys Life Rev. 2015. PMID: 25979121 Review.
Cited by
- Learning and innovative elements of strategy adoption rules expand cooperative network topologies.
Wang S, Szalay MS, Zhang C, Csermely P. Wang S, et al. PLoS One. 2008 Apr 9;3(4):e1917. doi: 10.1371/journal.pone.0001917. PLoS One. 2008. PMID: 18398453 Free PMC article. - Bipartite graphs as models of population structures in evolutionary multiplayer games.
Peña J, Rochat Y. Peña J, et al. PLoS One. 2012;7(9):e44514. doi: 10.1371/journal.pone.0044514. Epub 2012 Sep 10. PLoS One. 2012. PMID: 22970237 Free PMC article. - Emergence of scale-free characteristics in socio-ecological systems with bounded rationality.
Kasthurirathna D, Piraveenan M. Kasthurirathna D, et al. Sci Rep. 2015 Jun 11;5:10448. doi: 10.1038/srep10448. Sci Rep. 2015. PMID: 26065713 Free PMC article. - Inequality as information: Wealth homophily facilitates the evolution of cooperation.
Johnson T, Smirnov O. Johnson T, et al. Sci Rep. 2018 Aug 2;8(1):11605. doi: 10.1038/s41598-018-30052-1. Sci Rep. 2018. PMID: 30072773 Free PMC article. - Evolutionary Constraints on Connectivity Patterns in the Mammalian Suprachiasmatic Nucleus.
Spencer C, Tripp E, Fu F, Pauls S. Spencer C, et al. Front Netw Physiol. 2021 Aug 19;1:716883. doi: 10.3389/fnetp.2021.716883. eCollection 2021. Front Netw Physiol. 2021. PMID: 36925572 Free PMC article.
References
- Abramson G, Kuperman M. Social games in a social network. Phys. Rev. E. 2001;63:030901(R). doi:10.1103/PhysRevE.63.030901 - DOI - PubMed
- Axelrod R. Basic Books; New York, NY: 1984. Evolution of cooperation.
- Bala V, Goyal S. A noncooperative model of network formation. Econometrica. 2000;68:1181–1229. doi:10.1111/1468-0262.00155 - DOI
- Barabási A.-L, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi:10.1126/science.286.5439.509 - DOI - PubMed
- Dawes R.M. Social dilemmas. Annu. Rev. Psychol. 1980;31:169–193. doi:10.1146/annurev.ps.31.020180.001125 - DOI
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous