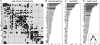Network structure of cerebral cortex shapes functional connectivity on multiple time scales - PubMed (original) (raw)
Network structure of cerebral cortex shapes functional connectivity on multiple time scales
Christopher J Honey et al. Proc Natl Acad Sci U S A. 2007.
Abstract
Neuronal dynamics unfolding within the cerebral cortex exhibit complex spatial and temporal patterns even in the absence of external input. Here we use a computational approach in an attempt to relate these features of spontaneous cortical dynamics to the underlying anatomical connectivity. Simulating nonlinear neuronal dynamics on a network that captures the large-scale interregional connections of macaque neocortex, and applying information theoretic measures to identify functional networks, we find structure-function relations at multiple temporal scales. Functional networks recovered from long windows of neural activity (minutes) largely overlap with the underlying structural network. As a result, hubs in these long-run functional networks correspond to structural hubs. In contrast, significant fluctuations in functional topology are observed across the sequence of networks recovered from consecutive shorter (seconds) time windows. The functional centrality of individual nodes varies across time as interregional couplings shift. Furthermore, the transient couplings between brain regions are coordinated in a manner that reveals the existence of two anticorrelated clusters. These clusters are linked by prefrontal and parietal regions that are hub nodes in the underlying structural network. At an even faster time scale (hundreds of milliseconds) we detect individual episodes of interregional phase-locking and find that slow variations in the statistics of these transient episodes, contingent on the underlying anatomical structure, produce the transfer entropy functional connectivity and simulated blood oxygenation level-dependent correlation patterns observed on slower time scales.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
Fig. 1.
Structural connectivity and network hubs. (A) Large-scale anatomical connection matrix of macaque neocortex. (B) Ranking of areas for flow/clustering ratio. Flow/clustering ratios for each region are compared with those obtained from 1,000 degree-matched, randomized networks. Regions with significantly increased flow/clustering ratio (P < 0.05, uncorrected) are shown in dark gray. (_C_) Ranking of areas for betweenness centrality. Regions with significantly increased (_P_ < 0.05) centrality are shown in dark gray. (_D_) Ranking of areas for motif count of the motif class shown in _Inset_. Dark gray bars indicate that the area shows increased motif counts (_z_-score > 2) relative to random and lattice controls.
Fig. 2.
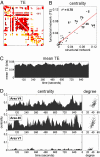
Topology of functional networks and hub dynamics. (A) Example of a functional TE network, calculated using a 240,000 time step data segment (240 sec). The functional matrix has been thresholded to yield a binary network with connection density equal to that of the structural network (505 connections). Comparison between structural and functional networks allows the distinction of true positives (TP functional connections that match existing structural connections; shown in red), as well as false positives (FP functional connections absent in the structural matrix; shown in dark red) and false negatives (FN structural connections absent in the functional network; shown in yellow). Numerals give the count of TP and FP (TP + FP = 505; FP = FN at this threshold). (B) Correlation between centrality of each node within structural and TE functional network (mean of n = 5, obtained from 240-sec data segments): _r_2 = 0.78. (C) Time course of TE averaged over the entire network: 960,000 time steps (16 min) windowed into 156 overlapping data segments, 30,000 time steps each, consecutively offset by 6,000 time steps (6 sec). (D) Corresponding time course for betweenness centrality for two putative hub regions (area V4, Top, and area 46, Middle) and one non-hub region (area V1, Bottom). Scatter plots at right show the relationship between degree and centrality for these nodes across the 156 functional networks.
Fig. 3.
Anticorrelated functional clusters. (A) Degree correlation matrix capturing cross-regional correlations in gains and losses of thresholded functional connections. Matrix represents an average over four 960,000 time step (960-sec) runs, sampled as in Fig. 2 C and D. Cluster analysis yields two main clusters (blue, occipitotemporal; green, parietofrontal). (B) Anatomical location of main clusters in Caret coordinates (51). Areas intermediate in terms of degree correlations are shaded in light blue (areas STPa, STPp, TH, TF, 7a, and 46). (C) Difference in the mean within-cluster TE over time (for the same run shown in Fig. 2 C and D), expressed as percentage of mean signal. (D) TE difference profiles for four runs using intact (Fig. 1_A_) corticocortical connections (Upper), and four runs carried out in randomized networks preserving in- and out-degree of each node (Lower). Cluster analysis was performed on degree correlation matrices for each separate run to obtain two main clusters. Clusters were then used to calculate differences in mean TE. Standard deviations, expressed as percent baseline TE, are significantly different (two-tailed t test, P < 0.005) for the two groups.
Fig. 4.
Estimated BOLD signals and relation to synchrony. (A) BOLD correlation matrix, computed from estimated BOLD time series after regressing out global BOLD fluctuations and sampled every 2 sec. Matrix represents an average over four 960,000 time step runs (960 sec, as in Fig. 3). (B) Correlation map obtained by using areas V4 and SII as seed regions, labeling all positively correlated brain regions in either blue (V4) or green (SII). V4 and SII were chosen because they occupy central positions within their respective clusters. Regions not showing positive correlations, or positively correlated with both seed regions, are shown in light blue. (C) Scatter plot of global BOLD signal against variations in aggregate network TE, for corresponding 30-sec data segments obtained from four runs of 960 sec. (D) Scatter plot of global BOLD signal against variations in synchronization. Synchronization is measured as the percentage of phase-locked time steps (in-phase or anti-phase) across all node pairs. (E) BOLD signal and synchrony shown over a 95-sec data segment recorded from area 7a. Synchrony is calculated as the total time that area 7a is phase-locked with any of the other nodes in the network.
Similar articles
- Theoretical neuroanatomy and the connectivity of the cerebral cortex.
Sporns O, Tononi G, Edelman GM. Sporns O, et al. Behav Brain Res. 2002 Sep 20;135(1-2):69-74. doi: 10.1016/s0166-4328(02)00157-2. Behav Brain Res. 2002. PMID: 12356436 - Do the Different Sensory Areas Within the Cat Anterior Ectosylvian Sulcal Cortex Collectively Represent a Network Multisensory Hub?
Meredith MA, Wallace MT, Clemo HR. Meredith MA, et al. Multisens Res. 2018 Jan;31(8):793-823. doi: 10.1163/22134808-20181316. Epub 2018 Jun 26. Multisens Res. 2018. PMID: 31157160 Free PMC article. Review. - Rich club organization of macaque cerebral cortex and its role in network communication.
Harriger L, van den Heuvel MP, Sporns O. Harriger L, et al. PLoS One. 2012;7(9):e46497. doi: 10.1371/journal.pone.0046497. Epub 2012 Sep 28. PLoS One. 2012. PMID: 23029538 Free PMC article. - The relation between structural and functional connectivity patterns in complex brain networks.
Stam CJ, van Straaten EC, Van Dellen E, Tewarie P, Gong G, Hillebrand A, Meier J, Van Mieghem P. Stam CJ, et al. Int J Psychophysiol. 2016 May;103:149-60. doi: 10.1016/j.ijpsycho.2015.02.011. Epub 2015 Feb 10. Int J Psychophysiol. 2016. PMID: 25678023 - Cortical cores in network dynamics.
de Pasquale F, Corbetta M, Betti V, Della Penna S. de Pasquale F, et al. Neuroimage. 2018 Oct 15;180(Pt B):370-382. doi: 10.1016/j.neuroimage.2017.09.063. Epub 2017 Sep 30. Neuroimage. 2018. PMID: 28974453 Review.
Cited by
- Influence of individual's age on the characteristics of brain effective connectivity.
Nourzadegan N, Baghernezhad S, Daliri MR. Nourzadegan N, et al. Geroscience. 2024 Nov 16. doi: 10.1007/s11357-024-01436-1. Online ahead of print. Geroscience. 2024. PMID: 39549197 - A within-subject voxel-wise constant-block partial least squares correlation method to explore MRI-based brain structure-function relationship.
Zhao X, Chen K, Wang H, Gao Y, Ji X, Li Y. Zhao X, et al. Cogn Neurodyn. 2024 Jun;18(3):813-827. doi: 10.1007/s11571-023-09941-3. Epub 2023 Feb 18. Cogn Neurodyn. 2024. PMID: 39539980 - The brain's first "traffic map" through Unified Structural and Functional Connectivity (USFC) modeling.
Has Silemek AC, Chen H, Sati P, Gao W. Has Silemek AC, et al. Commun Biol. 2024 Nov 9;7(1):1477. doi: 10.1038/s42003-024-07160-y. Commun Biol. 2024. PMID: 39521849 Free PMC article. - Competitive interactions shape brain dynamics and computation across species.
Luppi AI, Sanz Perl Y, Vohryzek J, Mediano PAM, Rosas FE, Milisav F, Suarez LE, Gini S, Gutierrez-Barragan D, Gozzi A, Misic B, Deco G, Kringelbach ML. Luppi AI, et al. bioRxiv [Preprint]. 2024 Oct 22:2024.10.19.619194. doi: 10.1101/2024.10.19.619194. bioRxiv. 2024. PMID: 39484469 Free PMC article. Preprint. - Sex Differences in Hierarchical and Modular Organization of Functional Brain Networks: Insights from Hierarchical Entropy and Modularity Analysis.
Chen W, Zhan L, Jia T. Chen W, et al. Entropy (Basel). 2024 Oct 14;26(10):864. doi: 10.3390/e26100864. Entropy (Basel). 2024. PMID: 39451941 Free PMC article.
References
- Bressler SL. Brain Res Rev. 1995;20:288–304. - PubMed
- Gray CM, Singer W. Annu Rev Neurosci. 1995;18:555–586. - PubMed
- Varela F, Lachaux J-P, Rodriguez E, Martinerie J. Nat Rev Neurosci. 2001;2:229–239. - PubMed
- Buszáki G, Draguhn A. Science. 2004;304:1926–1929. - PubMed
- Buzsáki G. Rhythms of the Brai. Oxford: Oxford Univ Press; 2006.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials