An efficient pseudomedian filter for tiling microrrays - PubMed (original) (raw)
An efficient pseudomedian filter for tiling microrrays
Thomas E Royce et al. BMC Bioinformatics. 2007.
Abstract
Background: Tiling microarrays are becoming an essential technology in the functional genomics toolbox. They have been applied to the tasks of novel transcript identification, elucidation of transcription factor binding sites, detection of methylated DNA and several other applications in several model organisms. These experiments are being conducted at increasingly finer resolutions as the microarray technology enjoys increasingly greater feature densities. The increased densities naturally lead to increased data analysis requirements. Specifically, the most widely employed algorithm for tiling array analysis involves smoothing observed signals by computing pseudomedians within sliding windows, a O(n2logn) calculation in each window. This poor time complexity is an issue for tiling array analysis and could prove to be a real bottleneck as tiling microarray experiments become grander in scope and finer in resolution.
Results: We therefore implemented Monahan's HLQEST algorithm that reduces the runtime complexity for computing the pseudomedian of n numbers to O(nlogn) from O(n2logn). For a representative tiling microarray dataset, this modification reduced the smoothing procedure's runtime by nearly 90%. We then leveraged the fact that elements within sliding windows remain largely unchanged in overlapping windows (as one slides across genomic space) to further reduce computation by an additional 43%. This was achieved by the application of skip lists to maintaining a sorted list of values from window to window. This sorted list could be maintained with simple O(log n) inserts and deletes. We illustrate the favorable scaling properties of our algorithms with both time complexity analysis and benchmarking on synthetic datasets.
Conclusion: Tiling microarray analyses that rely upon a sliding window pseudomedian calculation can require many hours of computation. We have eased this requirement significantly by implementing efficient algorithms that scale well with genomic feature density. This result not only speeds the current standard analyses, but also makes possible ones where many iterations of the filter may be required, such as might be required in a bootstrap or parameter estimation setting. Source code and executables are available at http://tiling.gersteinlab.org/pseudomedian/.
Figures
Figure 1
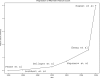
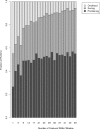
Number of features per Affymetrix brand microarray. Example studies' [1; 13–17] feature count are plotted as a function of their publication year.
Figure 2
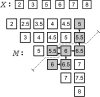
Computation of sliding window pseudomedianutilizing a 115 bp bandwidth. Raw signals are depicted in (A) along with their genomic coordinates (B). Pseudomedians are computed in a sliding window (C). As an example, (D) tabulates all 28 pairwise average in the window centered at position 1,250. The averages are sorted in (E) from which their median can be computed (F). The median of pairwise averages is also called the pseudomedian.
Figure 3
Pseudocode for the pseudomedian algorithm. For illustration purposes, this pseudocode assumes no ties in X.
Figure 4
Partitioning the pairwise means in linear time. A partition is indicated by a dotted line such that all elements above and to the left of the line are strictly less than six. The pairwise averages that are required to be computed for determining the partition are indicated by the path. Specifically, imagine that the current best guess at the pseudomedian is six – that is, we now want to divide S0 into those averages less than six and those greater than or equal to six. We start at the top and right of the matrix and encounter a value of 5. This is less than six so we move down one row. Again, we encounter a value, 5.5, that is less than six so we move down one more row. Note that we now know every element in these previous two rows are less than our partitioning element and that we determined this to be so by computing just two pairwise averages. Returning to the partitioning, we next encounter the value 6.5 which is greater than six, so we scan the row to the left until we find the first element, 5.5, which is less than our partitioning element. When this occurs, we move down a row from six, encounter 6.5, move left, find the value six and reach the diagonal, which completes the partitioning. Importantly, we reached this diagonal by computing only seven pairwise averages. The facilitating requirement of the input data is that it is sorted. This is the partitioning technique implemented in Monahan's algorithm.
Figure 5
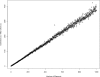
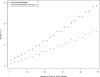
Observed runtime differences between computing the pseudomedian from its definition and by following Monahan's algorithm. On the _x_-axis is the number of randomly generated numbers for which the pseudomedian was desired. The _y_-axis is the result of dividing the definition's runtime by Monahan's runtime on the same set of values. The ratio scales linearly with number of elements as predicted from theory. The definition requires a O(n_2log_n) computation whereas Monahan's algorithm needs just O(n_log_n) computing time; we therefore expect a linear increase in their runtime ratio as n increases, and this is what we observe.
Figure 6
Linked list (A) and skip list (B). The skip list contains nodes with a variable number of forward pointers. A node's level is the same as the number of forward pointers it has. Insertion and deletion into the linked list requires a simple traversal of the list, requiring O(n) time. Insertion and deletion into/from the skip list can make use of short-cuts provided by the structure. For example, to insert '30' into (B), one would start at the node having value '1', skip ahead to the node holding '9', skip ahead to '13' and then to '29' before encountering '41', which is greater than the value to insert. The traversal would then visit the node having '37' and finally insert between '29' and '37'. Such an operation can be shown to have O(n_log_n) expected time.
Figure 7
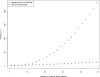
Runtimes of the pseudomedian smoothing algorithms over a one million element dataset. Times are plotted for the definition-derived implementation and for the Monahan modification as a function of feature count within the sliding window.
Figure 8
Fractional runtimes for the Monahan-modified pseudomedian filter. 'Sorting' refers to time spent sorting values within each window, 'Partitioning' refers to time spent searching for the pseudomedian, and 'Overhead' is the remainder of runtime within the filter.
Figure 9
Runtimes for pseudomedian smoothing using the Monahan modification with and without skip list.
Similar articles
- Assessing the need for sequence-based normalization in tiling microarray experiments.
Royce TE, Rozowsky JS, Gerstein MB. Royce TE, et al. Bioinformatics. 2007 Apr 15;23(8):988-97. doi: 10.1093/bioinformatics/btm052. Epub 2007 Mar 25. Bioinformatics. 2007. PMID: 17387113 - Custom design and analysis of high-density oligonucleotide bacterial tiling microarrays.
Thomassen GO, Rowe AD, Lagesen K, Lindvall JM, Rognes T. Thomassen GO, et al. PLoS One. 2009 Jun 17;4(6):e5943. doi: 10.1371/journal.pone.0005943. PLoS One. 2009. PMID: 19536279 Free PMC article. - A supervised hidden markov model framework for efficiently segmenting tiling array data in transcriptional and chIP-chip experiments: systematically incorporating validated biological knowledge.
Du J, Rozowsky JS, Korbel JO, Zhang ZD, Royce TE, Schultz MH, Snyder M, Gerstein M. Du J, et al. Bioinformatics. 2006 Dec 15;22(24):3016-24. doi: 10.1093/bioinformatics/btl515. Epub 2006 Oct 12. Bioinformatics. 2006. PMID: 17038339 - Issues in the analysis of oligonucleotide tiling microarrays for transcript mapping.
Royce TE, Rozowsky JS, Bertone P, Samanta M, Stolc V, Weissman S, Snyder M, Gerstein M. Royce TE, et al. Trends Genet. 2005 Aug;21(8):466-75. doi: 10.1016/j.tig.2005.06.007. Trends Genet. 2005. PMID: 15979196 Free PMC article. Review. - Applications of DNA tiling arrays to experimental genome annotation and regulatory pathway discovery.
Bertone P, Gerstein M, Snyder M. Bertone P, et al. Chromosome Res. 2005;13(3):259-74. doi: 10.1007/s10577-005-2165-0. Chromosome Res. 2005. PMID: 15868420 Review.
Cited by
- Identification of novel non-coding small RNAs from Streptococcus pneumoniae TIGR4 using high-resolution genome tiling arrays.
Kumar R, Shah P, Swiatlo E, Burgess SC, Lawrence ML, Nanduri B. Kumar R, et al. BMC Genomics. 2010 Jun 3;11:350. doi: 10.1186/1471-2164-11-350. BMC Genomics. 2010. PMID: 20525227 Free PMC article. - Lactase nonpersistence is directed by DNA-variation-dependent epigenetic aging.
Labrie V, Buske OJ, Oh E, Jeremian R, Ptak C, Gasiūnas G, Maleckas A, Petereit R, Žvirbliene A, Adamonis K, Kriukienė E, Koncevičius K, Gordevičius J, Nair A, Zhang A, Ebrahimi S, Oh G, Šikšnys V, Kupčinskas L, Brudno M, Petronis A. Labrie V, et al. Nat Struct Mol Biol. 2016 Jun;23(6):566-73. doi: 10.1038/nsmb.3227. Epub 2016 May 9. Nat Struct Mol Biol. 2016. PMID: 27159559 Free PMC article. - Wavelet-based detection of transcriptional activity on a novel Staphylococcus aureus tiling microarray.
Segura V, Toledo-Arana A, Uzqueda M, Lasa I, Muñoz-Barrutia A. Segura V, et al. BMC Bioinformatics. 2012 Sep 5;13:222. doi: 10.1186/1471-2105-13-222. BMC Bioinformatics. 2012. PMID: 22950634 Free PMC article. - Analysis of the regulated transcriptome of Neisseria meningitidis in human blood using a tiling array.
Del Tordello E, Bottini S, Muzzi A, Serruto D. Del Tordello E, et al. J Bacteriol. 2012 Nov;194(22):6217-32. doi: 10.1128/JB.01055-12. Epub 2012 Sep 14. J Bacteriol. 2012. PMID: 22984255 Free PMC article. - Active promoters and insulators are marked by the centrosomal protein 190.
Bartkuhn M, Straub T, Herold M, Herrmann M, Rathke C, Saumweber H, Gilfillan GD, Becker PB, Renkawitz R. Bartkuhn M, et al. EMBO J. 2009 Apr 8;28(7):877-88. doi: 10.1038/emboj.2009.34. Epub 2009 Feb 19. EMBO J. 2009. PMID: 19229299 Free PMC article.
References
Publication types
MeSH terms
Grants and funding
- 5P01HL063357-08/HL/NHLBI NIH HHS/United States
- P50 HG02357-01/HG/NHGRI NIH HHS/United States
- P01 HL063357/HL/NHLBI NIH HHS/United States
- P50 HG02357-0/HG/NHGRI NIH HHS/United States
- P50 HG002357/HG/NHGRI NIH HHS/United States
LinkOut - more resources
Full Text Sources
Molecular Biology Databases