Assessing the significance of conserved genomic aberrations using high resolution genomic microarrays - PubMed (original) (raw)
Comparative Study
Assessing the significance of conserved genomic aberrations using high resolution genomic microarrays
Mitchell Guttman et al. PLoS Genet. 2007 Aug.
Abstract
Genomic aberrations recurrent in a particular cancer type can be important prognostic markers for tumor progression. Typically in early tumorigenesis, cells incur a breakdown of the DNA replication machinery that results in an accumulation of genomic aberrations in the form of duplications, deletions, translocations, and other genomic alterations. Microarray methods allow for finer mapping of these aberrations than has previously been possible; however, data processing and analysis methods have not taken full advantage of this higher resolution. Attention has primarily been given to analysis on the single sample level, where multiple adjacent probes are necessarily used as replicates for the local region containing their target sequences. However, regions of concordant aberration can be short enough to be detected by only one, or very few, array elements. We describe a method called Multiple Sample Analysis for assessing the significance of concordant genomic aberrations across multiple experiments that does not require a-priori definition of aberration calls for each sample. If there are multiple samples, representing a class, then by exploiting the replication across samples our method can detect concordant aberrations at much higher resolution than can be derived from current single sample approaches. Additionally, this method provides a meaningful approach to addressing population-based questions such as determining important regions for a cancer subtype of interest or determining regions of copy number variation in a population. Multiple Sample Analysis also provides single sample aberration calls in the locations of significant concordance, producing high resolution calls per sample, in concordant regions. The approach is demonstrated on a dataset representing a challenging but important resource: breast tumors that have been formalin-fixed, paraffin-embedded, archived, and subsequently UV-laser capture microdissected and hybridized to two-channel BAC arrays using an amplification protocol. We demonstrate the accurate detection on simulated data, and on real datasets involving known regions of aberration within subtypes of breast cancer at a resolution consistent with that of the array. Similarly, we apply our method to previously published datasets, including a 250K SNP array, and verify known results as well as detect novel regions of concordant aberration. The algorithm has been fully implemented and tested and is freely available as a Java application at http://www.cbil.upenn.edu/MSA.
Conflict of interest statement
Competing interests. The authors have declared that no competing interests exist.
Figures
Figure 1. Illustration of Key Terms Used in the Description of the Analytical Method
(A) The footprint is defined for a given stack as the vertical projection on the genome of all overlapping intervals. The footprint measures the tightness of the overlapping intervals within a given stack. The frequency measures the number of overlapping intervals over a given location. These two metrics are sensitive to different effects, as a region can have the same frequency but different footprints, such as Region 1 and Region 2, which share a frequency but have different footprints. (B) A stack contains substacks of sizes 2, …, k (the number of intervals in a given stack). An example of a stack and its most significant substack of size three is shown. (C) Sample permutations are illustrated on data where little is aberrant to data where most of the genome is aberrant. A given interval is permuted by randomly placing an interval in the genome rather than breaking up the positions within an interval. Each sample is permuted independently.
Figure 2. Calculating _p_-Values from Raw Data
This figure illustrates how _p_-values are computed for the frequency statistic and the footprint statistic. The example tracks the frequency score but the argument is analogous for the footprint. We first begin with the raw data and calculate a score for each position. We then permute the data computing a maximum score for each permutation. We repeat the permutations n times, generating a distribution of the maximum observed score for each permutation. We then compare the score for each position on the genome to the distribution of the maximum score to compute multiple testing corrected _p_-values for each location.
Figure 3. Illustrates How the Footprint Can Identify Regions That the Frequency Misses
The starred region has a frequency that occurs under the permutation model frequently (frequency p = 1), yet the structure suggests a true aberration is present. The footprint statistic identifies this aberration as significant. This also illustrates the dependency between the footprint and frequency. Regions identified by the frequency are also identified by the footprint plus additional regions. The blue area tracks –log_(p)_ for the frequency. The green area tracks –log(p) for the footprint. The gray dotted lines indicate different significance levels.
Figure 4. Run Time of the STAC Algorithm
The time needed to run the STAC algorithm based on the original implementation and our new implementation. (A) Plots the run time as the length of the genome increases. (B) Plots the run time as the number of samples is increased. The numbers do not represent a typical dataset but rather a situation where every profile contains many aberrant intervals. For most real datasets the run time is significantly faster.
Figure 5. Example of the Multiple Sampling Approach on Neuroblastoma Chromosome 2 Data
(A) The distribution of aberrations is plotted versus the threshold cutoff of the log ratio for each sample. The red plot represents the percent aberration of loss, green is gain, and blue is the total percent aberration at a cutoff. (B) An image of the gains and losses called at three cutoffs is shown along with the log ratio used to determine gain and loss calls and the average percent aberration at that cutoff.
Figure 6. STAC Confidences for the Three Most Extreme MSA Test Values
This illustrates, on real data, that one cutoff value that reveals signal in one region can obscure real signal in other regions. (A) At a high cutoff it is possible to find tight concordance across positions 117–119 Mb and 190–191 Mb. (B) A middle cutoff preserves tight concordance at 117–119 Mb but loses 190–191 Mb and picks up additional regions such as 175–180 Mb. (C) At the lowest cutoff, the aberration at positions 117–119 Mb and at 175–180 Mb are obscured by noise. However, a new region at 181–184 Mb is detected. The height of the bar corresponds to the confidence level (1 − p). Dark gray bars are significant with p < 0.05.
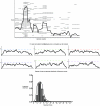
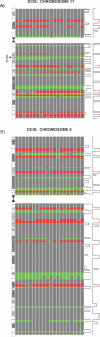
Figure 7. Concordant Aberrations on Chromosomes 8 and 17 in DCIS
(A) Copy number change for DCIS samples. No change (grey), deletion (red), or gain (green) are indicated. Only significant aberrations are visualized. ERBB2 amplification on Chromosome 17 across 20 DCIS samples is indicated. The aberration is localized to an approximately 1-Mb region across the samples. The line graph on the right tracks the confidence at each location, where regions of significant gain are indicated in green and significant loss are indicated in red. (B) Chromosome 8 across 20 DCIS samples. A large number of losses are detected on the p arm as well as the centromeric side of the q arm, while the telomeric end of the q arm contains many gains. These general patterns are interrupted by gains on the p arm and losses on the q arm that are detected with high confidence across multiple samples.
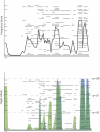
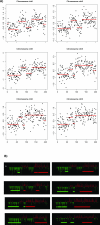
Figure 8. Comparison of Two Single Sample Methods on Chromosome 8 for DCIS
(A) DNAcopy (CBS) indicates gross level aberration. On most samples, CBS finds a large loss on the p arm and gain on the q arm. Additionally, on some samples CBS finds a large deletion on the q arm near the centromere. The _y-_axis represents the log ratio of the sample, the _x-_axis represents the genomic position, and the red lines represent the average copy number for each segment. (B) ChARM similarly finds gross level aberration including loss of the p arm and gain of the q arm. (red, gain and green, loss). ChARM misses the amplification of MYC in many samples, and in a few samples detects the amplification as a contiguous segment covering the entire q arm. The _y-_axis represents the log2(T/R) ratio of the sample and the _x-_axis represents the genomic position of the probe. Red boxes signify significant gain segments, green boxes signify significant loss segments, and the height of the bars represents the log ratio.
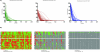
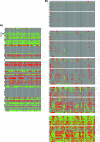
Figure 9. MSA Analysis of Neuroblastoma Dataset for Chromosome 2
(A) The merged view combines results from all cutoff values used. In the merged view, only the concordant aberration has been retained. All noise and nonconcordant signal has been filtered out for a clear visual representation of the concordant aberration and the contributing samples. (B) Individual views indicate results for five of the MSA test values along with their significance at each value.
Figure 10. CBS Algorithm Combined with the MSA Approach
The CBS algorithm was applied to segment the data and MSA was run on the resulting segments to determine conserved aberrations. Various values of the parameter for calculation of the segments were used. (A) represents the data of Mosse et al. on Chromosome 2 for the parameter value α = 0.05 and applying MSA. (B) represents the data of Naylor et al. on Chromosome 17 for various values of the parameter (α) from 0.05 to no segmentation.
Figure 11. Underlying Model of the Simulated Data
(A) Illustrates how concordant and nonconcordant aberrations are placed in the data. White circles represent locations containing no aberrations. Black circles represent intervals of nonconcordant aberrations. Blue circles represent intervals of concordant aberrations. In the blue and black circles the indicator random variable would have a value of 1 and the white circles would have a value of 0. The underlying frequency controls the expected number of aberrant samples containing a given concordant aberration. All circles represent random variables with the noise distribution described in the text. (B) Shows the underlying model on real data. The technical noise is not shown; only aberration intervals placed in the data are shown. The blue boxes highlight the placed concordant aberration regions. All the parameters for the different images were identical with the exception of the λ parameter, which was varied from λ = 0, …, 50.
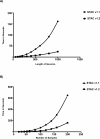
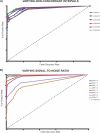
Figure 12. Simulated Data Accuracy Curves
Receiver operating characteristic–type curves are presented here as a measure of the accuracy of the MSA algorithm. The _x_-axis represents the FDR and the _y_-axis represents the TPR for each dataset. The graph was generated by determining the TPR and FDR at selected α values. If p < α, then the region is called significant, and if the region is known to be aberrant it is counted toward the TPR. If it is not aberrant, it is counted as a false positive. The values of α from which the plot was generated are plotted and the general curve is overlaid. (A) SNR is set equal to 1 for all comparison and the amount of nonconcordant signal is varied. Lambda is the mean nonconcordant signal in each profile. As we raise the amount of nonconcordant noise, we reduce the ability to detect true signal. (B) Lambda is fixed at a value of 10 and the SNR is varied to determine the effect of changing this parameter on detection of concordant aberrations. As we decrease the SNR, it becomes harder to detect concordant aberrations. At a SNR = 2 we detect 100% true positives with almost no false positives.
References
- Hanahan D, Weinberg RA. The hallmarks of cancer. Cell. 2000;100:57–70. - PubMed
- Buerger H, Otterbach F, Simon R, Poremba C, Diallo R, et al. Comparative genomic hybridization of ductal carcinoma in situ of the breast-evidence of multiple genetic pathways. J of Pathol. 1999;187:396–402. - PubMed
- Thor AD, Eng C, Devries S, Paterakos M, Watkin WG, et al. Invasive micropapillary carcinoma of the breast is associated with Chromosome 8 abnormalities detected by comparative genomic hybridization. Hum Pathol. 2002;6:628–631. - PubMed
- Pinkel D, Albertson DG. Array comparative genomic hybridization and its applications in cancer. Nat Genet Suppl. 2005;37:S11–S17. - PubMed
- Pinkel D, Albertson DG. Comparative genomic hybridization. Annu Rev Genomics Hum Genet. 2005;6:331–354. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases