Non-uniform plasma leakage affects local hematocrit and blood flow: implications for inflammation and tumor perfusion - PubMed (original) (raw)
Non-uniform plasma leakage affects local hematocrit and blood flow: implications for inflammation and tumor perfusion
Chenghai Sun et al. Ann Biomed Eng. 2007 Dec.
Abstract
Vessel leakiness is a hallmark of inflammation and cancer. In inflammation, plasma extravasation and leukocyte adhesion occur in a coordinated manner to enable the immune response, but also to maintain tissue perfusion. In tumors, similar mechanisms operate, but they are not well regulated. Therefore, blood perfusion in tumors is non-uniform, and delivery of blood-borne therapeutics is difficult. In order to analyze the interplay among plasma leakage, blood viscosity, and vessel geometry, we developed a mathematical model that explicitly includes blood cells, vessel branching, and focal leakage. The results show that local hemoconcentration due to plasma leakage can greatly increase the flow resistance in individual vascular segments, diverting flow to other regions. Similarly, leukocyte rolling can increase flow resistance by partially blocking flow. Vessel dilation can counter these effects, and likely occurs in inflammation to maintain blood flow. These results suggest that potential strategies for improving perfusion through tumor networks include (i) eliminating non-uniform plasma leakage, (ii) inhibiting leukocyte interactions, and (iii) preventing RBC aggregation in sluggish vessels. Normalization of tumor vessels by anti-angiogenic therapy may improve tumor perfusion via the first two mechanisms.
Figures
FIGURE 1
Model geometry and parameters. At top is an illustration of how the blood suspension is modeled. Red blood cells are represented as 2D capsules and the white blood cells are 2D disks (yellow). The leukocyte interacts with the wall through stochastic receptor–ligand interactions (illustrated at bottom right) and a non-specific repulsive force (_F_C). The leukocyte can interact with the surface when it gets closer than _H_C. The forces and torques of individual bonds are summed to get the total ligand force (_F_L) and torque (_T_L); these are then combined with the hydrodynamic force (_F_H) and the torque (_T_H) to calculate the total force on the leukocyte. Fluid particle velocities of a 2D lattice Boltzmann model with nine velocities are illustrated at bottom left.
FIG. 2
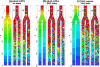
Representative snapshots of flow during the simulations. The columns represent (a) equal width, non-leaky daughter branches; (b) equal width branches, but the right-hand channel (RHC) leaks; (c) the RHC is 50% wider, and has the same leaks as case b. In each case, Subpanel I is the steady flow of plasma only (without any cells). Subpanel II shows the developed flow of RBCs for feeding hematocrit 0.35 at the inlet. Subpanel III shows the flow with both RBCs and WBCs included. Lattice size: 1000 × 150; one grid point is equal to 0.3 _μ_m. Total time of 0.9 s is normalized to 1, corresponding to 3 × 106 time-steps. The pressure coefficient (P = 2(p – _p_ex)/ρ _U_2, where _p_ex is pressure at the exit) field is represented by the color gradient and the velocity field is represented by small arrows.
FIGURE 3
Velocity evolution in each segment. For the simulations with cells, the initial condition is the flow-pressure distribution for plasma only (i.e., panel I from Fig. 2). Here we show the changes in velocity that occur as RBCs (top row) or RBCs and WBCs (bottom row) enter the system. Velocities have been averaged across the channel width, and the inlet hematocrit is 0.35. The geometries of Cases a, b, and c are illustrated to the right of corresponding velocity plots; the colored lines in these diagrams correspond to the locations of the velocities in the plots (i.e., blue is at the inlet, orange is at the entrance to the left-hand branch, etc.). In (b) and (c), the leaking velocity is depicted by the gray line. The initial steady-state velocity distribution is disturbed as cells fill the system; in (b) and (c), plasma leakage causes dramatic drifts in the velocity distributions.
FIGURE 4
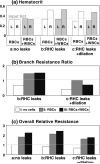
Summary of hematocrit (Panel a), overall resistance (Panel b) relative to that of plasma flow in a non-leaky vessel (simulation a-I in Fig. 2), and resistance ratio of right branch to left branch (Panel c). Groups a, b, and c represent the Cases a, b, and c shown in Fig. 2. I, II, and III indicate the simulations I, II, and III in Fig. 2. L and R denote the left and right branch, respectively. The values for II and III are the temporal averages over dimensionless time interval from 2/3 to 1.
Similar articles
- Determinants of tumor blood flow: a review.
Jain RK. Jain RK. Cancer Res. 1988 May 15;48(10):2641-58. Cancer Res. 1988. PMID: 3282647 Review. - Microvascular blood flow resistance: Role of red blood cell migration and dispersion.
Katanov D, Gompper G, Fedosov DA. Katanov D, et al. Microvasc Res. 2015 May;99:57-66. doi: 10.1016/j.mvr.2015.02.006. Epub 2015 Feb 25. Microvasc Res. 2015. PMID: 25724979 - Viscous resistance to blood flow in solid tumors: effect of hematocrit on intratumor blood viscosity.
Sevick EM, Jain RK. Sevick EM, et al. Cancer Res. 1989 Jul 1;49(13):3513-9. Cancer Res. 1989. PMID: 2731173 - Study of tumor blood perfusion and its variation due to vascular normalization by anti-angiogenic therapy based on 3D angiogenic microvasculature.
Wu J, Long Q, Xu S, Padhani AR. Wu J, et al. J Biomech. 2009 Apr 16;42(6):712-21. doi: 10.1016/j.jbiomech.2009.01.009. Epub 2009 Mar 5. J Biomech. 2009. PMID: 19268290 - New trends in clinical hemorheology: an introduction to the concept of the hemorheological profile.
Stoltz JF, Donner M. Stoltz JF, et al. Schweiz Med Wochenschr Suppl. 1991;43:41-9. Schweiz Med Wochenschr Suppl. 1991. PMID: 1843037 Review.
Cited by
- Blood cell interactions and segregation in flow.
Munn LL, Dupin MM. Munn LL, et al. Ann Biomed Eng. 2008 Apr;36(4):534-44. doi: 10.1007/s10439-007-9429-0. Epub 2008 Jan 11. Ann Biomed Eng. 2008. PMID: 18188702 Free PMC article. Review. - Cancer and inflammation.
Munn LL. Munn LL. Wiley Interdiscip Rev Syst Biol Med. 2017 Mar;9(2):10.1002/wsbm.1370. doi: 10.1002/wsbm.1370. Epub 2016 Dec 12. Wiley Interdiscip Rev Syst Biol Med. 2017. PMID: 27943646 Free PMC article. Review. - Modulating the Tumor Microenvironment to Enhance Tumor Nanomedicine Delivery.
Zhang B, Hu Y, Pang Z. Zhang B, et al. Front Pharmacol. 2017 Dec 22;8:952. doi: 10.3389/fphar.2017.00952. eCollection 2017. Front Pharmacol. 2017. PMID: 29311946 Free PMC article. Review. - [Contrast-enhanced ultrasound in the diagnostic workup of lymph nodes].
Weskott HP. Weskott HP. Radiologe. 2018 Jun;58(6):563-571. doi: 10.1007/s00117-018-0389-1. Radiologe. 2018. PMID: 29728746 Review. German. - The interplay between physical cues and mechanosensitive ion channels in cancer metastasis.
Bera K, Kiepas A, Zhang Y, Sun SX, Konstantopoulos K. Bera K, et al. Front Cell Dev Biol. 2022 Sep 7;10:954099. doi: 10.3389/fcell.2022.954099. eCollection 2022. Front Cell Dev Biol. 2022. PMID: 36158191 Free PMC article. Review.
References
- Baffert F, Le T, Thurston G, McDonald DM. Angiopoietin-1 decreases plasma leakage by reducing number and size of endothelial gaps in venules. Am. J. Physiol. Heart Circ. Physiol. 2006;290:H107–H118. - PubMed
- Baish JW, Netti PA, Jain RK. Transmural coupling of fluid flow in microcirculatory network and interstitium in tumors. Microvasc. Res. 1997;53:128–141. - PubMed
- Baxter LT, Jain RK. Vascular permeability and interstitial diffusion in superfused tissues: a two-dimensional model. Microvasc. Res. 1988;36:108–115. - PubMed
- Bishop JJ, Popel AS, Intaglietta M, Johnson PC. Effects of erythrocyte aggregation and venous network geometry on red blood cell axial migration. Am. J. Physiol. Heart Circ. Physiol. 2001;281:H939–H950. - PubMed
- Campbell RB, Fukumura D, Brown EB, Mazzola LM, Izumi Y, Jain RK, Torchilin VP, Munn LL. Cationic charge determines the distribution of liposomes between the vascular and extravascular compartments of tumors. Cancer Res. 2002;62:6831–6836. - PubMed
Publication types
MeSH terms
Grants and funding
- R01 HL064240-06/HL/NHLBI NIH HHS/United States
- R01 HL064240-07/HL/NHLBI NIH HHS/United States
- R01 HL064240-08/HL/NHLBI NIH HHS/United States
- R01 HL064240-03/HL/NHLBI NIH HHS/United States
- P01 CA080124/CA/NCI NIH HHS/United States
- R01 HL064240/HL/NHLBI NIH HHS/United States
- R01 HL64240/HL/NHLBI NIH HHS/United States
- P01 CA080124-080006/CA/NCI NIH HHS/United States
- R01 HL064240-04/HL/NHLBI NIH HHS/United States
- R01 HL064240-05/HL/NHLBI NIH HHS/United States
LinkOut - more resources
Full Text Sources
Medical