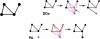Using likelihood-free inference to compare evolutionary dynamics of the protein networks of H. pylori and P. falciparum - PubMed (original) (raw)
Comparative Study
Using likelihood-free inference to compare evolutionary dynamics of the protein networks of H. pylori and P. falciparum
Oliver Ratmann et al. PLoS Comput Biol. 2007 Nov.
Abstract
Gene duplication with subsequent interaction divergence is one of the primary driving forces in the evolution of genetic systems. Yet little is known about the precise mechanisms and the role of duplication divergence in the evolution of protein networks from the prokaryote and eukaryote domains. We developed a novel, model-based approach for Bayesian inference on biological network data that centres on approximate Bayesian computation, or likelihood-free inference. Instead of computing the intractable likelihood of the protein network topology, our method summarizes key features of the network and, based on these, uses a MCMC algorithm to approximate the posterior distribution of the model parameters. This allowed us to reliably fit a flexible mixture model that captures hallmarks of evolution by gene duplication and subfunctionalization to protein interaction network data of Helicobacter pylori and Plasmodium falciparum. The 80% credible intervals for the duplication-divergence component are [0.64, 0.98] for H. pylori and [0.87, 0.99] for P. falciparum. The remaining parameter estimates are not inconsistent with sequence data. An extensive sensitivity analysis showed that incompleteness of PIN data does not largely affect the analysis of models of protein network evolution, and that the degree sequence alone barely captures the evolutionary footprints of protein networks relative to other statistics. Our likelihood-free inference approach enables a fully Bayesian analysis of a complex and highly stochastic system that is otherwise intractable at present. Modelling the evolutionary history of PIN data, it transpires that only the simultaneous analysis of several global aspects of protein networks enables credible and consistent inference to be made from available datasets. Our results indicate that gene duplication has played a larger part in the network evolution of the eukaryote than in the prokaryote, and suggests that single gene duplications with immediate divergence alone may explain more than 60% of biological network data in both domains.
Conflict of interest statement
Competing interests. The authors have declared that no competing interests exist.
Figures
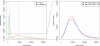
Figure 1. Choosing Appropriate Summaries with a Characterization of Genuine Change
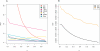
The standardized mean gradient smd is plotted as a function of α. Fifty networks corresponding to H. pylori (grown to 1,500 nodes and subsampled to 675) were generated as described in the text with θ ∈ [0.1, 0.7] × [0, 0.5] × [0.1, 0.6] in steps of 0.025; all mean summaries were computed for each θ. The marginal smd(α) is plotted for (A) summary statistics and (B) summary distributions. Together with cv in Figure S4, smd characterizes the sensitivity and variability of single summary statistics on simulated data. All summaries except ND have smd not close to zero, whereas TRIA, FRAG, and CC are extremely variable. Results for the other two parameters are very similar (unpublished data). The range of CC was truncated for display purposes.
Figure 2. Comparing Distance Functions on a Set of Summaries.
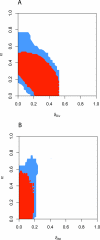
To compare different distance functions on sets of summaries, we analyzed the two-dimensional posterior support of θ for the H. pylori PIN dataset. (A) α versus δ Div and (B) α versus δ Att. Using LFI with the set of summaries WR + DIA + CC +  + FRAG, we recorded after burn-in the accepted parameters when each mean summary differed from the observed summary within the respective thresholds ɛk,min (d ∩, red), and when the sum of these differences did not exceed the sum Σ_kɛk_,min of these thresholds (d Σ, blue). In both cases, we used an average of shifted histograms to estimate the two-dimensional posterior support. When using d ∩, the posterior support was more restricted, prompting us to use d ∩ in LFI.
+ FRAG, we recorded after burn-in the accepted parameters when each mean summary differed from the observed summary within the respective thresholds ɛk,min (d ∩, red), and when the sum of these differences did not exceed the sum Σ_kɛk_,min of these thresholds (d Σ, blue). In both cases, we used an average of shifted histograms to estimate the two-dimensional posterior support. When using d ∩, the posterior support was more restricted, prompting us to use d ∩ in LFI.
Figure 3. LFI on the H. pylori PIN
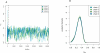
For the H. pylori PIN dataset, four MCMC chains were run for 75,000 iterations according to LFI based on the summaries WR + DIA + CC +  + FRAG. (A) The four chains for the parameter δ Div ∈ [0,1] over the first 30,000 iterations. During burn-in, the chains moved quickly from overdispersed starting values and converged toward the same narrow support. Before iteration 800 (vertical line), ɛ was cooled to the minimal temperature; thereafter, accepted parameters were recorded, representing samples from the approximate posterior (Equation 4). (B) Accepted parameters after convergence were pooled over the four chains and used to estimate the posterior density. For δ Div, the marginal posterior is displayed (black line); in addition, posteriors were calculated for each chain and are overlaid, showing that the four sets of posterior samples overlapped well.
+ FRAG. (A) The four chains for the parameter δ Div ∈ [0,1] over the first 30,000 iterations. During burn-in, the chains moved quickly from overdispersed starting values and converged toward the same narrow support. Before iteration 800 (vertical line), ɛ was cooled to the minimal temperature; thereafter, accepted parameters were recorded, representing samples from the approximate posterior (Equation 4). (B) Accepted parameters after convergence were pooled over the four chains and used to estimate the posterior density. For δ Div, the marginal posterior is displayed (black line); in addition, posteriors were calculated for each chain and are overlaid, showing that the four sets of posterior samples overlapped well.
Figure 4. Comparison of Inference with LFI Using One versus Four Summaries for the H. pylori PIN Data
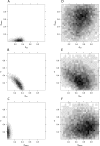
(A–C) The 2D histograms of the posterior parameters to the H. pylori PIN dataset, obtained from LFI based on WR + DIA + CC +  + FRAG. Posterior mass clearly centers on a tight cloud in parameter space. (D–F) For comparison, we ran LFI based on ND alone, adjusted to yield a similar empirical acceptance probability. Although ɛ min could be chosen stringently, the 2D histograms are diffuse. The regions of highest posterior density of LFI using ND are inconsistent with those of LFI using WR + DIA + CC +
+ FRAG. Posterior mass clearly centers on a tight cloud in parameter space. (D–F) For comparison, we ran LFI based on ND alone, adjusted to yield a similar empirical acceptance probability. Although ɛ min could be chosen stringently, the 2D histograms are diffuse. The regions of highest posterior density of LFI using ND are inconsistent with those of LFI using WR + DIA + CC +  + FRAG.
+ FRAG.
Figure 5. Posterior Densities of the Predicted Network Size for the Complete H. pylori and P. falciparum PINs with LFI Based on WR + DIA + CC + + FRAG
(Left) posterior modes (5,636 and 43,835, dashed line and dot-dashed line, respectively) were consistent with the estimator presented in [22] (6,082 and 45,940, respectively; black horizontal lines). The 80% credible interval of the predicted network size for the H. pylori PIN was [2,915, ,536], and the one for the P. falciparum PIN was [18,689, 84,205], illustrating the high variability in the posterior estimate, in particular when the sampling fraction is low (ρ = 0.45 and 0.24, respectively). (Right) for the P. falciparum PIN, LFI was repeated using the same set of summaries at relaxed threshold values as indicated in the legend. For display purposes, the _y_-axis was magnified relative to the left figure. As expected, larger thresholds yielded less-confident approximations (Equation 4).
Figure 6. The Effect of Increasing Incompleteness on Summaries
For increasingly incomplete PIN datasets of P. falciparum, four MCMC chains were run for 75,000 iterations according to LFI based on WR + DIA + CC +  + FRAG. We present the marginal posterior densities of the mixture parameter α for two PIN datasets: (A) LFI on four random subsets of order 900 for ρ = 0.17 of the P. falciparum PIN dataset (each corresponding to one Markov chain), and (B) LFI on the full P. falciparum PIN dataset for ρ = 0.24. The chains were tempered to the minimal threshold values before iteration 800, and converged well onto posterior support. After iteration 800, the chains were taken to represent samples from the posterior, which produced the displayed kernel density estimate. Although LFI is sensitive to the randomly withheld data points, the estimated posteriors of each chain in (A) largely agree with the posterior on the full dataset. This indicates that randomly omitting 500 proteins does not seriously affect algorithm LFI.
+ FRAG. We present the marginal posterior densities of the mixture parameter α for two PIN datasets: (A) LFI on four random subsets of order 900 for ρ = 0.17 of the P. falciparum PIN dataset (each corresponding to one Markov chain), and (B) LFI on the full P. falciparum PIN dataset for ρ = 0.24. The chains were tempered to the minimal threshold values before iteration 800, and converged well onto posterior support. After iteration 800, the chains were taken to represent samples from the posterior, which produced the displayed kernel density estimate. Although LFI is sensitive to the randomly withheld data points, the estimated posteriors of each chain in (A) largely agree with the posterior on the full dataset. This indicates that randomly omitting 500 proteins does not seriously affect algorithm LFI.
Figure 7. Randomly Growing Graphs
Similar articles
- Model criticism based on likelihood-free inference, with an application to protein network evolution.
Ratmann O, Andrieu C, Wiuf C, Richardson S. Ratmann O, et al. Proc Natl Acad Sci U S A. 2009 Jun 30;106(26):10576-81. doi: 10.1073/pnas.0807882106. Epub 2009 Jun 12. Proc Natl Acad Sci U S A. 2009. PMID: 19525398 Free PMC article. - Modeling protein network evolution under genome duplication and domain shuffling.
Evlampiev K, Isambert H. Evlampiev K, et al. BMC Syst Biol. 2007 Nov 13;1:49. doi: 10.1186/1752-0509-1-49. BMC Syst Biol. 2007. PMID: 17999763 Free PMC article. - Conservation and topology of protein interaction networks under duplication-divergence evolution.
Evlampiev K, Isambert H. Evlampiev K, et al. Proc Natl Acad Sci U S A. 2008 Jul 22;105(29):9863-8. doi: 10.1073/pnas.0804119105. Epub 2008 Jul 16. Proc Natl Acad Sci U S A. 2008. PMID: 18632555 Free PMC article. - Evolutionary divergence of Plasmodium falciparum: sequences, protein-protein interactions, pathways and processes.
Tyagi N, Swapna LS, Mohanty S, Agarwal G, Gowri VS, Anamika K, Priya ML, Krishnadev O, Srinivasan N. Tyagi N, et al. Infect Disord Drug Targets. 2009 Jun;9(3):257-71. doi: 10.2174/1871526510909030257. Infect Disord Drug Targets. 2009. PMID: 19519480 Review. - A practical guide to pseudo-marginal methods for computational inference in systems biology.
Warne DJ, Baker RE, Simpson MJ. Warne DJ, et al. J Theor Biol. 2020 Jul 7;496:110255. doi: 10.1016/j.jtbi.2020.110255. Epub 2020 Mar 26. J Theor Biol. 2020. PMID: 32223995 Review.
Cited by
- Approximate Bayesian Computation for Discrete Spaces.
Auzina IA, Tomczak JM. Auzina IA, et al. Entropy (Basel). 2021 Mar 6;23(3):312. doi: 10.3390/e23030312. Entropy (Basel). 2021. PMID: 33800743 Free PMC article. - A Bayesian approach to the evolution of metabolic networks on a phylogeny.
Mithani A, Preston GM, Hein J. Mithani A, et al. PLoS Comput Biol. 2010 Aug 5;6(8):e1000868. doi: 10.1371/journal.pcbi.1000868. PLoS Comput Biol. 2010. PMID: 20700467 Free PMC article. - Simulation-based Bayesian Analysis of Complex Data.
Marjoram P, Hamblin S, Foley B. Marjoram P, et al. Summer Comput Simul Conf (2015). 2015 Dec;47(10):176-183. Summer Comput Simul Conf (2015). 2015. PMID: 27840859 Free PMC article. - Model criticism based on likelihood-free inference, with an application to protein network evolution.
Ratmann O, Andrieu C, Wiuf C, Richardson S. Ratmann O, et al. Proc Natl Acad Sci U S A. 2009 Jun 30;106(26):10576-81. doi: 10.1073/pnas.0807882106. Epub 2009 Jun 12. Proc Natl Acad Sci U S A. 2009. PMID: 19525398 Free PMC article. - Adaptive importance sampling for network growth models.
Guetz AN, Holmes SP. Guetz AN, et al. Ann Oper Res. 2011 Sep;189(1):187-203. doi: 10.1007/s10479-010-0685-2. Ann Oper Res. 2011. PMID: 27182098 Free PMC article.
References
- Lynch M, Conery JS. The evolutionary fate and consequences of duplicate genes. Science. 2000;290:1151–1155. - PubMed
- Gough J, Karplus K, Hughey R, Chothia C. Assignment of homology to genome sequences using a library of hidden markov models that represent all proteins of known structure. J Mol Biol. 2001;313:14658–14663. - PubMed