Velvet: algorithms for de novo short read assembly using de Bruijn graphs - PubMed (original) (raw)

Velvet: algorithms for de novo short read assembly using de Bruijn graphs

Daniel R Zerbino et al. Genome Res. 2008 May.

Abstract

We have developed a new set of algorithms, collectively called "Velvet," to manipulate de Bruijn graphs for genomic sequence assembly. A de Bruijn graph is a compact representation based on short words (k-mers) that is ideal for high coverage, very short read (25-50 bp) data sets. Applying Velvet to very short reads and paired-ends information only, one can produce contigs of significant length, up to 50-kb N50 length in simulations of prokaryotic data and 3-kb N50 on simulated mammalian BACs. When applied to real Solexa data sets without read pairs, Velvet generated contigs of approximately 8 kb in a prokaryote and 2 kb in a mammalian BAC, in close agreement with our simulated results without read-pair information. Velvet represents a new approach to assembly that can leverage very short reads in combination with read pairs to produce useful assemblies.

PubMed Disclaimer

Figures

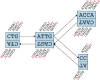
Figure 1.

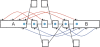
Figure 1.

Schematic representation of our implementation of the de Bruijn graph. Each node, represented by a single rectangle, represents a series of overlapping _k_-mers (in this case, k = 5), listed directly above or below. (Red) The last nucleotide of each _k_-mer. The sequence of those final nucleotides, copied in large letters in the rectangle, is the sequence of the node. The twin node, directly attached to the node, either below or above, represents the reverse series of reverse complement _k_-mers. Arcs are represented as arrows between nodes. The last _k_-mer of an arc’s origin overlaps with the first of its destination. Each arc has a symmetric arc. Note that the two nodes on the left could be merged into one without loss of information, because they form a chain.

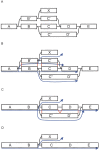
Figure 2.

Figure 2.

Example of Tour Bus error correction. (A) Original graph. (B) The search starts from A and spreads toward the right. The progression of the top path (through B′ and C′) is stopped because D was previously visited. The nucleotide sequences corresponding to the alternate paths B′C′ and BC are extracted from the graph, aligned, and compared. (C) The two paths are judged similar, so the longer one, B′C′, is merged into the shorter one, BC. The merging is directed by the alignment of the consensus sequences, indicated in red lines in B. Note that node X, which was connected to node B′, is now connected to node B. The search progresses, and the bottom path (through C′ and D′) arrives second in E. Once again, the corresponding paths, C′D′ and CD are compared. (D) CD and C′D′ are judged similar enough. The longer path is merged into the shorter one.

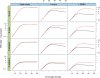
Figure 3.

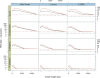
Figure 3.

Simulations of Tour Bus. The genome of E. coli and 5-Mb samples of DNA from three other species (S. cerevisiae, C. elegans, and H. sapiens, respectively) were used to generate 35-bp read sets of varying read depths (_X_-axis of each plot). We measured the contig length N50 (_Y_-axis, log scale) after tip-clipping (black curve) then after the subsequent bubble smoothing (red curve). In the first column are the results for perfect, error-free reads. In the second column, we inserted errors in the reads at a rate of 1%. In the third column, we generated a slightly variant genome from the original by inserting random SNPs at a rate of 1 in 500. The reads were then generated with errors from both variants, thus simulating a diploid assembly.

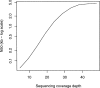
Figure 4.

Figure 4.

Effect of coverage on contig length with experimental Streptococcus data.

Figure 5.

Figure 5.

Breadcrumb algorithm. Two long contigs produced after error correction, A and B, are joined by several paired reads (red and blue arcs). The path between the two can be broken up because of a repeat internal to the connecting sequence, because of an overlap with a distinct part of the genome, or because of some unresolved errors. The small square nodes represent either nodes of the path between A and B, or other nodes of the graph connected to the former. Finding the exact path in the graph from A to B is not straightforward because of all the alternate paths that need to be explored. However, if we mark all the nodes that are paired up to either A or B (with a blue circle), we can define a subgraph much simpler to explore. Ideally, only a linear path connects both nodes.

Figure 6.

Figure 6.

Breadcrumb performance on simulated data sets. As in Figure 3, we sampled 5-Mb DNA sequences from four different species (E. coli, S. cerevisiae, C. elegans, and H. sapiens, respectively) and generated 50× read sets. The horizontal lines represent the N50 reached at the end of Tour Bus (see Fig. 3) (broken black line) and after applying a 4× coverage cutoff (broken red line). Note how the difference in N50 between the graph of perfect reads and that of erroneous reads is significantly reduced by this last cutoff. (Black curves) The results after the basic Breadcrumb algorithm; (red curves) the results after super-contigging.

Similar articles

Cited by

References

    1. Batzoglou S. Algorithmic challenges in mammalian genome sequence assembly. In: Dunn M., et al., editors. Encyclopedia of genomics, proteomics and bioinformatics. John Wiley and Sons; New York: 2005. Part 4.
    1. Batzoglou S., Jaffe D.B., Stanley K., Butler J., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Jaffe D.B., Stanley K., Butler J., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Stanley K., Butler J., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Butler J., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Gnerre S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Mauceli E., Berger B., Mesirov J.P., Lander E.S., Berger B., Mesirov J.P., Lander E.S., Mesirov J.P., Lander E.S., Lander E.S. ARACHNE: A whole genome shotgun assembler. Genome Res. 2002;12:177–189. - PMC - PubMed
    1. Bentley D.R. Whole-genome re-sequencing. Curr. Opin. Genet. Dev. 2006;16:545–552. - PubMed
    1. Bokhari S.H., Sauer J.R., Sauer J.R. A parallel graph decomposition algorithm for DNA sequencing with nanopores. Bioinformatics. 2005;21:889–896. - PubMed
    1. Chaisson M., Pevzner P.A., Tang H., Pevzner P.A., Tang H., Tang H. Fragment assembly with short reads. Bioinformatics. 2004;20:2067–2074. - PubMed

Publication types

MeSH terms

LinkOut - more resources