Feedback regulation of opposing enzymes generates robust, all-or-none bistable responses - PubMed (original) (raw)

Feedback regulation of opposing enzymes generates robust, all-or-none bistable responses

James E Ferrell Jr. Curr Biol. 2008.

No abstract available

PubMed Disclaimer

Figures

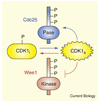
Figure 1

Schematic view of the reciprocal positive and double-negative feedback loops in the CDK1–Cdc25–Wee1 system.

Figure 2

Feedback regulation of opposing enzymes yields robust bistable responses. (A) No feedback loops. One enzyme activates A; a second inactivates it. The activation rate curve (blue) and the inactivation rate curve (red) intersect at a single point, which represents the stable steady state (SSS) of the system. (B) One feedback loop. We assume that A positively feeds back on its activator. The inactivation rate curve is unchanged (red), but now the activation rate rises and then falls as the activity of A increases (blue). If the rate constants and concentrations of the activator and inactivator are appropriately matched, the curves can intersect at three points. Two correspond to stable steady states (SSS) and one to an unstable steady state (USS). The dashed red lines depict the highest and lowest rate constants for the inactivation reaction compatible with bistability. (C) Two feedback loops. We assume that A activates its activator (blue curve) in a positive feedback loop, and inactivates its inactivator (red curve) in a negative feedback loop. The result is rate curves that are roughly mirror images of each other, and either curve can be stretched to a huge extent without eliminating the bistability. The equations upon which these plots are based are discussed qualitatively in the main text and are derived in the Supplemental Data, published with this article online.

Similar articles

• New pathways from PKA to the Cdc2/cyclin B complex in oocytes: Wee1B as a potential PKA substrate.
  Han SJ, Conti M. Han SJ, et al. Cell Cycle. 2006 Feb;5(3):227-31. doi: 10.4161/cc.5.3.2395. Epub 2006 Feb 8. Cell Cycle. 2006. PMID: 16418576 Review.
• PKA and CDC25B: at last connected.
  Schultz R. Schultz R. Cell Cycle. 2009 Feb 15;8(4):516-7. Epub 2009 Feb 15. Cell Cycle. 2009. PMID: 19221472 No abstract available.
• The xenopus Suc1/Cks protein promotes the phosphorylation of G(2)/M regulators.
  Patra D, Wang SX, Kumagai A, Dunphy WG. Patra D, et al. J Biol Chem. 1999 Dec 24;274(52):36839-42. doi: 10.1074/jbc.274.52.36839. J Biol Chem. 1999. PMID: 10601234
• Constant regulation of both the MPF amplification loop and the Greatwall-PP2A pathway is required for metaphase II arrest and correct entry into the first embryonic cell cycle.
  Lorca T, Bernis C, Vigneron S, Burgess A, Brioudes E, Labbé JC, Castro A. Lorca T, et al. J Cell Sci. 2010 Jul 1;123(Pt 13):2281-91. doi: 10.1242/jcs.064527. J Cell Sci. 2010. PMID: 20554897
• [Regulation of the cell cycle and checkpoint by SCF(beta-TrCP)].
  Kanemori Y, Sagata N. Kanemori Y, et al. Tanpakushitsu Kakusan Koso. 2006 Aug;51(10 Suppl):1386-90. Tanpakushitsu Kakusan Koso. 2006. PMID: 16922405 Review. Japanese. No abstract available.

Cited by

• Regulated protein kinases and phosphatases in cell cycle decisions.
  Novak B, Kapuy O, Domingo-Sananes MR, Tyson JJ. Novak B, et al. Curr Opin Cell Biol. 2010 Dec;22(6):801-8. doi: 10.1016/j.ceb.2010.07.001. Epub 2010 Aug 2. Curr Opin Cell Biol. 2010. PMID: 20678910 Free PMC article. Review.
• Stochastic modeling of B lymphocyte terminal differentiation and its suppression by dioxin.
  Zhang Q, Bhattacharya S, Kline DE, Crawford RB, Conolly RB, Thomas RS, Kaminski NE, Andersen ME. Zhang Q, et al. BMC Syst Biol. 2010 Apr 1;4:40. doi: 10.1186/1752-0509-4-40. BMC Syst Biol. 2010. PMID: 20359356 Free PMC article.
• Ultrasensitivity part III: cascades, bistable switches, and oscillators.
  Ferrell JE Jr, Ha SH. Ferrell JE Jr, et al. Trends Biochem Sci. 2014 Dec;39(12):612-8. doi: 10.1016/j.tibs.2014.10.002. Epub 2014 Nov 10. Trends Biochem Sci. 2014. PMID: 25456048 Free PMC article. Review.
• A genetic bistable switch utilizing nonlinear protein degradation.
  Huang D, Holtz WJ, Maharbiz MM. Huang D, et al. J Biol Eng. 2012 Jul 9;6(1):9. doi: 10.1186/1754-1611-6-9. J Biol Eng. 2012. PMID: 22776405 Free PMC article.
• Feedback loops shape cellular signals in space and time.
  Brandman O, Meyer T. Brandman O, et al. Science. 2008 Oct 17;322(5900):390-5. doi: 10.1126/science.1160617. Science. 2008. PMID: 18927383 Free PMC article. Review.

References

1. 1. Novick A, Wiener M. Enzyme induction as an all-or-none phenomenon. Proc. Natl. Acad. Sci. USA. 1957;43:553–566. - PMC - PubMed
2. 1. Monod J, Jacob F. General conclusions: teleonomic mechanisms in cellular metabolism, growth, and differentiation. Cold Spring Harbor Symp. Quant. Biol. 1961;26:389–401. - PubMed
3. 1. Griffith JS. Mathematics of cellular control processes. II. Positive feedback to one gene. J. Theor. Biol. 1968;20:209–216. - PubMed
4. 1. Ferrell JE. Self-perpetuating states in signal transduction: positive feedback, doublenegative feedback and bistability. Curr. Opin. Cell Biol. 2002;14:140–148. - PubMed
5. 1. Morgan DO. The Cell Cycle: Principles of Control. New Science Press, Ltd; 2006.

Publication types

MeSH terms

Substances

Grants and funding

• R01 GM061276-08/GM/NIGMS NIH HHS/United States
• R01 GM061276/GM/NIGMS NIH HHS/United States
• R01 GM061276-09A1/GM/NIGMS NIH HHS/United States
• GM61276/GM/NIGMS NIH HHS/United States
• R01 GM061276-07/GM/NIGMS NIH HHS/United States

LinkOut - more resources

• Full Text Sources

  • Elsevier Science
  • Europe PubMed Central
  • PubMed Central