Salt dependence of nucleic acid hairpin stability - PubMed (original) (raw)
Salt dependence of nucleic acid hairpin stability
Zhi-Jie Tan et al. Biophys J. 2008 Jul.
Abstract
Single-stranded junctions/loops are frequently occurring structural motifs in nucleic acid structures. Due to the polyanionic nature of the nucleic acid backbone, metal ions play a crucial role in the loop stability. Here we use the tightly bound ion theory, which can account for the possible ion correlation and ensemble (fluctuation) effects, to predict the ion-dependence of loop and stem-loop (hairpin) free energies. The predicted loop free energy is a function of the loop length, the loop end-to-end distance, and the ion (Na(+) and Mg(2+) in this study) concentrations. Based on the statistical mechanical calculations, we derive a set of empirical formulas for the loop thermodynamic parameters as functions of Na(+) and Mg(2+) concentrations. For three specific types of loops, namely, hairpin, bulge, and internal loops, the predicted free energies agree with the experimental data. Further applications of these empirical formulas to RNA and DNA hairpin stability lead to good agreements with the available experimental data. Our results indicate that the ion-dependent loop stability makes significant contribution to the overall ion-dependence of the hairpin stability.
Figures
FIGURE 1
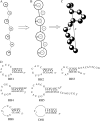
Illustrations of the structural model for single-stranded nucleotide chain used in the work. (A) The virtual-bond model for nucleotide chain (–85). (B) The coarse-grained chain model where P atoms are represented by a series of spheres with charge −e (electronic charge) at the centers (79,89). (C) A three-dimensional chain conformation for the coarse-grained chain model where coordinates of P atoms are produced from the virtual bond model on diamond lattice (–85). (D) The RNA and DNA hairpin sequences used in our calculations. The thermodynamic parameters at 1 M NaCl, and experimental references for these hairpins are listed in Table 2. The values i and j are the numbers of nucleotides of U's and T's in RH6 and DH1 loops, respectively.
FIGURE 2
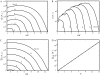
The chain conformational ensemble produced from the virtual bond model on diamond lattice (–85). (A) The number Ω(N, x) of all conformations with end-to-end distance x; (B) the number ω(N, x) of lattice nodes visited by the flexible chain end with end-to-end distance x; (C) the number of chain conformations with x averaged to one direction and (D) the number Ωcoil of chain coil states, which includes all the conformations produced by the self-avoiding walk on a diamond lattice.
FIGURE 3
The calculated loop formation free energy Δ_G_ as functions of end-to-end distance x for different chain-lengths N for the electrostatics-free case (calculated through Eq. 6), i.e., by assuming chain backbone is neutral. The dotted line denotes the DNA hairpin loop free energy at 1 M NaCl for a 13-nt chain (loop size = 11-nt) (36).
FIGURE 4
The partition function z(N, x) averaged for one chain conformation as a function of end-to-end distance x for different Na+ (A_–_C) and Mg2+ (D_–_F) concentrations. The chain lengths are 5-nt (A and D), 9-nt (B and E), and 13-nt (C and F). The averaging is over Ω0 (lines) and Ω0/2 (symbols) randomly selected chain conformations except for the fully stretched conformation. The agreement between lines and symbols show that the calculations are rather stable for different (large) numbers of conformations sampled. The Ω0 values used for calculations are listed in Table 1. For the comparisons, we also show z(N, x) calculated from the PB theory (dotted lines).
FIGURE 5
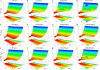
The three-dimensional loop free-energy landscapes Δ_G_/k_B_T as functions of end-to-end distance x for different chain lengths N and different [Na+] (A_–_D) and [Mg2+] (E_–_H). For the comparisons, we also show the loop free energy for different [Mg2+] computed from PB theory (I_–_L). The three-dimensional plots are produced from the empirical formulas for Na+ (Eq. 9), Mg2+ (Eq. 12), and for Mg2+ with the PB treatment (
Data S1
, Eq. S1). The red and blue colors represent the low and high loop free energies, respectively. In
Data S1
, Figs. S11–S13, we shows the comparisons between the calculated results and the respective empirical formulas.
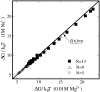
FIGURE 6
The comparisons between the calculated loop free energy Δ_G_ for two typical ionic conditions: 0.01 M MgCl2 and 1 M NaCl. The chain lengths are N = 13, 9, and 5 nucleotides, respectively.
FIGURE 7
The calculated loop free energies Δ_G_ as functions of loop size (N – 2) for different [Na+] and [Mg2+]. (A and D) Hairpin loop; (B and E) bulge loop; and (C and F) internal loop. The symbols are experimental data for RNA (♦) (27) and DNA (□) (36) at 1 M NaCl, and the lines are calculated from Eqs. 15–17, respectively. From the bottom to top, ion concentrations are: (A_–_C) [Na+] = 1 M, 0.1 M, 0.01 M, and 0.001 M; (D_–_F) [Mg2+] = 0.1 M, 0.01 M, 0.001 M, and 0.0001 M, respectively.
FIGURE 8
The RNA hairpin folding free energy Δ_G_°37 (A) and melting temperature _T_m (B) as functions of [Na+] for three sequences RH1, RH2, and RH3. (Symbols) Experimental data: ⋄, RH3 in Na+ solution (20); ▴, RH3 in Na+ solution (95); ♦, RH2 in Na+ solution (49); and □, RH1 in Na+ solution (49). (Solid lines) Predictions with salt-dependent loop free energy (Δ_G_[Na+]); (dotted lines) predictions with invariable loop free energy at 1 M NaCl (Δ_G_[1 M Na+]). Hairpins RH1, RH2, and RH3 are shown in Fig. 1 and Table 2.
FIGURE 9
The RNA hairpin folding free energy Δ_G_°25 (A_–_C) and melting temperature _T_m (D_–_F) as functions of [Mg2+] for different [Na+]. Three sequences used are RH3, RH4, and RH5, which are shown in Fig. 1 and Table 2. (Symbols) Experimental data: (A) ♦, RH3 in 0.054 M [Na+] (20); (E) ♦, RH4 in 0.1 M [K+] (96); (F) ♦, RH5 in 0.1 M [K+] (97). (Solid lines) Predictions with salt (Na+/Mg2+) dependent loop free energy Δ_G_[Na+/Mg2+]; (dotted lines) predictions with invariable loop free energy at 1 M NaCl (Δ_G_[1 M Na+]). In panels A_–_C, we calculate Δ_G_°25 instead of Δ_G_°37 because of the available experimental data at 25°C. In the calculations, we use the same salt empirical formula for K+ as that for Na+, since Na+ and K+ have the similar electrostatic properties (36). For the comparisons, we also show the predictions with the loop free energy from the PB empirical formulas (
Data S1
, Eqs. S1 and S3) (dashed lines).
FIGURE 10
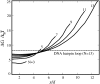
The melting temperatures _T_m of DNA (DH1, A and B) and RNA (RH6, C) hairpins as a function of loop size for different ionic conditions: 0.1 M Na+ (A), 2.5 mM and 33 mM Mg2+ (B), and 2.5 mM Mg2+ (C). (Lines) Predictions from our theory; (symbols) experimental data (93).
Similar articles
- RNA helix stability in mixed Na+/Mg2+ solution.
Tan ZJ, Chen SJ. Tan ZJ, et al. Biophys J. 2007 May 15;92(10):3615-32. doi: 10.1529/biophysj.106.100388. Epub 2007 Feb 26. Biophys J. 2007. PMID: 17325014 Free PMC article. - Sequence dependence of the stability of RNA hairpin molecules with six nucleotide loops.
Vecenie CJ, Morrow CV, Zyra A, Serra MJ. Vecenie CJ, et al. Biochemistry. 2006 Feb 7;45(5):1400-7. doi: 10.1021/bi051750u. Biochemistry. 2006. PMID: 16445282 - Studies of DNA dumbbells. VI. Analysis of optical melting curves of dumbbells with a sixteen-base pair duplex stem and end-loops of variable size and sequence.
Paner TM, Riccelli PV, Owczarzy R, Benight AS. Paner TM, et al. Biopolymers. 1996 Dec;39(6):779-93. doi: 10.1002/(SICI)1097-0282(199612)39:6%3C779::AID-BIP5%3E3.0.CO;2-S. Biopolymers. 1996. PMID: 8946800 - Salt effects on nucleic acids.
Sharp KA, Honig B. Sharp KA, et al. Curr Opin Struct Biol. 1995 Jun;5(3):323-8. doi: 10.1016/0959-440x(95)80093-x. Curr Opin Struct Biol. 1995. PMID: 7583630 Review. - Salt-nucleic acid interactions.
Anderson CF, Record MT Jr. Anderson CF, et al. Annu Rev Phys Chem. 1995;46:657-700. doi: 10.1146/annurev.pc.46.100195.003301. Annu Rev Phys Chem. 1995. PMID: 7495482 Review.
Cited by
- Predicting Monovalent Ion Correlation Effects in Nucleic Acids.
Sun LZ, Zhou Y, Chen SJ. Sun LZ, et al. ACS Omega. 2019 Aug 5;4(8):13435-13446. doi: 10.1021/acsomega.9b01689. eCollection 2019 Aug 20. ACS Omega. 2019. PMID: 31460472 Free PMC article. - MCTBI: a web server for predicting metal ion effects in RNA structures.
Sun LZ, Zhang JX, Chen SJ. Sun LZ, et al. RNA. 2017 Aug;23(8):1155-1165. doi: 10.1261/rna.060947.117. Epub 2017 Apr 27. RNA. 2017. PMID: 28450533 Free PMC article. - Predicting electrostatic forces in RNA folding.
Tan ZJ, Chen SJ. Tan ZJ, et al. Methods Enzymol. 2009;469:465-87. doi: 10.1016/S0076-6879(09)69022-4. Epub 2009 Nov 17. Methods Enzymol. 2009. PMID: 20946803 Free PMC article. - Theory for RNA folding, stretching, and melting including loops and salt.
Einert TR, Netz RR. Einert TR, et al. Biophys J. 2011 Jun 8;100(11):2745-53. doi: 10.1016/j.bpj.2011.04.038. Biophys J. 2011. PMID: 21641320 Free PMC article. - Evaluation of weak interactions of proteins and organic cations with DNA duplex structures.
Morimoto R, Horita M, Yamaguchi D, Nakai H, Nakano SI. Morimoto R, et al. Biophys J. 2022 Aug 2;121(15):2873-2881. doi: 10.1016/j.bpj.2022.07.003. Epub 2022 Jul 5. Biophys J. 2022. PMID: 35791875 Free PMC article.
References
- Bloomfield, V. A., D. M. Crothers, and I. Tinoco, Jr. 2000. Nucleic Acids: Structure, Properties and Functions. University Science Books, Sausalito, CA.
- Tinoco, I., and C. Bustamante. 1999. How RNA folds. J. Mol. Biol. 293:271–281. - PubMed
- Anderson, C. F., and T. M. Record. 1995. Salt-nucleic acid interactions. Annu. Rev. Phys. Chem. 46:657–700. - PubMed
- Bloomfield, V. A. 1997. DNA condensation by multivalent cations. Biopolymers. 44:269–282. - PubMed
- Brion, P., and E. Westhof. 1997. Hierarchy and dynamics of RNA folding. Annu. Rev. Biophys. Biomol. Struct. 26:113–137. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
- R01 GM063732/GM/NIGMS NIH HHS/United States
- R01 GM063732-04/GM/NIGMS NIH HHS/United States
- R01 GM063732-05/GM/NIGMS NIH HHS/United States
- GM063732/GM/NIGMS NIH HHS/United States
LinkOut - more resources
Full Text Sources