Clathrin triskelia show evidence of molecular flexibility - PubMed (original) (raw)
Clathrin triskelia show evidence of molecular flexibility
Matthew L Ferguson et al. Biophys J. 2008 Aug.
Abstract
The clathrin triskelion, which is a three-legged pinwheel-shaped heteropolymer, is a major component in the protein coats of certain post-Golgi and endocytic vesicles. At low pH, or at physiological pH in the presence of assembly proteins, triskelia will self-assemble to form a closed clathrin cage, or "basket". Recent static light scattering and dynamic light scattering studies of triskelia in solution showed that an individual triskelion has an intrinsic pucker similar to, but differing from, that inferred from a high resolution cryoEM structure of a triskelion in a clathrin basket. We extend the earlier solution studies by performing small-angle neutron scattering (SANS) experiments on isolated triskelia, allowing us to examine a higher q range than that probed by static light scattering. Results of the SANS measurements are consistent with the light scattering measurements, but show a shoulder in the scattering function at intermediate q values (0.016 A(-1)), just beyond the Guinier regime. This feature can be accounted for by Brownian dynamics simulations based on flexible bead-spring models of a triskelion, which generate time-averaged scattering functions. Calculated scattering profiles are in good agreement with the experimental SANS profiles when the persistence length of the assumed semiflexible triskelion is close to that previously estimated from the analysis of electron micrographs.
Figures
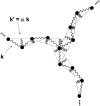
FIGURE 1
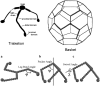
Schematic representations of clathrin triskelia. (Top) Cartoon showing three clathrin heavy-chain legs joined at a common hub, each heavy chain being associated with a clathrin light chain. Also shown is a sketch of a clathrin basket, indicating how the triskelia form a structure having a buckyball-like appearance. (Bottom) Examples of a simple bead model of a clathrin triskelion, defining the leg bend angle, pucker angle, and swivel angle. (a) The leg bend angle, φ, and (b) pucker angle, ψ, were varied from 30° to 180° and 30° to 90°, respectively. (c) The swivel angle, χ, was varied parametrically with the pucker angle according to the equation χ = 3(_ψ_−30)/2, where ψ is measured from the vertical axis shown in panel b.
FIGURE 2
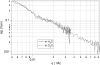
SANS data from clathrin in both H2O (solid) and D2O buffers (dashed). (Error bars and symbols have been removed to illustrate the similarity of both curves.) I(q) is given on an absolute scale in units of cm−1. The clathrin concentration of the D2O sample was 1.5 mg/mL and that of the H2O sample was 2.7 mg/mL. Because the contrasts are different, were the two samples to be at the same concentration, the D2O curve would lie above the H2O curve.
FIGURE 3
I(q) determined by SLS (open circles) and SANS (solid circles) of clathrin triskelia in 0.5 M Tris/D2O, compared with a calculated scattering curve based on a cryoEM structure of clathrin. SANS data are plotted on an absolute scale in units of cm−1; the dashed line shows a scattering function calculated using Eq. 1 for a cryoEM structure of clathrin in a D6 basket (shown in the _upper right_-hand corner), scaled by an empirically determined factor of 0.64 cm−1 so the calculated curve overlaps the SANS data in the range 0.0047 Å−1 < q < 0.0075 Å−1 . (Note the concordance, also, between the data and the calculated curve at high q.) The light scattering data were scaled to fit the (adjusted) calculated curve over the range 0.0006 Å−1 < q < 0.002 Å−1. (The plotted SANS data reflect the fact that a measured background (≈0.1 cm−1), ascribed to the D2O buffer, has been subtracted from SANS data; error bars are related to counting statistics.) The solid lines indicate the power laws _q_−2 (Eq. 3) and _q_−1 (Eq. 4), corresponding to the large q scaling of a flexible Gaussian chain model and a rigid rod, respectively.
FIGURE 4
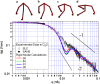
SLS data (open circles) and SANS data (solid circles) of clathrin in 0.5 M Tris/D2O (see caption to Fig. 3), compared with calculated scattering curves for coarse-grained bead models of a rigid triskelion. The solid curves show scattering functions calculated using Eq. 1 for different models (a_–_d, left to right above figure) of a clathrin triskelion, which were made up of 52 beads (see text). These models are in agreement with previous light scattering measurements (SLS and DLS) of clathrin triskelia (4). As done for Fig. 3, the calculated scattering functions (which according to Eq. 1 tends to 1 at q = 0) were scaled by a factor of 0.64 cm−1. Error bars on the data are related to counting statistics.
FIGURE 5
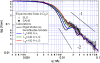
SLS data (open circles) and SANS data (solid circles) of clathrin in 0.5 M Tris/D2O (see captions to Figs. 3 and 4), compared with calculated scattering functions of semiflexible models of a clathrin triskelion characterized by differing values of the persistence length, _L_p. (Values are compared, in the inset, with clathrin leg length, L.) The lines show time-averaged scattering functions calculated from three flexible models of a clathrin triskelion based on the 52-bead model indicated as a at the top of Fig. 4. For comparison, we also show the cross section calculated for the corresponding rigid model. Error bars on the data are related to counting statistics.
FIGURE 6
A schematic of the bead-spring model of a clathrin triskelion used in the Brownian dynamics simulation, showing the common hub and the first four subunits of each leg. Jagged lines represent springs between neighboring subunits, and dotted lines indicate springs between nonneighboring subunits. Torsional motion of the legs is partially prohibited by the addition of a single spring of strength k between each terminal domain (not shown). Some axial rotation is still unconstrained about the axis defined by the triskelion vertex and the end of the leg. Constraining this motion by the insertion of additional springs between the legs did not have a large affect on the time-averaged scattering functions. The figure is based on a scheme introduced in Marques et al. (14).
FIGURE 7
Dependence of the persistence length, _L_p, upon the spring strength, k, as determined from a Brownian dynamics simulation of a bead-spring model performed at room temperature (see Appendix). Symbols show persistence lengths derived from the simulations, and the dotted line shows a square-root fit to the symbols for α = 10. The dark solid line is drawn at the value of _L_p = 350 Å previously determined by from electron micrographs (26).
Similar articles
- Conformation of a clathrin triskelion in solution.
Ferguson ML, Prasad K, Sackett DL, Boukari H, Lafer EM, Nossal R. Ferguson ML, et al. Biochemistry. 2006 May 9;45(18):5916-22. doi: 10.1021/bi052568w. Biochemistry. 2006. PMID: 16669634 Free PMC article. - Folding and trimerization of clathrin subunits at the triskelion hub.
Näthke IS, Heuser J, Lupas A, Stock J, Turck CW, Brodsky FM. Näthke IS, et al. Cell. 1992 Mar 6;68(5):899-910. doi: 10.1016/0092-8674(92)90033-9. Cell. 1992. PMID: 1547490 - Structure and Assembly of Clathrin Cages.
Halebian M, Morris K, Smith C. Halebian M, et al. Subcell Biochem. 2017;83:551-567. doi: 10.1007/978-3-319-46503-6_20. Subcell Biochem. 2017. PMID: 28271490 Review. - Life of a clathrin coat: insights from clathrin and AP structures.
Edeling MA, Smith C, Owen D. Edeling MA, et al. Nat Rev Mol Cell Biol. 2006 Jan;7(1):32-44. doi: 10.1038/nrm1786. Nat Rev Mol Cell Biol. 2006. PMID: 16493411 Review.
Cited by
- Nuclear localization of clathrin involves a labile helix outside the trimerization domain.
Ybe JA, Fontaine SN, Stone T, Nix J, Lin X, Mishra S. Ybe JA, et al. FEBS Lett. 2013 Jan 16;587(2):142-9. doi: 10.1016/j.febslet.2012.11.005. Epub 2012 Nov 21. FEBS Lett. 2013. PMID: 23178717 Free PMC article. - Micellization model for the polymerization of clathrin baskets.
Muthukumar M, Nossal R. Muthukumar M, et al. J Chem Phys. 2013 Sep 28;139(12):121928. doi: 10.1063/1.4816634. J Chem Phys. 2013. PMID: 24089740 Free PMC article. - Systems biology and physical biology of clathrin-mediated endocytosis.
Ramanan V, Agrawal NJ, Liu J, Engles S, Toy R, Radhakrishnan R. Ramanan V, et al. Integr Biol (Camb). 2011 Aug;3(8):803-15. doi: 10.1039/c1ib00036e. Epub 2011 Jul 26. Integr Biol (Camb). 2011. PMID: 21792431 Free PMC article. Review. - Numerical simulation of endocytosis: Viscous flow driven by membranes with non-uniformly distributed curvature-inducing molecules.
Lowengrub J, Allard J, Aland S. Lowengrub J, et al. J Comput Phys. 2016 Mar 15;309:112-128. doi: 10.1016/j.jcp.2015.12.055. J Comput Phys. 2016. PMID: 26869729 Free PMC article. - Interface flexibility controls the nucleation and growth of supramolecular networks.
Caroprese V, Tekin C, Cencen V, Mosayebi M, Asmari N, Liverpool TB, Woolfson DN, Fantner GE, Bastings MMC. Caroprese V, et al. Nat Chem. 2025 Mar;17(3):325-333. doi: 10.1038/s41557-025-01741-y. Epub 2025 Feb 13. Nat Chem. 2025. PMID: 39948282 Free PMC article.
References
- Kirchhausen, T. 2000. Clathrin. Annu. Rev. Biochem. 69:699–727. - PubMed
- Brodsky, F. M., C. Y. Chen, C. Knuehl, M. C. Towler, and D. E. Wakeham. 2001. Biological basket weaving: formation and function of clathrin-coated vesicles. Annu. Rev. Cell Dev. Biol. 17:517–568. - PubMed
- Stagg, S. M., P. LaPointe, and W. E. Balch. 2007. Structural design of cage and coat scaffolds that direct membrane traffic. Curr. Opin. Struct. Biol. 17:221–228. - PubMed
- Fotin, A., Y. F. Cheng, P. Sliz, N. Grigorieff, S. C. Harrison, T. Kirchhausen, and T. Walz. 2004. Molecular model for a complete clathrin lattice from electron cryomicroscopy. Nature. 432:573–579. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources