Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography - PubMed (original) (raw)
Comparative Study
Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography
Gaolang Gong et al. Cereb Cortex. 2009 Mar.
Abstract
The characterization of the topological architecture of complex networks underlying the structural and functional organization of the brain is a basic challenge in neuroscience. However, direct evidence for anatomical connectivity networks in the human brain remains scarce. Here, we utilized diffusion tensor imaging deterministic tractography to construct a macroscale anatomical network capturing the underlying common connectivity pattern of human cerebral cortex in a large sample of subjects (80 young adults) and further quantitatively analyzed its topological properties with graph theoretical approaches. The cerebral cortex was divided into 78 cortical regions, each representing a network node, and 2 cortical regions were considered connected if the probability of fiber connections exceeded a statistical criterion. The topological parameters of the established cortical network (binarized) resemble that of a "small-world" architecture characterized by an exponentially truncated power-law distribution. These characteristics imply high resilience to localized damage. Furthermore, this cortical network was characterized by major hub regions in association cortices that were connected by bridge connections following long-range white matter pathways. Our results are compatible with previous structural and functional brain networks studies and provide insight into the organizational principles of human brain anatomical networks that underlie functional states.
Figures
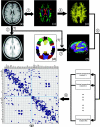
Figure 1.
A flowchart for the construction of the cortical anatomical network in the human brain using DTI tractography. (1) Rigid coregistration from _T_1-weighted structural MRI (a) to DTI native space (c, DTI color-coded map; red: left to right; green: anterior to posterior; blue: inferior to superior) for each subject. (2) Nonlinear registration from the resultant structural MRI to _T_1 template of ICBM152 in the MNI space (b), resulting in a nonlinear transformation (T). (3) Applying the inverse transformation (_T_−1) to the AAL template in the MNI space (d), resulting in the subject-specific AAL mask in the DTI native space (f). All registrations were implemented in the SPM5 package. (4) Reconstructing all the WM fibers (e) in the whole brain by using DTI deterministic tractography. (5) Determining the WM fibers connecting every pair of cortical regions for each subject. (6) Identifying the population-based cortical network matrix (g, blue: 1; blank: 0) by applying nonparametric sign test to every pair of cortical regions (P < 0.05, Bonferroni corrected). For more details, see Materials and Methods. R, right; L, left. The abbreviations of the cortical regions were established by Achard et al. (2006) and are included as the
Supplementary Table 1
.
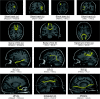
Figure 2.
Examples of cortical connections and their corresponding WM fibers in one subject. The 13 selected cortical connection examples included 4 short WM tracts (a_–_d) and 9 well-known major WM tracts (e_–_g, CC; h, ILF; i, AF; j, SLF; k, UF; l, cingulum; m, IFO) that are well identified with DTI deterministic tractography. As well, the linked cortical regions for each selected connection are listed with the abbreviations in the
Supplementary Table 1
. It should be noted that the fiber bundles shown here are only a part of a specific major WM tract, rather than the entire tract.
Figure 3.
The topological parameters as a function of the statistical threshold. (a) The sparsity of the cortical anatomical networks decreases as the P value threshold lowers (i.e., more conservative statistical criterion). (b) The clustering coefficient ratio (gamma) increases as the P value threshold lowers. (c) The path length ratio (lambda) shows little change as the P value threshold lowers. Overall, the small-worldness of the cortical anatomical network tends to increase as a function of lowering the P value threshold. The cortical anatomical network also exhibits small-world attributes even under very relaxing statistical criterion. The black arrow indicates the values of topological parameter of the human cortical network under our conservative statistical criterion (P < 0.05, Bonferroni corrected, which corresponds to 0.05/(78 × 77/2) = 0.05/3003 ∼1 × 10−5 without correction).
Figure 4.
The topological map of human cortical network. In the map, nodes represent brain cortical regions and lines represent the DTI tractography–derived anatomical connections between regions. Circle size (i.e., diameter) represents the magnitude of normalized node-betweenness centrality (Table 2 and
Supplementary Table 2
). Association, primary, and paralimbic cortex regions are marked as red, blue, and green, respectively. Dark solid lines represent bridge connections with high normalized edge-betweenness values (Table 3). The geometric distance between regions on the drawing space approximately corresponds to the shortest path length between them. The network was visualized with the Pajek software with slight manual adjustment for the locations of brain regions (Batagelj and Mrvar 1998). For the abbreviations of the regions, see
Supplementary Table 1
.
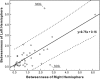
Figure 5.
The relation between the node betweenness of left and right hemispheres. Each circle represents one cortical region (39 in total). The black line indicates the linear-fitted curve and the dash lines indicate 95% confidence interval. The node betweenness of left hemisphere is linearly correlated with that of right hemisphere (t = 6.2, P < 10−6). Of note, the absolute betweenness centrality of some individual cortical regions (e.g., MOG and SOG) demonstrates large hemispheric asymmetry.
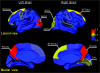
Figure 6.
Node betweenness centrality map on the human cerebral cortex. According to the AAL template (Tzourio-Mazoyer et al. 2002), the cerebral cortex was parcellated into 78 regions (39 per hemisphere), each representing a node in the anatomical cortical network. Regions were mapped into an average cortical surface obtained from ICBM152 according to their normalized betweenness centrality values. The color bar indicating the range of normalized node betweenness is shown on the right. Hub regions identified in this study are marked on the map. Note that several hubs (PCUN, SFGdor, and MOG) appear in a bilaterally symmetric fashion (for details, see Table 2).
Figure 7.
The degree and betweenness distributions of the human cortical network. (a) Log-log plot of the cumulative node degree distribution; (b) log-log plot of the cumulative node-betweenness distribution; (c) log-log plot of the cumulative edge-betweenness distribution. The plus sign represents observed data, the solid line is the fit of the exponentially truncated power-law (p(x) ∼ _x_α−1exp(x/xc)), the dashed line is an exponential (p(x) ∼ exp(x/xc)), and the dotted line is a power-law (p(x) ∼ _x_α−1). _R_2 was calculated to assess the goodness-of-fit (a larger value indicates a better fitting; _R_etp, _R_2 for exponentially truncated power-law fit; Re, _R_2 for exponential fit; Rp, _R_2 for power-law fit). The exponentially truncated power-law is the best fitting for all the 3 distributions (a, estimated exponent α = 1.66 and cutoff degree _kc_node = 3.65; b, estimated exponent α = 0.96 and cutoff betweenness _B_cnode = 76.93; c, estimated exponent α = 1.10 and cutoff betweenness _B_cedge = 18.95).
Similar articles
- Sex- and brain size-related small-world structural cortical networks in young adults: a DTI tractography study.
Yan C, Gong G, Wang J, Wang D, Liu D, Zhu C, Chen ZJ, Evans A, Zang Y, He Y. Yan C, et al. Cereb Cortex. 2011 Feb;21(2):449-58. doi: 10.1093/cercor/bhq111. Epub 2010 Jun 18. Cereb Cortex. 2011. PMID: 20562318 - Small-world anatomical networks in the human brain revealed by cortical thickness from MRI.
He Y, Chen ZJ, Evans AC. He Y, et al. Cereb Cortex. 2007 Oct;17(10):2407-19. doi: 10.1093/cercor/bhl149. Epub 2007 Jan 4. Cereb Cortex. 2007. PMID: 17204824 - Age- and gender-related differences in the cortical anatomical network.
Gong G, Rosa-Neto P, Carbonell F, Chen ZJ, He Y, Evans AC. Gong G, et al. J Neurosci. 2009 Dec 16;29(50):15684-93. doi: 10.1523/JNEUROSCI.2308-09.2009. J Neurosci. 2009. PMID: 20016083 Free PMC article. - The structural and functional connectivity of the posterior cingulate cortex: comparison between deterministic and probabilistic tractography for the investigation of structure-function relationships.
Khalsa S, Mayhew SD, Chechlacz M, Bagary M, Bagshaw AP. Khalsa S, et al. Neuroimage. 2014 Nov 15;102 Pt 1:118-27. doi: 10.1016/j.neuroimage.2013.12.022. Epub 2013 Dec 21. Neuroimage. 2014. PMID: 24365673 Review. - Graph theoretical analysis of human brain structural networks.
Lo CY, He Y, Lin CP. Lo CY, et al. Rev Neurosci. 2011;22(5):551-63. doi: 10.1515/RNS.2011.039. Epub 2011 Aug 24. Rev Neurosci. 2011. PMID: 21861783 Review.
Cited by
- Group-wise consistent cortical parcellation based on connectional profiles.
Zhang T, Zhu D, Jiang X, Zhang S, Kou Z, Guo L, Liu T. Zhang T, et al. Med Image Anal. 2016 Aug;32:32-45. doi: 10.1016/j.media.2016.02.009. Epub 2016 Mar 14. Med Image Anal. 2016. PMID: 27054276 Free PMC article. - An integrated framework for high angular resolution diffusion imaging-based investigation of structural connectivity.
Bloy L, Ingalhalikar M, Batmanghelich NK, Schultz RT, Roberts TP, Verma R. Bloy L, et al. Brain Connect. 2012;2(2):69-79. doi: 10.1089/brain.2011.0070. Epub 2012 Jun 11. Brain Connect. 2012. PMID: 22500705 Free PMC article. - Longitudinal development of the human white matter structural connectome and its association with brain transcriptomic and cellular architecture.
Feng G, Chen R, Zhao R, Li Y, Ma L, Wang Y, Men W, Gao J, Tan S, Cheng J, He Y, Qin S, Dong Q, Tao S, Shu N. Feng G, et al. Commun Biol. 2023 Dec 12;6(1):1257. doi: 10.1038/s42003-023-05647-8. Commun Biol. 2023. PMID: 38087047 Free PMC article. - Test-retest reliability of computational network measurements derived from the structural connectome of the human brain.
Owen JP, Ziv E, Bukshpun P, Pojman N, Wakahiro M, Berman JI, Roberts TP, Friedman EJ, Sherr EH, Mukherjee P. Owen JP, et al. Brain Connect. 2013;3(2):160-76. doi: 10.1089/brain.2012.0121. Brain Connect. 2013. PMID: 23350832 Free PMC article. - Cognitive Flexibility through Metastable Neural Dynamics Is Disrupted by Damage to the Structural Connectome.
Hellyer PJ, Scott G, Shanahan M, Sharp DJ, Leech R. Hellyer PJ, et al. J Neurosci. 2015 Jun 17;35(24):9050-63. doi: 10.1523/JNEUROSCI.4648-14.2015. J Neurosci. 2015. PMID: 26085630 Free PMC article.
References
- Albert R, Jeong H, Barabasi AL. Error and attack tolerance of complex networks. Nature. 2000;406:378–382. - PubMed
- Amunts K, Schleicher A, Burgel U, Mohlberg H, Uylings HB, Zilles K. Broca's region revisited: cytoarchitecture and intersubject variability. J Comp Neurol. 1999;412:319–341. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources