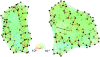Systematic multiscale parameterization of heterogeneous elastic network models of proteins - PubMed (original) (raw)
Systematic multiscale parameterization of heterogeneous elastic network models of proteins
Edward Lyman et al. Biophys J. 2008.
Abstract
We present a method to parameterize heterogeneous elastic network models (heteroENMs) of proteins to reproduce the fluctuations observed in atomistic simulations. Because it is based on atomistic simulation, our method allows the development of elastic coarse-grained models of proteins under different conditions or in different environments. The method is simple and applicable to models at any level of coarse-graining. We validated the method in three systems. First, we computed the persistence length of ADP-bound F-actin, using a heteroENM model. The value of 6.1 +/- 1.6 microm is consistent with the experimentally measured value of 9.0 +/- 0.5 microm. We then compared our method to a uniform elastic network model and a realistic extension algorithm via covariance Hessian (REACH) model of carboxy myoglobin, and found that the heteroENM method more accurately predicted mean-square fluctuations of alpha-carbon atoms. Finally, we showed that the method captures critical differences in effective harmonic interactions for coarse-grained models of the N-terminal Bin/amphiphysin/Rvs (N-BAR) domain of amphiphysin, by building models of N-BAR both bound to a membrane and free in solution.
Figures
FIGURE 1
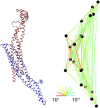
Two views of an α_-carbon heteroENM model of myoglobin. Pairs of C_α atoms separated on average by <15 Å are connected by a harmonic spring, indicated by colored lines. Stiffness of the spring is represented by its color on a logarithmic scale, from ∼100 kcal mol−1Å−2 (red) to 0.01 kcal mol−1Å−2 (blue). The N-terminus is indicated by a red ball (at left), and the plane of the heme is indicated by a black line (right). The image was rendered with Kinemage, next generation (54).
FIGURE 2
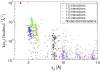
Spring constant as a function of equilibrium length _x_0 for the myoglobin heteroENM model in Fig. 1. Points are colored to indicate whether they are between neighboring _α_-carbons (1–2 interactions), next-neighbor _α_-carbons (1–3 interactions), etc. Interactions cluster into distinct groups, even as far out as 1–6 related _α_-carbons.
FIGURE 3
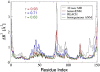
Per-residue mean-square fluctuations computed from atomistic MD simulation, heteroENM, REACH, and single-parameter ENM. Neither the heteroENM nor REACH models were parameterized to reproduce these data. Agreement between the MD simulation and ENM models, as measured by linear correlation coefficient r, is best for the heteroENM model.
FIGURE 4
Side view of bound N-BAR domain model, comparing backbone level structure (left) with heteroENM model (right). The CG-site definitions are symmetric across the homodimer. Residues corresponding to CG sites are 26–31, 32–55, 56–103, 104–132, 133–150, 151–163, 164–173, 174–192, 193–218, and 219–244. Ribbon diagram was rendered using visual molecular dynamics (55), and network diagram was rendered using Kinemage, next generation (54).
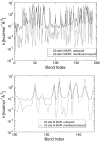
FIGURE 5
(Top) Comparison of spring constants determined by a heteroENM calculation between membrane-bound and unbound N-BAR domains. The horizontal axis labels the CG harmonic bonds; the vertical axis is logarithmic to emphasize the difference between the two cases. (Bottom) Close-up of A for bonds numbered 100–150. To test whether observed differences were significant, error bars were calculated by performing the heteroENM calculation separately for five adjacent 2-ns blocks of atomistic simulations, and computing the standard deviation of resultant spring constants. Error bars are typically on the order of 1–5%. Many of the spring constants differ by far more than the range of their error bars. Moreover, error bars address the convergence of the heteroENM model by demonstrating that k values computed from 2-ns blocks agree with those computed from the full 10-ns trajectory.
Similar articles
- Coarse-grained biomolecular simulation with REACH: realistic extension algorithm via covariance Hessian.
Moritsugu K, Smith JC. Moritsugu K, et al. Biophys J. 2007 Nov 15;93(10):3460-9. doi: 10.1529/biophysj.107.111898. Epub 2007 Aug 10. Biophys J. 2007. PMID: 17693469 Free PMC article. - REACH coarse-grained biomolecular simulation: transferability between different protein structural classes.
Moritsugu K, Smith JC. Moritsugu K, et al. Biophys J. 2008 Aug;95(4):1639-48. doi: 10.1529/biophysj.108.131714. Epub 2008 May 9. Biophys J. 2008. PMID: 18469078 Free PMC article. - Defining coarse-grained representations of large biomolecules and biomolecular complexes from elastic network models.
Zhang Z, Pfaendtner J, Grafmüller A, Voth GA. Zhang Z, et al. Biophys J. 2009 Oct 21;97(8):2327-37. doi: 10.1016/j.bpj.2009.08.007. Biophys J. 2009. PMID: 19843465 Free PMC article. - Fluctuation matching approach for elastic network model and structure-based model of biomacromolecules.
Bope CD, Tong D, Li X, Lu L. Bope CD, et al. Prog Biophys Mol Biol. 2017 Sep;128:100-112. doi: 10.1016/j.pbiomolbio.2016.12.006. Epub 2016 Dec 30. Prog Biophys Mol Biol. 2017. PMID: 28043838 Review. - Coarse-Grained Protein Dynamics Studies Using Elastic Network Models.
Togashi Y, Flechsig H. Togashi Y, et al. Int J Mol Sci. 2018 Dec 5;19(12):3899. doi: 10.3390/ijms19123899. Int J Mol Sci. 2018. PMID: 30563146 Free PMC article. Review.
Cited by
- Multi-scale characterization of the energy landscape of proteins with application to the C3D/Efb-C complex.
Haspel N, Geisbrecht BV, Lambris J, Kavraki L. Haspel N, et al. Proteins. 2010 Mar;78(4):1004-14. doi: 10.1002/prot.22624. Proteins. 2010. PMID: 19899169 Free PMC article. - Structure-Encoded Global Motions and Their Role in Mediating Protein-Substrate Interactions.
Bahar I, Cheng MH, Lee JY, Kaya C, Zhang S. Bahar I, et al. Biophys J. 2015 Sep 15;109(6):1101-9. doi: 10.1016/j.bpj.2015.06.004. Epub 2015 Jul 2. Biophys J. 2015. PMID: 26143655 Free PMC article. Review. - Hierarchical coarse-graining strategy for protein-membrane systems to access mesoscopic scales.
Ayton GS, Lyman E, Voth GA. Ayton GS, et al. Faraday Discuss. 2010;144:347-57; discussion 445-81. doi: 10.1039/b901996k. Faraday Discuss. 2010. PMID: 20158037 Free PMC article. - Effects of ATP and actin-filament binding on the dynamics of the myosin II S1 domain.
Baker JL, Voth GA. Baker JL, et al. Biophys J. 2013 Oct 1;105(7):1624-34. doi: 10.1016/j.bpj.2013.08.023. Biophys J. 2013. PMID: 24094403 Free PMC article. - Coarse-Graining with Equivariant Neural Networks: A Path Toward Accurate and Data-Efficient Models.
Loose TD, Sahrmann PG, Qu TS, Voth GA. Loose TD, et al. J Phys Chem B. 2023 Dec 14;127(49):10564-10572. doi: 10.1021/acs.jpcb.3c05928. Epub 2023 Nov 30. J Phys Chem B. 2023. PMID: 38033234 Free PMC article.
References
- Tozzini, V. 2005. Coarse-grained models for proteins. Curr. Opin. Struct. Biol. 15:144–150. - PubMed
- Ayton, G. S., W. G. Noid, and G. A. Voth. 2007. Multiscale modeling of biomolecular systems in serial and in parallel. Curr. Opin. Struct. Biol. 17:192–198. - PubMed
- Ma, J. 2005. Usefulness and limitations of normal mode analysis in modeling dynamics of biomolecular complexes. Structure. 13:373–380. - PubMed
- Rader, A. J., C. Chennubhotla, L.-W. Yang, and I. Bahar. 2006. The gaussian network model: theory and applications. In Normal Mode Analysis. Theory and Applications to Biological and Chemical Systems. Q. Cui, and I. Bahar, editors. New York, Taylor and Francis Group. 41–64.
- Halioglu, T., I. Bahar, and B. Erman. 1997. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 79:3090–3094.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources