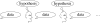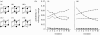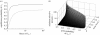Review. Theoretical and empirical evidence for the impact of inductive biases on cultural evolution - PubMed (original) (raw)
Review
Review. Theoretical and empirical evidence for the impact of inductive biases on cultural evolution
Thomas L Griffiths et al. Philos Trans R Soc Lond B Biol Sci. 2008.
Abstract
The question of how much the outcomes of cultural evolution are shaped by the cognitive capacities of human learners has been explored in several disciplines, including psychology, anthropology and linguistics. We address this question through a detailed investigation of transmission chains, in which each person passes information to another along a chain. We review mathematical and empirical evidence that shows that under general conditions, and across experimental paradigms, the information passed along transmission chains will be affected by the inductive biases of the people involved-the constraints on learning and memory, which influence conclusions from limited data. The mathematical analysis considers the case where each person is a rational Bayesian agent. The empirical work consists of behavioural experiments in which human participants are shown to operate in the manner predicted by the Bayesian framework. Specifically, in situations in which each person's response is used to determine the data seen by the next person, people converge on concepts consistent with their inductive biases irrespective of the information seen by the first member of the chain. We then relate the Bayesian analysis of transmission chains to models of biological evolution, clarifying how chains of individuals correspond to population-level models and how selective forces can be incorporated into our models. Taken together, these results indicate how laboratory studies of transmission chains can provide information about the dynamics of cultural evolution and illustrate that inductive biases can have a significant impact on these dynamics.
Figures
Figure 1
Transmission chains provide a simple setting for studying cultural transmission that has been used in psychology, anthropology and linguistics. In a transmission chain, each agent observes the data generated by the previous agent, forms a hypothesis about the source of these data and then uses that hypothesis to generate data for the next agent.
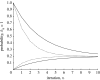
Figure 2
Dynamics of the probability of an agent adopting hypothesis 1 as a function of the number of generations of transmission. As the number of generations increases, the probability of choosing _h_1 converges to the prior probability, _π_=0.2. The noise parameter ϵ determines the rate of convergence, with _ϵ_=0.01 (solid lines) converging more slowly than _ϵ_=0.05 (dotted lines).
Figure 3
Transmission chains for categories. (a) If we consider categories that are sets of four objects defined on three binary dimensions and ignore the assignment of the dimensions to the physical properties of those objects, there are just six possible category types (i–vi), types I–VI (Shepard et al. 1961). Each of the six types is illustrated on a cube, where each dimension of the cube corresponds to one of the binary dimensions and the vertices are the eight objects. Filled circles represent members of an example category of that type. Type I categories are defined on one dimension; type II uses two dimensions; types III, IV and V are one dimension plus an exception and type VI uses all three dimensions. (b) Transmission chains were constructed by showing people three objects drawn from a category and asking them to indicate, from a set of possible alternatives, which object completed the set. The objects seen by the next person were selected at random from the set selected by the previous person. The probability with which people selected categories of the six types changes as a function of the number of generations of a transmission chain, as predicted by a Bayesian model using a prior estimated from human learning data. In particular, the probabilities of types I and VI increase and decrease, respectively. (i) Human participants and (ii) Bayesian model (circles, type I; crosses, type II; triangles, type III; squares, type IV; five-point stars, type V; six-point stars, type VI). Further details are provided in Griffiths et al. (2008).
Figure 4
Representative results for transmission chains with human participants in which people learn functions. (a–d) Each row shows a single chain. (i) The (x, y) pairs were presented to the first participant in the chain, being represented as the width and height of horizontal and vertical rectangles, respectively. Participants then made predictions of the value of y for new x values ((ii) _n_=1, (iii) _n_=2, (iv) _n_=3, (v) _n_=4, (vi) _n_=5, (vii) _n_=6, (viii) _n_=7, (ix) _n_=8, (x) _n_=9). These predictions formed the (x, y) pairs given to the next person in the chain, whose data appear in (ii)–(x) and so forth. Consistent with the previous research exploring human inductive biases for function learning, chains produced linear functions with mostly positive slopes, regardless of whether they were initialized with (a) a positive linear function, (b) a negative linear function, (c) a nonlinear function or (d) a random collection of points.
Figure 5
The interaction of selection with inductive biases. (a) Increasing the selective pressure in favour of hypothesis 1 increases the representation of that hypothesis in the population. The equilibrium probability of hypothesis 1 for _π_=0.2, _ϵ_∈{0.01,0.05} (solid line, dotted line, respectively), and a range of values of the selective pressure s are shown. (b) Threshold on s for hypothesis 1 to obtain an equilibrium probability greater than 0.5 as a function of π and ϵ. For values of π and ϵ such that _q_21>0.5, no value of s produces an equilibrium favouring hypothesis 1.
Similar articles
- A rational analysis of the effects of memory biases on serial reproduction.
Xu J, Griffiths TL. Xu J, et al. Cogn Psychol. 2010 Mar;60(2):107-26. doi: 10.1016/j.cogpsych.2009.09.002. Epub 2009 Oct 30. Cogn Psychol. 2010. PMID: 19879560 - When Extremists Win: Cultural Transmission Via Iterated Learning When Populations Are Heterogeneous.
Navarro DJ, Perfors A, Kary A, Brown SD, Donkin C. Navarro DJ, et al. Cogn Sci. 2018 Sep;42(7):2108-2149. doi: 10.1111/cogs.12667. Epub 2018 Jul 31. Cogn Sci. 2018. PMID: 30062733 - The evolution of frequency distributions: relating regularization to inductive biases through iterated learning.
Reali F, Griffiths TL. Reali F, et al. Cognition. 2009 Jun;111(3):317-28. doi: 10.1016/j.cognition.2009.02.012. Epub 2009 Mar 26. Cognition. 2009. PMID: 19327759 - Review. The multiple roles of cultural transmission experiments in understanding human cultural evolution.
Mesoudi A, Whiten A. Mesoudi A, et al. Philos Trans R Soc Lond B Biol Sci. 2008 Nov 12;363(1509):3489-501. doi: 10.1098/rstb.2008.0129. Philos Trans R Soc Lond B Biol Sci. 2008. PMID: 18801720 Free PMC article. Review. - Learning bias, cultural evolution of language, and the biological evolution of the language faculty.
Smith K. Smith K. Hum Biol. 2011 Apr;83(2):261-78. doi: 10.3378/027.083.0207. Hum Biol. 2011. PMID: 21615289 Review.
Cited by
- The origins of duality of patterning in artificial whistled languages.
Verhoef T. Verhoef T. Lang Cogn. 2012 Nov 1;4(4):357-380. doi: 10.1515/langcog-2012-0019. Lang Cogn. 2012. PMID: 23637710 Free PMC article. - Brain potentials predict learning, transmission and modification of an artificial symbolic system.
Lumaca M, Baggio G. Lumaca M, et al. Soc Cogn Affect Neurosci. 2016 Dec;11(12):1970-1979. doi: 10.1093/scan/nsw112. Epub 2016 Aug 10. Soc Cogn Affect Neurosci. 2016. PMID: 27510496 Free PMC article. - Hybrid social learning in human-algorithm cultural transmission.
Brinkmann L, Gezerli D, Kleist KV, Müller TF, Rahwan I, Pescetelli N. Brinkmann L, et al. Philos Trans A Math Phys Eng Sci. 2022 Jul 11;380(2227):20200426. doi: 10.1098/rsta.2020.0426. Epub 2022 May 23. Philos Trans A Math Phys Eng Sci. 2022. PMID: 35599570 Free PMC article. - Cultural selection and biased transformation: two dynamics of cultural evolution.
Mesoudi A. Mesoudi A. Philos Trans R Soc Lond B Biol Sci. 2021 Jul 5;376(1828):20200053. doi: 10.1098/rstb.2020.0053. Epub 2021 May 17. Philos Trans R Soc Lond B Biol Sci. 2021. PMID: 33993764 Free PMC article. Review. - Counterintuitive Pseudoscience Propagates by Exploiting the Mind's Communication Evaluation Mechanisms.
Mermelstein S, German TC. Mermelstein S, et al. Front Psychol. 2021 Oct 5;12:739070. doi: 10.3389/fpsyg.2021.739070. eCollection 2021. Front Psychol. 2021. PMID: 34675845 Free PMC article.
References
- Anderson J.R. Erlbaum; Hillsdale, NJ: 1990. The adaptive character of thought.
- Anderson J.R. The adaptive nature of human categorization. Psychol. Rev. 1991;98:409–429. doi:10.1037/0033-295X.98.3.409 - DOI
- Anderson J.R, Milson R. Human memory: an adaptive perspective. Psychol. Rev. 1989;96:703–719. doi:10.1037/0033-295X.96.4.703 - DOI
- Ashby F.G, Alfonso-Reese L.A. Categorization as probability density estimation. J. Math. Psychol. 1995;39:216–233. doi:10.1006/jmps.1995.1021 - DOI
- Atran S. The trouble with memes: inferences versus imitation in cultural creation. Hum. Nat. 2001;12:351–381. doi:10.1007/s12110-001-1003-0 - DOI - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources