A minimalist network model for coarse-grained normal mode analysis and its application to biomolecular x-ray crystallography - PubMed (original) (raw)

A minimalist network model for coarse-grained normal mode analysis and its application to biomolecular x-ray crystallography

Mingyang Lu et al. Proc Natl Acad Sci U S A. 2008.

Abstract

In this article, we report a method for coarse-grained normal mode analysis called the minimalist network model. The main features of the method are that it can deliver accurate low-frequency modes on structures without undergoing initial energy minimization and that it also retains the details of molecular interactions. The method does not require any additional adjustable parameters after coarse graining and is computationally very fast. Tests on modeling the experimentally measured anisotropic displacement parameters in biomolecular x-ray crystallography demonstrate that the method can consistently perform better than other commonly used methods including our own one. We expect this method to be effective for applications such as structural refinement and conformational sampling.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Fig. 1.

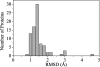
Fig. 1.

The distribution of heavy-atom RMSD between protein structures before and after initial energy minimization. The histogram was generated from 83 ultra-high-resolution protein crystal structures, which have at least 50 residues, are at least 1 Å in resolution, and share <50% sequence identity. For more details on the protein test set and minimization protocol, see Methods.

Fig. 2.

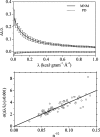
Fig. 2.

Relative differences of eigenvalues. (Upper) Average relative difference of eigenvalues as a function of RTB eigenvalues for PD (dashed line) and the MNM (solid line). The statistics were derived from the first 1,000 modes with eigenvalues of <1.0 kcal·g−1·Å−2 on all 83 ultra-high-resolution protein structures. The SDs are shown as vertical lines. (Lower) SDs for relative differences of eigenvalues (circles) as a function of inverse square root of the number of residues (n). For each of the 83 test proteins, the SD was calculated for the first 1,000 normal modes with eigenvalues ranging from 0.2 to 0.8 kcal·g−1·Å−2 (as a representative range). The linear correlation coefficient is 0.97, and the slope is ≈0.04.

Fig. 3.

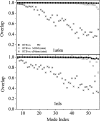
Fig. 3.

Overlap of the lowest-frequency mode subspaces between various normal mode analyses. Tests were performed on two proteins: PDB ID codes 1a6m (Upper) and 1nls (Lower). The methods RTB, PD, MNM, and elNémo were applied to the structures after energy minimization, and overlap was calculated by projecting the modes of each method onto the 50-lowest-frequency-normal-mode subspace of RTB.

Fig. 4.

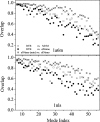
Fig. 4.

Overlap of the lowest-frequency mode subspaces between various normal mode analyses. Tests were performed on two proteins: PDB ID codes 1a6m (Upper) and 1nls (Lower). The MNM was applied to relaxed structures, RTB to native structure, and elNémo to both native and minimized structures. For all comparisons, overlap was calculated by projecting the modes of each method onto the 50-lowest-frequency-normal-mode subspace of RTB, with the exception of the overlap between the two elNémo methods (stars), for which the modes were projected onto the 50-lowest-frequency-normal-mode subspace of elNémo on minimized structures.

Fig. 5.

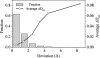
Fig. 5.

Average KL distance improvement from RTB (on minimized structures) to the MNM (on unminimized structures) as a function of atomic positional deviation after energy minimization. The changes in KL distance from RTB to the MNM (Δ_D_KL = DKLRTB − DKLMNM) were calculated and averaged over atoms with similar positional deviations. This figure presents both the histogram of deviations (y axis to the left) and the average improvements in KL distance (y axis to the right). The average KL distance from RTB to the MNM improves for all deviation ranges (i.e., Δ_D_KL > 0), and the improvements tend to be larger for larger structure deviations.

Similar articles

Cited by

References

    1. Brooks B, Karplus M. Harmonic dynamics of proteins: Normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc Natl Acad Sci USA. 1983;80:6571–6575. - PMC - PubMed
    1. Go N, Noguti T, Nishikawa T. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc Natl Acad Sci USA. 1983;80:3696–3700. - PMC - PubMed
    1. Levitt M, Sander C, Stern PS. Protein normal-mode dynamics: Trypsin inhibitor, crambin, ribonuclease and lysozyme. J Mol Biol. 1985;181:423–447. - PubMed
    1. Brooks BR, Janezic D, Karplus M. Harmonic analysis of large systems. I. Methodology. J Comput Chem. 1995;16:1522–1542.
    1. Ma J. Usefulness and limitations of normal mode analysis in modeling dynamics of biomolecular complexes. Structure (London) 2005;13:373–380. - PubMed

Publication types

MeSH terms

Substances

LinkOut - more resources