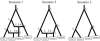Inferring population history with DIY ABC: a user-friendly approach to approximate Bayesian computation - PubMed (original) (raw)
Inferring population history with DIY ABC: a user-friendly approach to approximate Bayesian computation
Jean-Marie Cornuet et al. Bioinformatics. 2008.
Abstract
Genetic data obtained on population samples convey information about their evolutionary history. Inference methods can extract part of this information but they require sophisticated statistical techniques that have been made available to the biologist community (through computer programs) only for simple and standard situations typically involving a small number of samples. We propose here a computer program (DIY ABC) for inference based on approximate Bayesian computation (ABC), in which scenarios can be customized by the user to fit many complex situations involving any number of populations and samples. Such scenarios involve any combination of population divergences, admixtures and population size changes. DIY ABC can be used to compare competing scenarios, estimate parameters for one or more scenarios and compute bias and precision measures for a given scenario and known values of parameters (the current version applies to unlinked microsatellite data). This article describes key methods used in the program and provides its main features. The analysis of one simulated and one real dataset, both with complex evolutionary scenarios, illustrates the main possibilities of DIY ABC.
Availability: The software DIY ABC is freely available at http://www.montpellier.inra.fr/CBGP/diyabc.
Figures
Fig. 1.
First example: the three evolutionary scenarios. The dataset used as an example has been simulated according to scenario 1 (left). The parameter values were the following: all populations had an effective (diploid) size of 1000, the times of successive events (backward in time) were _t_1 = 10, _t_2 = 500, _t_3 = 10 000, _t_4 = 20 000 and _t_5 = 200 000, the two admixture rates were _r_1 = 0.6 and _r_2 = 0.4. Scenario 1 includes six populations, the four that have been sampled and two left parental populations in the admixture events. Scenario 2 and 3 include 5 and 4 populations, respectively. Samples 3 and 4 have been collected 2 and 4 generations earlier than the first two samples, hence their slightly upward locations on the graphs. Time is not at scale.
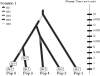
Fig. 2.
Second example: screenshot of the scenario used in the analysis of the Z. lateralis lateralis dataset. In 1830, Z. l. lateralis colonized the South Island of New Zealand (Pop 2) from Tasmania (Pop 1). In the following years, the population began expanding and dispersing, and reached the North Island by 1856 (Pop 3). Chatham Island (Pop 4) was colonized in 1856 from the South Island, and Norfolk Island (Pop 5) was colonized in 1904 from the North Island (historical information reviewed in Estoup and Clegg 2003). Sample collection times are 1997 for Tasmania (Sa 1), South and North Island of New Zealand (Sa 2 and Sa 3, respectively), Chatham Island (Sa 4) and Norfolk Island (Sa 5), 1994 for the second sample from Norfolk (Sa 6), and 1992 for the second sample from the North Island of New Zealand (Sa 7). Splitting events and sampling dates in years were translated in number of generations since the most recent sampling date by assuming a generation time of 3 years (Estoup and Clegg, 2003). We hence fixed t1, t2, t3 and t4 to 31, 47, 47 and 56 generations, respectively.
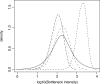
Fig. 3.
Second example: posterior distributions of the bottleneck severity (see definition in text) for the invasions of four Pacific Islands by Z.lateralis lateralis. The four discontinuous lines with small dashes, dots, dash-dots and long dashes correspond to Norfolk, Chatham, North Island and South Island of New Zealand, respectively. The continuous line corresponds to the prior distribution, which is identical for each island. This graph has been made with the locfit function of the R statistical package (Ihaka and Gentleman, 1996), using an option of DIYABC which saves the sample of the parameter values adjusted by the local linear regression (Beaumont et al., 2002).
Similar articles
- Inference on population history and model checking using DNA sequence and microsatellite data with the software DIYABC (v1.0).
Cornuet JM, Ravigné V, Estoup A. Cornuet JM, et al. BMC Bioinformatics. 2010 Jul 28;11:401. doi: 10.1186/1471-2105-11-401. BMC Bioinformatics. 2010. PMID: 20667077 Free PMC article. - DIYABC v2.0: a software to make approximate Bayesian computation inferences about population history using single nucleotide polymorphism, DNA sequence and microsatellite data.
Cornuet JM, Pudlo P, Veyssier J, Dehne-Garcia A, Gautier M, Leblois R, Marin JM, Estoup A. Cornuet JM, et al. Bioinformatics. 2014 Apr 15;30(8):1187-1189. doi: 10.1093/bioinformatics/btt763. Epub 2014 Jan 2. Bioinformatics. 2014. PMID: 24389659 - Inferring introduction routes of invasive species using approximate Bayesian computation on microsatellite data.
Guillemaud T, Beaumont MA, Ciosi M, Cornuet JM, Estoup A. Guillemaud T, et al. Heredity (Edinb). 2010 Jan;104(1):88-99. doi: 10.1038/hdy.2009.92. Heredity (Edinb). 2010. PMID: 19654609 - On the use of kernel approximate Bayesian computation to infer population history.
Nakagome S. Nakagome S. Genes Genet Syst. 2015;90(3):153-62. doi: 10.1266/ggs.90.153. Genes Genet Syst. 2015. PMID: 26510570 Review. - ABC as a flexible framework to estimate demography over space and time: some cons, many pros.
Bertorelle G, Benazzo A, Mona S. Bertorelle G, et al. Mol Ecol. 2010 Jul;19(13):2609-25. doi: 10.1111/j.1365-294X.2010.04690.x. Epub 2010 Jun 18. Mol Ecol. 2010. PMID: 20561199 Review.
Cited by
- Genetic structure of populations of Salvia ceratophylloides endemic to southern Calabria (southern Italy).
Laface VLA, Cavallini M, Di Iorio A, Lombardo G, Binelli G, Sorgonà A, Musarella CM, Spampinato G. Laface VLA, et al. Heliyon. 2024 Aug 8;10(16):e35875. doi: 10.1016/j.heliyon.2024.e35875. eCollection 2024 Aug 30. Heliyon. 2024. PMID: 39247277 Free PMC article. - A Comparative Genetic Analysis of Phoenix atlantica in Cape Verde.
Sarmiento Cabello S, Rodríguez-Rodríguez P, Arbelo Ramírez G, Naranjo-Cigala A, Curbelo L, da Graca Gomes MM, Brito J, Aberlenc F, Zehdi-Azouzi S, Sosa PA. Sarmiento Cabello S, et al. Plants (Basel). 2024 Aug 9;13(16):2209. doi: 10.3390/plants13162209. Plants (Basel). 2024. PMID: 39204645 Free PMC article. - Across two phylogeographic breaks: Quaternary evolutionary history of a mountain aspen (Populus rotundifolia) in the Hengduan Mountains.
Tang J, Fan X, Milne RI, Yang H, Tao W, Zhang X, Guo M, Li J, Mao K. Tang J, et al. Plant Divers. 2024 Apr 3;46(3):321-332. doi: 10.1016/j.pld.2024.03.009. eCollection 2024 May. Plant Divers. 2024. PMID: 38798733 Free PMC article. - Historical fragmentation and stepping-stone gene flow led to population genetic differentiation in a coastal seabird.
Harkness BAS, Ibarguchi G, Poland VF, Friesen VL. Harkness BAS, et al. Ecol Evol. 2024 Apr 17;14(4):e11204. doi: 10.1002/ece3.11204. eCollection 2024 Apr. Ecol Evol. 2024. PMID: 38633521 Free PMC article. - Nuclear genetic diversity of head lice sheds light on human dispersal around the world.
Ascunce MS, Toloza AC, González-Oliver A, Reed DL. Ascunce MS, et al. PLoS One. 2023 Nov 8;18(11):e0293409. doi: 10.1371/journal.pone.0293409. eCollection 2023. PLoS One. 2023. PMID: 37939041 Free PMC article.
References
- Beaumont MA. Joint determination of topology, divergence time and immigration in population trees. In: Matsumura S, Forster P, Renfrew C, editors. Simulations, Genetics and Human Prehistory. Cambridge: (McDonald Institute Monographs), McDonald Institute for Archaeological Research; 2008. pp. 134–154.
- Bertorelle G, Excoffier L. Inferring admixture proportion from molecular data. Mol. Biol. Evol. 1998;15:1298–1311. - PubMed