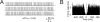Fast-reset of pacemaking and theta-frequency resonance patterns in cerebellar golgi cells: simulations of their impact in vivo - PubMed (original) (raw)
Fast-reset of pacemaking and theta-frequency resonance patterns in cerebellar golgi cells: simulations of their impact in vivo
Sergio Solinas et al. Front Cell Neurosci. 2007.
Abstract
The Golgi cells are inhibitory interneurons of the cerebellar granular layer, which respond to afferent stimulation in vivo with a burst-pause sequence interrupting their irregular background low-frequency firing (Vos et al., 1999a. Eur. J. Neurosci. 11, 2621-2634). However, Golgi cells in vitro are regular pacemakers (Forti et al., 2006. J. Physiol. 574, 711-729), raising the question how their ionic mechanisms could impact on responses during physiological activity. Using patch-clamp recordings in cerebellar slices we show that the pacemaker cycle can be suddenly reset by spikes, making the cell highly sensitive to input variations. Moreover, the neuron resonates around the pacemaker frequency, making it specifically sensitive to patterned stimulation in the theta-frequency band. Computational analysis based on a model developed to reproduce Golgi cell pacemaking (Solinas et al., 2008Front. Neurosci., 2:2) predicted that phase-reset required spike-triggered activation of SK channels and that resonance was sustained by a slow voltage-dependent potassium current and amplified by a persistent sodium current. Adding balanced synaptic noise to mimic the irregular discharge observed in vivo, we found that pacemaking converts into spontaneous irregular discharge, that phase-reset plays an important role in generating the burst-pause pattern evoked by sensory stimulation, and that repetitive stimulation at theta-frequency enhances the time-precision of spike coding in the burst. These results suggest that Golgi cell intrinsic properties exert a profound impact on time-dependent signal processing in the cerebellar granular layer.
Keywords: cerebellum; golgi cell; granular layer; modeling; phase-reset; resonance.
Figures
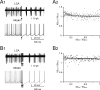
Figure 1
Phase reset of pacemaking. (A1 and B1) A Golgi cell recorded in LCA (black trace) shows autorhythmic firing when a single (A1) or four antidromic spikes at 50 Hz (B1) are elicited by axonal electrical stimulation (arrows). In different sweeps the stimulus was delivered at different phases of the pacemaker cycle. Nonetheless, following stimulation the Golgi cell is phase reset, i.e., restarts firing almost without memory of the preceding phase. The same behavior is observed in the model (gray traces) stimulated with 0.5 ms-long current pulses delivered at varying times during the ISI (the stimulus size is tuned as to inject the minimal charge required to elicit an AP according to the plot in Figure 2B). (A2 and B2) The plots show summary data from 13 and 6 Golgi cells, respectively, to which antidromic stimulation was applied. The time interval between the resetting stimuli and the subsequent spike (ISIpost ) is compared to the time interval preceding the stimulus (ISIpre). Both ISIpre and ISIpost were normalized by the average ISI of pacemaking (ISIpace). ISIpost /ISIpace was independent from ISIpre . With 1 stimulus (B1) the correlation coefficient was −0.11 (not significantly different from 0, p > 0.18, _t_-test; average ISIpost/ISIpace = 1.05). With four stimuli (B2) the correlation coefficient was 0.08 (not significantly different from 0, p > 0.7, _t_-test; average ISIpost /ISIpace = 1.15). In either case, the model (gray traces) predicted the experimental results (p > 0.1, _t_-test). The experimental data were fitted using a single exponential function (solid black trace, dashed black traces show the 95% confidence limits).
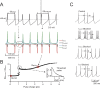
Figure 2
The mechanisms of phase-reset. (A) Phase-reset simulations were performed on subthreshold oscillations after blocking all voltage-dependent currents except for _I_Na-p, _I_CaHVA, _I_K-AHP, and _I_K-slow . The simulations show that small current pulses (2 nA for 0.5 ms) do not alter the cycle, while larger perturbations (6.8 nA for 0.5 ms) reset the cycle of the subthreshold oscillation. The currents involved are shown at the bottom, revealing that currents comparable to those observed during spikes are generated only with the larger pulse. (B) The same protocol used in A was repetitively applied to the model by varying pulse width (Δt = 0.1-3 ms) and amplitude (ΔI = 0.1-2 nA). The plot shows ISIpost-pre /ISIpace (cf. Figure 1) as a function of charge Q = ΔI · Δt. A sudden step in the plot indicates a sharp phase reset threshold. The EPSC and spike charges are also reported. The inset shows that one point in the plot corresponds to a hyperbolic trajectory in a stimulus strength-duration graph. (C) The phase-reset mechanism was explored by simulating block of specific ionic currents (control is with all ionic currents active, spikes are truncated for clarity). While in control simulations (upper trace) a spike-like perturbation resets the pacemaker phase, this does not occur after IK-AHP blockage (note that in this condition the model fires short spike bursts). However, blocking _I_K-slow or _I_K-A (lower traces) does not alter the phase reset. It should be noted that the absence of noise in these simulations prevented the ISI irregularity that would have been introduced by _I_K-AHP blockage in real cells (see Forti et al., ; Solinas et al., 2007).
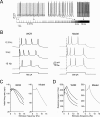
Figure 3
Intrinsic theta-frequency resonance. Intrinsic resonance was investigated by injecting short (40 ms) current steps at frequencies between 0.3 and 15 Hz. (A) A Golgi cell (WCR) in the pacemaking regime is repetitively driven to fire bursts of action potentials by injecting sequences of short (40 ms) current pulses. The pulses are repeated 10 times at each frequency (from 0.3 to 15 Hz). (B) Responses are intensified and show a shorter latency around 3 Hz. This experimental observation as also the resonance effects shown in panels C and D are reproduced by the model. (C) The initial firing rate (the inverse of the first ISI) is shown for three Golgi cell WCRs. The curves show resonance at 2.6 Hz. (D) The response speed (the inverse of first spike latency) is shown for the same three Golgi cells reported in C. The curves show resonance at around 3 Hz.
Figure 4
The mechanisms of resonance. (A) _I_K-AHP, _I_K-slow, and INa-p were measured in the model during the resonance protocol shown in Figure 3(the mean values of _I_K-AHP and _I_K-slow were measured over the inter-pulse interval, the mean value of _I_Na-p was measured over the first 5 ms of each depolarizing pulse). Note that _I_K-slow decreases while INa-p increases in the resonance region (since _I_Na-p has fast activation dynamics, its measure is disturbed by spikes) while _I_K-AHP increases linearly with frequency. (B) In model simulations, resonance could be explored in the immediate subthreshold range (−65 mV) after blocking spike mechanisms (_I_Na-t, _I_K-V, and _I_K-C ). The simulations show the ZAP response with all ionic current except for _I_K-slow and _I_Nap and after reintroducing _I_K-slow and _I_Na-p (50% for graphical reasons) in sequence. The corresponding impedance profiles are shown at the right. The simulations show that _I_K-slow generates and _I_Na-p amplifies resonance in the theta-frequency range.
Figure 5
The effect of noise on pacemaking. (A) Pacemaking in the model was perturbed by injecting random balanced synaptic currents causing a marked ISI irregularity. (B) The autocorrelogram of a 60-second long simulation shows that the random synaptic input cancels the regularity of the pacemaker cycle.
Figure 6
The effect of noise on phase-reset. (A) The model perturbed with balanced synaptic noise was stimulated by either 5-ms long or 30-ms long current pulses of 800 pA (lower traces show the stimulation protocols) to elicit a singlet or a triplet of spikes, respectively. Visual inspection shows an evident silent pause with the triplet but not with the singlet. (B) The PSTH for singlet shows a brief pause partly populated by spikes. The PSTH for triplets shows a pause roughly corresponding to the average pacemaker cycle free from any spikes. The insets show that the silent pause is short and unreliable with a singlet but not with a triplet. The bottom panel shows data recorded in vivo following vibrissal stimulation in the anaesthetized rat, which cause a brief spike sequence followed by a silent pause. Note the remarkable similarity between in vivo recordings and the model (triplet).
Figure 7
The effect of noise on resonance.(A) The resonance protocol reported in Figure 3 was also applied to the model perturbed with synaptic noise. The traces show the response to 800 pA current pulses taken from a sequence in which stimuli are delivered at increasing frequency. The traces at 6.2 Hz show greater precision of spike timing. (B) The plots show data from four simulations with different random seeds (there are four black circles for each tested stimulation frequency). The initial firing rate and the first spike delay do no longer show a clear resonance. However, the standard deviation of the first spike delay is clearly resonant with a peak at stimulation frequencies around 6 Hz.
Similar articles
- The critical role of Golgi cells in regulating spatio-temporal integration and plasticity at the cerebellum input stage.
D'Angelo E. D'Angelo E. Front Neurosci. 2008 Jul 7;2(1):35-46. doi: 10.3389/neuro.01.008.2008. eCollection 2008 Jul. Front Neurosci. 2008. PMID: 18982105 Free PMC article. - Computational reconstruction of pacemaking and intrinsic electroresponsiveness in cerebellar Golgi cells.
Solinas S, Forti L, Cesana E, Mapelli J, De Schutter E, D'Angelo E. Solinas S, et al. Front Cell Neurosci. 2007 Dec 30;1:2. doi: 10.3389/neuro.03.002.2007. eCollection 2007. Front Cell Neurosci. 2007. PMID: 18946520 Free PMC article. - The cerebellar Golgi cell and spatiotemporal organization of granular layer activity.
D'Angelo E, Solinas S, Mapelli J, Gandolfi D, Mapelli L, Prestori F. D'Angelo E, et al. Front Neural Circuits. 2013 May 17;7:93. doi: 10.3389/fncir.2013.00093. eCollection 2013. Front Neural Circuits. 2013. PMID: 23730271 Free PMC article. Review. - Determinants of rebound burst responses in rat cerebellar nuclear neurons to physiological stimuli.
Dykstra S, Engbers JD, Bartoletti TM, Turner RW. Dykstra S, et al. J Physiol. 2016 Feb 15;594(4):985-1003. doi: 10.1113/JP271894. Epub 2016 Jan 18. J Physiol. 2016. PMID: 26662168 Free PMC article. - Pacemaker neurons of the forebrain medical septal area and theta rhythm of the hippocampus.
Vinogradova OS, Kitchigina VF, Zenchenko CI. Vinogradova OS, et al. Membr Cell Biol. 1998;11(6):715-25. Membr Cell Biol. 1998. PMID: 9718568 Review.
Cited by
- The critical role of Golgi cells in regulating spatio-temporal integration and plasticity at the cerebellum input stage.
D'Angelo E. D'Angelo E. Front Neurosci. 2008 Jul 7;2(1):35-46. doi: 10.3389/neuro.01.008.2008. eCollection 2008 Jul. Front Neurosci. 2008. PMID: 18982105 Free PMC article. - Regulation of output spike patterns by phasic inhibition in cerebellar granule cells.
Nieus TR, Mapelli L, D'Angelo E. Nieus TR, et al. Front Cell Neurosci. 2014 Aug 25;8:246. doi: 10.3389/fncel.2014.00246. eCollection 2014. Front Cell Neurosci. 2014. PMID: 25202237 Free PMC article. - Neural circuit and its functional roles in cerebellar cortex.
Wang L, Liu SQ. Wang L, et al. Neurosci Bull. 2011 Jun;27(3):173-84. doi: 10.1007/s12264-011-1044-2. Neurosci Bull. 2011. PMID: 21614100 Free PMC article. - Back to front: cerebellar connections and interactions with the prefrontal cortex.
Watson TC, Becker N, Apps R, Jones MW. Watson TC, et al. Front Syst Neurosci. 2014 Feb 4;8:4. doi: 10.3389/fnsys.2014.00004. eCollection 2014. Front Syst Neurosci. 2014. PMID: 24550789 Free PMC article. - Sensory coding by cerebellar mossy fibres through inhibition-driven phase resetting and synchronisation.
Holtzman T, Jörntell H. Holtzman T, et al. PLoS One. 2011;6(10):e26503. doi: 10.1371/journal.pone.0026503. Epub 2011 Oct 26. PLoS One. 2011. PMID: 22046297 Free PMC article. Retracted.
References
- Buzsaki G. (2006). Rhythms of the brain (USA, Oxford University Press; ).
- Chadderton P., Margrie T. W., Häusser M. (2004). Integration of quanta in cerebellar granule cells during sensory processing. Nature 428, 856–860 - PubMed
- De Schutter E. (2002). Cerebellar cortex: computation by extrasynaptic inhibition. Curr. Biol. 12, R363–R365 - PubMed
- De Schutter E., Bjaalie J. G. (2001). Coding in the granular layer of the cerebellum. Prog. Brain Res. 130, 279–296 - PubMed
LinkOut - more resources
Full Text Sources
Molecular Biology Databases