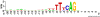Support vector machines and kernels for computational biology - PubMed (original) (raw)
Review
Support vector machines and kernels for computational biology
Asa Ben-Hur et al. PLoS Comput Biol. 2008 Oct.
No abstract available
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
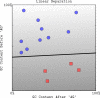
Figure 1. A linear classifier separating two classes of points (squares and circles) in two dimensions.
The decision boundary divides the space into two sets depending on the sign of f(x) = 〈w,x〉+b. The grayscale level represents the value of the discriminant function f(x): dark for low values and a light shade for high values.
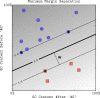
Figure 2. The maximum margin boundary computed by a linear SVM.
The region between the two thin lines defines the margin area with −1≤〈w,x〉+_b_≤1. The data points highlighted with black centers are the support vectors: the examples that are closest to the decision boundary. They determine the margin by which the two classes are separated. Here, there are three support vectors on the edge of the margin area (f(x) = −1 or f(x) = +1).
Figure 3. The effect of the soft-margin constant, C, on the decision boundary.
We modified the toy dataset by moving the point shaded in gray to a new position indicated by an arrow, which significantly reduces the margin with which a hard-margin SVM can separate the data. (A) We show the margin and decision boundary for an SVM with a very high value of C, which mimics the behavior of the hard-margin SVM since it implies that the slack variables ξi (and hence training mistakes) have very high cost. (B) A smaller value of C allows us to ignore points close to the boundary, and increases the margin. The decision boundary between negative examples and positive examples is shown as a thick line. The thin lines are on the margin (discriminant value equal to −1 or +1).
Figure 4. The major steps in protein synthesis: transcription, post-processing, and translation.
In the post-processing step, the pre-mRNA is transformed into mRNA. One necessary step in the process of obtaining mature mRNA is called splicing. The mRNA sequence of a eukaryotic gene is “interrupted” by noncoding regions called introns. A gene starts with an exon and may then be interrupted by an intron, followed by another exon, intron, and so on until it ends in an exon. In the splicing process, the introns are removed. There are two different splice sites: the exon–intron boundary, referred to as the donor site or 5′ site (of the intron), and the intron–exon boundary, that is, the acceptor or 3′ site. Splice sites have quite strong consensus sequences, i.e., almost every position in a small window around the splice site is representative of the most frequently occurring nucleotide when many existing sequences are compared in an alignment (cf. Figure 5). (The caption text appeared similarly in , the idea for this figure is from .)
Figure 5. Sequence logo for acceptor splice sites: splice sites have quite strong consensus sequences, i.e., almost every position in a small window around the splice site is representative of the most frequently occurring nucleotide when many existing sequences are compared in an alignment.
The sequence logo , shows the region around the intron/exon boundary—the acceptor splice site. In the running example, we use the region up to 40 nt upstream and downstream of the consensus site AG.
Figure 6. The effect of the degree of a polynomial kernel.
The polynomial kernel of degree 1 leads to a linear separation (A). Higher-degree polynomial kernels allow a more flexible decision boundary (B,C). The style follows that of Figure 3.
Figure 7. The effect of the width parameter of the Gaussian kernel (σ) for a fixed value of the soft-margin constant.
For large values of σ (A), the decision boundary is nearly linear. As σ decreases, the flexibility of the decision boundary increases (B). Small values of σ lead to overfitting (C). The figure style follows that of Figure 3.
Similar articles
- Guest editors' introduction to the special section on syntactic and structural pattern recognition.
Basu M, Bunke H, Del Bimbo A. Basu M, et al. IEEE Trans Pattern Anal Mach Intell. 2005 Jul;27(7):1009-12. doi: 10.1109/TPAMI.2005.141. IEEE Trans Pattern Anal Mach Intell. 2005. PMID: 16013749 No abstract available. - A convex approach to validation-based learning of the regularization constant.
Pelckmans K, Suykens JA, De Moor B. Pelckmans K, et al. IEEE Trans Neural Netw. 2007 May;18(3):917-20. doi: 10.1109/TNN.2007.891187. IEEE Trans Neural Netw. 2007. PMID: 17526357 - Information criteria for support vector machines.
Kobayashi K, Komaki F. Kobayashi K, et al. IEEE Trans Neural Netw. 2006 May;17(3):571-7. doi: 10.1109/TNN.2006.873276. IEEE Trans Neural Netw. 2006. PMID: 16722163 - Machine learning techniques to examine large patient databases.
Meyfroidt G, Güiza F, Ramon J, Bruynooghe M. Meyfroidt G, et al. Best Pract Res Clin Anaesthesiol. 2009 Mar;23(1):127-43. doi: 10.1016/j.bpa.2008.09.003. Best Pract Res Clin Anaesthesiol. 2009. PMID: 19449621 Review. - Creation of reliable relevance judgments in information retrieval systems evaluation experimentation through crowdsourcing: a review.
Samimi P, Ravana SD. Samimi P, et al. ScientificWorldJournal. 2014;2014:135641. doi: 10.1155/2014/135641. Epub 2014 May 19. ScientificWorldJournal. 2014. PMID: 24977172 Free PMC article. Review.
Cited by
- Decoding lifespan changes of the human brain using resting-state functional connectivity MRI.
Wang L, Su L, Shen H, Hu D. Wang L, et al. PLoS One. 2012;7(8):e44530. doi: 10.1371/journal.pone.0044530. Epub 2012 Aug 30. PLoS One. 2012. PMID: 22952990 Free PMC article. - Machine learning: A powerful tool for gene function prediction in plants.
Mahood EH, Kruse LH, Moghe GD. Mahood EH, et al. Appl Plant Sci. 2020 Jul 28;8(7):e11376. doi: 10.1002/aps3.11376. eCollection 2020 Jul. Appl Plant Sci. 2020. PMID: 32765975 Free PMC article. Review. - Inferring genome-wide patterns of admixture in Qataris using fifty-five ancestral populations.
Omberg L, Salit J, Hackett N, Fuller J, Matthew R, Chouchane L, Rodriguez-Flores JL, Bustamante C, Crystal RG, Mezey JG. Omberg L, et al. BMC Genet. 2012 Jun 26;13:49. doi: 10.1186/1471-2156-13-49. BMC Genet. 2012. PMID: 22734698 Free PMC article. - Harnessing the power of machine learning for crop improvement and sustainable production.
Khatibi SMH, Ali J. Khatibi SMH, et al. Front Plant Sci. 2024 Aug 12;15:1417912. doi: 10.3389/fpls.2024.1417912. eCollection 2024. Front Plant Sci. 2024. PMID: 39188546 Free PMC article. Review. - FaaPred: a SVM-based prediction method for fungal adhesins and adhesin-like proteins.
Ramana J, Gupta D. Ramana J, et al. PLoS One. 2010 Mar 15;5(3):e9695. doi: 10.1371/journal.pone.0009695. PLoS One. 2010. PMID: 20300572 Free PMC article.
References
- Boser BE, Guyon IM, Vapnik VN. A training algorithm for optimal margin classifiers. In: Haussler D, editor. 5th Annual ACM Workshop on COLT. Pittsburgh (Pennsylvania): ACM Press; 1992. pp. 144–152. Available: http://www.clopinet.com/isabelle/Papers. Accessed 11 August 2008.
- Schölkopf B, Smola A. Learning with kernels. Cambridge (Massachusetts): MIT Press; 2002.
- Vapnik V. The nature of statistical learning theory. 2nd edition. Springer; 1999.
- Müller KR, Mika S, Rätsch G, Tsuda K, Schölkopf B. An introduction to kernel-based learning algorithms. IEEE Trans Neural Netw. 2001;12:181–201. - PubMed
- Schölkopf B, Tsuda K, Vert JP. Kernel methods in computational biology. Cambridge (Massachusetts): MIT Press; 2004.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources