Facilitated variation: how evolution learns from past environments to generalize to new environments - PubMed (original) (raw)

Facilitated variation: how evolution learns from past environments to generalize to new environments

Merav Parter et al. PLoS Comput Biol. 2008 Nov.

Abstract

One of the striking features of evolution is the appearance of novel structures in organisms. Recently, Kirschner and Gerhart have integrated discoveries in evolution, genetics, and developmental biology to form a theory of facilitated variation (FV). The key observation is that organisms are designed such that random genetic changes are channeled in phenotypic directions that are potentially useful. An open question is how FV spontaneously emerges during evolution. Here, we address this by means of computer simulations of two well-studied model systems, logic circuits and RNA secondary structure. We find that evolution of FV is enhanced in environments that change from time to time in a systematic way: the varying environments are made of the same set of subgoals but in different combinations. We find that organisms that evolve under such varying goals not only remember their history but also generalize to future environments, exhibiting high adaptability to novel goals. Rapid adaptation is seen to goals composed of the same subgoals in novel combinations, and to goals where one of the subgoals was never seen in the history of the organism. The mechanisms for such enhanced generation of novelty (generalization) are analyzed, as is the way that organisms store information in their genomes about their past environments. Elements of facilitated variation theory, such as weak regulatory linkage, modularity, and reduced pleiotropy of mutations, evolve spontaneously under these conditions. Thus, environments that change in a systematic, modular fashion seem to promote facilitated variation and allow evolution to generalize to novel conditions.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Figure 1

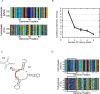
Figure 1. A small number of mutations evokes large useful phenotypic adaptation in systems showing facilitated variation.

(A) Beaks of Darwin's finches. (B) RNA secondary structure evolved under modularly varying goals (MVG). (C) Logic circuit evolved under MVG of decomposable Boolean functions.

Figure 2

Figure 2. Schematic view of evolutionary goals and phenotypes in the two model systems.

(A–B) Logic circuit model. (A) A typical circuit evolved by fixed-goal evolution toward goal G1. Each gate in the circuit represents a NAND gate. (B) Modular circuit evolved under modularly varying goal evolution with goals G1-G3. The circuit is composed of two XOR modules that input into a third module which implements the OR function. Each goal has four inputs and one output of the form G(x,y,w,z) = f(g(x,y),h(w,z)). During evolution, goal switches over time in probabilistic manner as a random walk on the graph in this figure; Note that in every switch, a single XOR module is changed to EQ, and vice versa. (C) RNA model, goal G1 is the secondary structure of a natural tRNA, goals G2, G3 and G4 are modular variants of G1, in which one hairpin loop is replaced by an open loop. The goal switches during evolution in a probabilistic manner as a random walk on the graph in the figure. Note that in every switch, a single hairpin is changed to an open loop and vice-versa.

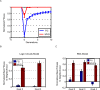
Figure 3

Figure 3. MVG-evolved organisms adapt faster than fixed-goal organisms when goals change.

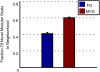
(A) Adaptation following a goal switch (logic circuit model). The x-axis denotes generations, where zero is the point where the goal changes to a new goal (a previously seen goal in the case of MVG). Maximal normalized fitness in the population at each time point (mean±SE) is shown. Initial populations are FG-populations evolved toward G1 and MVG-populations taken from the end of the last G1-epoch. The new goals were G2 = (x EQ y) OR (w XOR z) and G3 = (x XOR y) OR (w EQ z). Data are from 30 simulations for each scenario. (B) Maximal normalized fitness (mean±SE) for past goal G≠G1 in the genetic neighborhood of evolved logic circuits. (C) Same as in (B) but for evolved RNA genomes. The genetic neighborhood is defined as the set of all genomes different in one position from the wild type genomes.

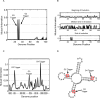
Figure 4

Figure 4. Evolution of genetic triggers.

(A) Mutual information (y-axis) between the environment (goal) and the genomic content at each position of an evolved MVG circuit (x-axis). Two positions (positions 28 and 31) have high mutual information and are defined as genetic triggers which facilitate circuit's adaptation for goals G3 and G2 respectively. (B) Same as in (A), but at three time points along evolution: beginning, middle and end of evolution. (C) as in (A), but for the RNA model. The x-axis is labeled with the parenthesis notation for RNA secondary structure. (D) Genetic triggers of (C) placed on the structure of the evolved MVG RNA molecule.

Figure 5

Figure 5. Schematic representation of MVG ‘modularity language’.

(A) Logic circuit model, goals within MVG language are of the form u(x,y,w,z) = f(g(x,y), h(w,z)). (B) RNA model, goals within MVG language are structures with independent structural modules that correspond in their genomic positions to MVG module.

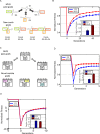
Figure 6

Figure 6. Adaptation towards novel modular goals is more rapid in MVG organisms.

(A) An example of new-comb goal in the RNA model, where the new goal structure is composed of previously seen sub-structures but in new combinations. (B) Maximal normalized fitness in RNA populations (mean±SE) as a function of generations for new-comb structures. The x-axis is generations, where zero is the point where the goal changes to a new-comb structure. Initial populations are FG-populations evolved toward G1 and MVG populations taken from the end of the last G1-epoch. Data are from 15 simulations for the four new-comb goals of (A). Inset: competition of FG and MVG populations under a new-comb goal (following the method of [44]). Initial populations were composed of equal fractions of FG-populations and MVG populations. Data are from 30 competition runs for each of the four new-comb goals. (C) Novel-module goal in the logic circuit model. In the novel-module goal, one of the 2 XORs or the OR operation was changed into a different 2-inputs Boolean function such as AND, NOR or XOR, not seen in the history of the evolution. (D) Maximal normalized fitness (mean±SE) as a function of generations for novel-module goals in the logic circuit model. At time zero the goal changes to a novel-module goal. Initial populations are as in (B). Data are from 30 simulations in each scenario, for 20 different novel-module goals (listed in Text S1 section 6.4.2). Inset: Competition of FG and MVG organisms in a novel-module environment. Starting populations were composed of equal fractions of FG and MVG populations. Data are from 30 simulations for 20 novel-module goals. (E) Same as in (D) but for non-MVG language goals. Here, the goal is a randomly chosen Boolean function, generated by randomly generating a 4-input 1-output truth table. Goals with a difficulty level similar to that of (D) were chosen, as evaluated (Text S1 section 6.2). Data are for 35 non-MVG language goals. Inset: Competition results as in the inset of (D).

Figure 7

Figure 7. Reduction in genetic variance in MVG evolution.

(A) Genomes of evolved RNA populations under FG and MVG scenarios. Each row corresponds to a 76-nucleotide genome of an individual in the population. Color stands for the genomic position content (A,U,G,C). For MVG, the end of the last G1-epoch population is presented. (B) Conditional genomic entropy (mean±SE) as a function of number of goals presented along MVG evolution (x-axis). (C) FG scenario was toward G1. In MVG the goal switched repeatedly between G1 and G2. G2 is a modular variation of G1 with hairpin instead of an open loop in a module corresponding to genomic positions 7 to 26. (D) Genomes of evolved RNA populations with FG and MVG scenarios as described in (C). Note the low variance in MVG populations within the marked region, which corresponds to the genomic positions of the loop region that varies between goals.

Figure 8

Figure 8. Enrichment of phenotypic neighborhood of logic circuits with novel ‘useful’ phenotypes.

Number of novel modular functions divided by the number of all novel functions found in the phenotypic neighborhood of an evolved circuit is shown. Mean±SE is presented for best individuals in MVG and FG populations. Goals were: G1 = (x XOR y) OR (w XOR z), G2 = (x XOR y) AND (w XOR z). For MVG, data are for generations where the goal was G1. Data are from 40 simulations in each case.

Figure 9

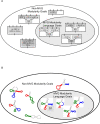
Figure 9. Dynamics of facilitated variation.

(A) Schematic presentation of a phenotypic neighborhood with high facilitated variation. Outer ellipse is the phenotypic space, inner ellipses stand for non-trivial Boolean functions that are within (right ellipse), or without the MVG modularity language (left ellipse), P0 is the wild-type phenotype and P1–10 are neighboring phenotypes. The thickness of the arrow represents the probability of the wild-type to generate Pi with one genetic mutation. Length of an edge represents the distance of the phenotypic ‘jump’. High FV corresponds to many long and thick arrows towards the right ellipse. (B) Facilitated variation measure (mean±SE) in RNA model of MVG, FG and a random class of inverse-fold genomes (genomes generated by an algorithm to yield a desired fold) with G1 structure. Data are from 30 simulations in the case of FG and MVG and 200 random genomes. (C) Facilitated variation measure (mean±SE) as a function of generations in logic circuits evolution. Goals were: G1 = (x XOR y) OR (w XOR z), G2 = (x XOR y) AND (w XOR z). For MVG, data are for generations where the goal was G1. Data are from 40 simulations in each case. The random class (dashed line) includes circuits which achieve the goal but were generated by an optimization algorithm rather than by an evolutionary process (see Text S1 section 3.1). (D) Facilitated variation rapidly decays when goal becomes constant over time. Each simulation started from end-of MVG evolution population that had perfect fitness for the goal G1.At the generation marked zero, the population was placed under a FG evolution with the same goal G1, with a selection pressure for minimizing the number of gates (fitness reduction of 0.2/gate for each gate over 10 gates). Mean FV measure (±SE) vs. generations of 500 best-fitness circuits in each population is shown. Statistics are for 30 independent experiments.

Similar articles

Cited by

References

    1. Baldwin M. A New Factor in Evolution. The American Naturalist. 1896;30:441–451.
    1. Simpson G. The Baldwin effect. Evolution. 1953;7:110–117.
    1. Waddington CH. Canalization of development and genetic assimilation of acquired characters. Nature. 1959;183:1654–1655. - PubMed
    1. Waddington CH. Genetic assimilation. Adv Genet. 1961;10:257–293. - PubMed
    1. Kirschner M, Gerhart JC. The Plausibility of Life. London (United Kingdom: Yale University Press; 2005.

Publication types

MeSH terms

Substances

LinkOut - more resources