Practical issues in imputation-based association mapping - PubMed (original) (raw)
Practical issues in imputation-based association mapping
Yongtao Guan et al. PLoS Genet. 2008 Dec.
Abstract
Imputation-based association methods provide a powerful framework for testing untyped variants for association with phenotypes and for combining results from multiple studies that use different genotyping platforms. Here, we consider several issues that arise when applying these methods in practice, including: (i) factors affecting imputation accuracy, including choice of reference panel; (ii) the effects of imputation accuracy on power to detect associations; (iii) the relative merits of Bayesian and frequentist approaches to testing imputed genotypes for association with phenotype; and (iv) how to quickly and accurately compute Bayes factors for testing imputed SNPs. We find that imputation-based methods can be robust to imputation accuracy and can improve power to detect associations, even when average imputation accuracy is poor. We explain how ranking SNPs for association by a standard likelihood ratio test gives the same results as a Bayesian procedure that uses an unnatural prior assumption--specifically, that difficult-to-impute SNPs tend to have larger effects--and assess the power gained from using a Bayesian approach that does not make this assumption. Within the Bayesian framework, we find that good approximations to a full analysis can be achieved by simply replacing unknown genotypes with a point estimate--their posterior mean. This approximation considerably reduces computational expense compared with published sampling-based approaches, and the methods we present are practical on a genome-wide scale with very modest computational resources (e.g., a single desktop computer). The approximation also facilitates combining information across studies, using only summary data for each SNP. Methods discussed here are implemented in the software package BIMBAM, which is available from http://stephenslab.uchicago.edu/software.html.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
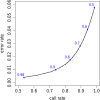
Figure 1. Graph showing the trade-off between call-rate and error rate, as the probability threshold for calling an imputed genotype is varied.
Numbers along the line indicate the thresholds that produce the corresponding call rate and error rate; small black points indicate results for intermediate thresholds in increments of 0.02. For example, if we call only those imputed genotypes assigned probability >0.9 of being correct, then approximately 74% of imputed genotypes are called, and of these called genotypes approximately 1% are incorrect.
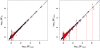
Figure 2. Graphs showing correspondence of BFmean (_x_-axis) vs BFIS (_y_-axis on left panel) and BFnaive (_y_-axis on right panel).
In each case the diagonal blue line is y = x, and the vertical red lines indicate ±2 standard errors of the Bayes factor estimate (for example, on the left they run between log10(BFIS±2 standard errors)).
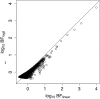
Figure 3. Graph showing correspondance between log10(BFmean) values and Likelihood ratio statistics Λ (left) and Λmean (right).
Each point represents one SNP-phenotype combination, colored according to average confidence in imputed genotypes. Specifically, the SNPs were colored according to the value of r, defined to be the ratio of the variance of the (posterior mean) genotypes and the expected variance if the SNP were typed, calculated from the MAF assuming Hardy-Weinberg equilibrium (2_f_(1−f)). This scaling ensures that for typed and confidently-imputed SNPs _r_≈1, whereas for SNPs with low average confidence r will be close to 0. Colors indicate ranges of values of r: red _r_∈(0,0.001]; green _r_∈(0.001,0.01]; blue _r_∈(0.01,0.1]; cyan _r_∈(0.1,0.5]; black _r_>0.5.
Figure 4. Effects of different test statistics on power to detect associations.
Each line shows the trade-off between true and false discoveries when using Bayes factors (black lines) or likelihood ratio test statistics Λ (red solid lines) and Λmean (red dashed lines), as threshold for declaring an association is varied. In each setting the Bayes factor produces as good, or better, performance than the likelihood ratio test (black lines are above the corresponding red lines). Best performance is obtained using CEU panel, which is well-matched to the sample and produces a low imputation error rate (left; imputation error rate 6.2%). Larger increases in imputation error rate, obtained when using YRI panel that is not well-matched to sample, produce a notable reduction in performance (right; imputation error rate 25%). However, even with a high imputation error rate, using the Bayes factor as a test statistic gives better results than no imputation (blue dotted lines in both panel).
Figure 5. The x-axis is log10 (BF) of linear model and y-axis is log10 BF of logistic model.
The blue line is x = y.
Similar articles
- Accuracy of genome-wide imputation of untyped markers and impacts on statistical power for association studies.
Hao K, Chudin E, McElwee J, Schadt EE. Hao K, et al. BMC Genet. 2009 Jun 16;10:27. doi: 10.1186/1471-2156-10-27. BMC Genet. 2009. PMID: 19531258 Free PMC article. - Imputation-based analysis of association studies: candidate regions and quantitative traits.
Servin B, Stephens M. Servin B, et al. PLoS Genet. 2007 Jul;3(7):e114. doi: 10.1371/journal.pgen.0030114. Epub 2007 May 30. PLoS Genet. 2007. PMID: 17676998 Free PMC article. - Analysis of untyped SNPs: maximum likelihood and imputation methods.
Hu YJ, Lin DY. Hu YJ, et al. Genet Epidemiol. 2010 Dec;34(8):803-15. doi: 10.1002/gepi.20527. Genet Epidemiol. 2010. PMID: 21104886 Free PMC article. - Genotype Imputation from Large Reference Panels.
Das S, Abecasis GR, Browning BL. Das S, et al. Annu Rev Genomics Hum Genet. 2018 Aug 31;19:73-96. doi: 10.1146/annurev-genom-083117-021602. Epub 2018 May 23. Annu Rev Genomics Hum Genet. 2018. PMID: 29799802 Review. - Accurate Imputation of Untyped Variants from Deep Sequencing Data.
Torkamaneh D, Belzile F. Torkamaneh D, et al. Methods Mol Biol. 2021;2243:271-281. doi: 10.1007/978-1-0716-1103-6_13. Methods Mol Biol. 2021. PMID: 33606262 Review.
Cited by
- The Bayesian lens and Bayesian blinkers.
Stephens M. Stephens M. Philos Trans A Math Phys Eng Sci. 2023 May 15;381(2247):20220144. doi: 10.1098/rsta.2022.0144. Epub 2023 Mar 27. Philos Trans A Math Phys Eng Sci. 2023. PMID: 36970830 Free PMC article. Review. - False positive findings during genome-wide association studies with imputation: influence of allele frequency and imputation accuracy.
Zhang Z, Xiao X, Zhou W, Zhu D, Amos CI. Zhang Z, et al. Hum Mol Genet. 2021 Dec 17;31(1):146-155. doi: 10.1093/hmg/ddab203. Hum Mol Genet. 2021. PMID: 34368847 Free PMC article. - Impact of pre- and post-variant filtration strategies on imputation.
Charon C, Allodji R, Meyer V, Deleuze JF. Charon C, et al. Sci Rep. 2021 Mar 18;11(1):6214. doi: 10.1038/s41598-021-85333-z. Sci Rep. 2021. PMID: 33737531 Free PMC article. - Why are rare variants hard to impute? Coalescent models reveal theoretical limits in existing algorithms.
Si Y, Vanderwerff B, Zöllner S. Si Y, et al. Genetics. 2021 Apr 15;217(4):iyab011. doi: 10.1093/genetics/iyab011. Genetics. 2021. PMID: 33686438 Free PMC article. - Testing and controlling for horizontal pleiotropy with probabilistic Mendelian randomization in transcriptome-wide association studies.
Yuan Z, Zhu H, Zeng P, Yang S, Sun S, Yang C, Liu J, Zhou X. Yuan Z, et al. Nat Commun. 2020 Jul 31;11(1):3861. doi: 10.1038/s41467-020-17668-6. Nat Commun. 2020. PMID: 32737316 Free PMC article.
References
- Marchini J, Howie B, Myers S, McVean G, Donnelly P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat Genet. 2007;39:906–913. - PubMed
Publication types
MeSH terms
Grants and funding
- HG02585/HG/NHGRI NIH HHS/United States
- U01 HL084689/HL/NHLBI NIH HHS/United States
- R01 HG002585/HG/NHGRI NIH HHS/United States
- HL084689/HL/NHLBI NIH HHS/United States
- U01 HL069757/HL/NHLBI NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources